الرياضيات للشعب العلمية والتكنولوجية 2016 الدورة العادية: التصحيح
|
الشعبة : |
العلوم التجريبية |
السنة : |
2016 |
|
المسلك : |
العلوم الفيزيائية |
الدورة : |
العادية |
|
المادة : |
الرياضيات |
المدة : |
3 ساعات |
التمرين الأول: المتتاليات العددية
لیكن من لدينا:
* بين بالترجع أن لكل من
لیكن من
نفترض أن ولنبين أن
لدينا
ولدينا
الخلاصة:
لدينا
أي
إذن متتالیة ھندسیة أساسھا
ولدينا
الخلاصة:
لیكن من
لنكتب بدلالة
لدينا
لدينا
التمرين الثاني: الهندسة الفضائية
لدينا و
إذن
لدينا منظمية على
إذن معادلة المستوى تكتب على شكل
ولدينا إذن
الخلاصة: هي معادلة ديكارتية للمستوى
لتكن نقطة من الفضاء
لدينا
الخلاصة: مركز الفلكة هو النقطة وشعاعها هو
لدينا
وبما أن فإن المستوى يقطع الفلكة وفق دائرة
لدينا منظمية على
بما أن فإن موجهة للمستقيم
ولدينا
إذن التمثيل البارامتري للمستقيم هو
مركز الدائرة هو المسقط العمودي للنقطة على المستوى ، أي نقطة تقاطع و
بتعویض إحداثیات في التمثیل البارامیتري للمستقیم نجد:
ولدينا
الخلاصة:
التمرين الثالث: الأعداد العقدية
مميز المعادلة هو
إذن للمعادلة حلان مترافقان هما:
الخلاصة:
لدينا
ومنه
بما أن مرافق فإن
لدينا
ولدينا و
إذن
ولدينا
لدينا
وبالتالي صورة النقطة بالدوران الذي مركزه وزاويته هي النقطة
التمرين الرابع: حساب الاحتمالات
نسحب عشوائيا وفي آن واحد كرتين من الصندوق
إذن كل نتیجة للتجربة ھي تأليفة لعنصرین من بین عناصر ومنه
الحدث : “الكرتان المسحوبتان حمراوان”
إذن
الخلاصة:
ليكن المتغير العشوائي الذي يربط كل سحبة بعدد الكرات الحمراء المتبقية في الصندوق بعد سحب الكرتين
قيم هي:
- عند سحب كرتين حمراوتين
- عند سحب كرة حمراء وكرة خضراء
- عند سحب كرتين خضراوتين
إذن مجموعة القيم التي يأخذها المتغير العشوائي هي
الحدث يعني سحب كرة حمراء وكرة خضراء
إذن
ومنه
ولدينا و
الخلاصة: قانون احتمال هو
مسألة: دراسة دالة عددية وحساب التكامل
لدينا
إذن
لدينا
إذن المستقيم الذي معادلته مقارب للمنحنى بجوار
لدينا
إذن
لدينا
هندسيا يقبل فرعا شلجميا في إتجاه محور الأراتيب بجوار
لیكن من
لدينا
ولدينا
جدول التغیرات:
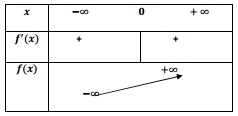
الدالة متصلة وتزايدية قطعا على
إذن المعادلة تقبل حلا وحيدا في حسب مبرهنة القيم الوسطية
ومنه يوجد عدد حقيقي وحيد من المجال بحيث
لیكن من
لدينا
وبما أن فإن إشارة هي إشارة
ولدينا
إذن
وبالتالي يوجد فوق المستقيم على المجال
ولدينا
إذن يوجد تحت المستقيم على المجال
لدينا
ولدينا
و
بما أن تنعدم في مع تغير إشارتها فإن نقطة انعطاف
إنشاء
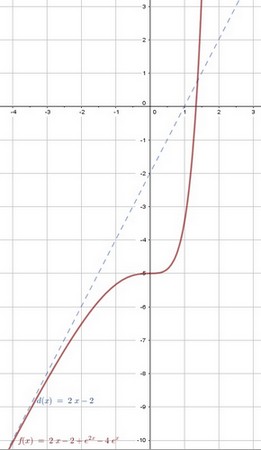
لدينا
المساحة هي:
المعادلة المميزة ب هي:
لدينا
إذن حلول هي الدوال المعرفة بما يلي:
ليكن حل المعادلة الذي يحقق الشرطين و
لدينا
الخلاصة:
الدالة قابلة للاشتقاق على
ولدينا
إذن الدالة قابلة للاشتقاق على ومشتقتها هي:
بما أن فإن و أي


