الامتحان الوطني الموحد 2015 الدورة الإستدراكية: الموضوع والتصحيح

1
التمرين 1
الكيمياء: التحولات الكيميائية لمجموعة

توظف النكهات بكثرة في الصناعة الغذائية، وتعزى إلى وجود مركبات طبيعية أو مصنعة مثل بوتانوات الإثيل ذي نكهة الأناناس وبوتانوات الإيزوأميل ذي نكهة الإجاص وبوتانوات المثيل ذي نكهة التفاح

يهدف هذا التمرين إلى دراسة التطور الزمني لمجموعة كيميائية تحتوي على بوتانوات المثيل وتحديد ثابتة الحمضية لمزدوجة الحمض الكربوكسيلي المستعمل في تحضيره

الجزء الأول: التطور الزمني لمجموعة كيميائية

نحضر بوتانوات المثيل $C H_{3} C H_{2} C H_{2} C O O C H_{3}$ بتفاعل حمض كربوكسيلي $A$ وكحول $B$

ننمذج هذا التفاعل بالمعادلة الكيميائية:

$A_{(l)} + B_{(l)} ⇌ C H_{3} C H_{2} C H_{2} C O O C {H_{3}}_{(l)} + H_{2} O_{(l)}$

$1$ أعط اسم المجموعة العضوية التي ينتمي إليها بوتانوات المثيل

$2$ استنتج الصيغة نصف المنشورة لكل من الحمض الكربوكسيلي $A$ والكحول $B$

$3$ أعط مميزتي هذا التفاعل

$4$ ننجز هذا التفاعل تحت درجة حرارة ثابتة $25 ° C$ حيث تحتوي المجموعة الكيميائية في الحالة البدئية على $n_{0} (A) = 1 m o l$ و $n_{0} (B) = 1 m o l$

حجم المجموعة الكيميائية يبقى ثابتا ويساوي: $V = 132 m L$

$1 - 4$ أنشئ الجدول الوصفي لتقدم التفاعل

$2 - 4$ مكنت الدراسة التجريبية من تتبع تطور كمية مادة الإستر المتكون وكمية مادة الحمض الكربوكسيلي $A$ المتبقي كما يبين الشكل جانبه

عين، معللا جوابك، من بين المنحنيين 1 و2، المنحنى الممثل لتغيرات كمية مادة الإستر

$3 - 4$ أوجد قيمة مردود التفاعل

$4 - 4$ كيف يمكن تحسين مردود هذا التفاعل؟

$5 - 4$ اُحسب بالوحدة $m o l . L^{- 1} . m i n^{- 1}$ قيمة السرعة الحجمية للتفاعل عند اللحظة $t = 0$

$6 - 4$ عين مبيانيا قيمة $t_{1 / 2}$ زمن نصف التفاعل

الجزء الثاني: تحديد ثابتة الحمضية لمزدوجة الحمض الكربوكسيلي $A$

نعتبر محلولا مائيا $(S_{A})$ للحمض الكربوكسيلي $A$ الذي نرمز له بالصيغة المبسطة $H A$ ،تركيزه المولي $C_{A}$ وحجمه $V_{0}$

$1$ لتحديد قيمة $C_{A}$ نعاير الحجم $V_{A} = 20 m L$ من المحلول $(S_{A})$ بواسطة محلول مائي $(S_{B})$ لهيدروكسيد الصوديوم $N a^{+} (a q) + H O^{-} (a q)$ تركيزه المولي $C_{B} = 2 . 10^{- 2} m o l . L^{- 1}$

$1 - 1$ اُكتب معادلة التفاعل الحاصل أثناء المعايرة والذي نعتبره كليا

$2 - 1$ حجم المحلول $(S_{B})$ المضاف عند التكافؤ هو: $V_{B E} = 10 m L$ . أوجد قيمة $C_{A}$

$2$ أعطى قياس $p H$ المحلول $(S_{A})$ عند درجة الحرارة $25 ° C$ القيمة $p H = 3, 4$ .

أوجد قيمة $K_{A}$ ثابتة الحمضية للمزدوجة $H A (a q) / A^{-} (a q)$

الكيمياء: التحولات الكيميائية لمجموعة

الجزء الأول: التطور الزمني لمجموعة كيميائية

$1$ اسم المجموعة العضوية التي ينتمي إليها بوتانوات الميثيل هو الاستر

$2$ الصيغة نصف المنشورة للحمض والكحول:

$3$ مميزات هذا التفاعل:

تفاعل محدود

تفاعل بطيء

$4$

$1 - 4$ الجدول الوصفي لتقدم التفاعل:

$2 - 4$ كمية مادة الاستر الناتج تتزايد مع مرور الزمن كما أن عند اللحظة $t = 0$ لدينا $n_{0} (E) = 0$

ومنه المنحنى $1$ يوافق تغيرات كمية مادة الاستر

$3 - 4$ مردود التفاعل يعبرعنه بالعلاقة: $r = \frac{n_{e x p}}{n_{m a x}}$

مبيانيا كمية مادة الاستر الناتجة عند نهاية التفاعل هي: $n_{f} = n_{e x p} = 0, 66 m o l$

كمية مادة الاستر الناتجة إذا كان التفاعل كليا: $n_{m a x} = n_{0} = 1 m o l$

$r = \frac{0, 66}{1} = 0, 66 = 66 %$

$4 - 4$ تحسين مردود تفاعل الاسترة:

إزالة الماء

استعمال أحد المتفاعلين بوفرة (الكحول أو الحمض)

$5 - 4$ حساب السرعة اللحظة عند اللحظة $t = 0$ :

حسب تعبير السرعة اللحظية:

$v (t = 0) = \frac{1}{V} . {(\frac{d x}{d t})}_{t = 0} v (t = 0) = \frac{1}{132 . 10^{- 3 l}} \times \frac{(0, 4 - 0) m o l}{(30 \times 7, 5 - 0) m i n} v (t = 0) = 1, 35 . 10^{- 2} m o l . l^{- 1} . m i n^{- 1}$

$6 - 4$ التعيين المبياني لـ $t_{1 / 2}$ من نصف التفاعل:

عند اللحظة $t_{1 / 2}$ يأخذ تقدم التفاعل نصف قيمته النهائية أي: $x (t_{1 / 2}) = 0, 33 m o l$ نجد مبيانيا:

$t_{1 / 2} = 210 \min$

الجزء الثاني: تحديد ثابتة الحمضية للحمض الكربوكسيلي $H A$

$1$

$1 - 1$ معادلة تفاعل المعايرة:

$H A_{(a q)} + H {O^{-}}_{(a q)} \to {A^{-}}_{(a q)} + H_{2} O_{(l)}$

$2 - 1$ قيمة التركيز $C_{A}$ :

علاقة التكافؤ: $C_{A} . V_{A} = C_{B} . V_{B E}$

ومنه:

$C_{A} = \frac{C_{B} . V_{B E}}{V_{A}}$

ت.ع:

$C_{A} = \frac{2 . 10^{- 2} \times 10}{20} = 1 . 10^{- 2} m o l . l^{- 2}$

$2$ قيمة الثابتة $K_{A}$ ثابتة الحمضية للمزدوجة: $H A_{(a q)} / {A^{-}}_{(a q)}$

تعبير $K_{A}$ هو

$K_{A} = \frac{{[H C O O^{-}]}_{é q} {[H_{3} O^{+}]}_{é q}}{{[H C O O H]}_{é q}}$

مع:

$\{\begin{cases} {[H C O O^{-}]}_{é q} = {[H_{3} O^{+}]}_{é q} \\ {[H C O O H]}_{é q} = \frac{C_{A} . V - x_{é q}}{V} = C_{A} - {[H_{3} O^{+}]}_{é q} \end{cases}$

$K_{A} = \frac{{[H_{3} O^{+}]}_{é q} . {[H_{3} O^{+}]}_{é q}}{C_{A} - {[H_{3} O^{+}]}_{é q}} K_{A} = \frac{{[H_{3} O^{+}]}_{é q}^{2}}{C_{A} - {[H_{3} O^{+}]}_{é q}} K_{A} = \frac{10^{- 2 p H}}{C_{A} - 10^{- p H}}$

ت.ع:

$K_{A} = \frac{10^{- 2 \times 3, 4}}{10^{- 2} - 10^{- 3, 4}} = 1, 65 . 10^{- 5}$

التمرين 2

الموجات: انتشار موجة

تعتبر الموجات الصوتية والموجات فوق الصوتية موجات ميكانيكية قابلة للانتشار في أوساط مختلفة وتوظف في مجالات عدة وتتميز كل منها بمجال للترددات

يهدف هذا التمرين الى تحديد خاصيات انتشار موجة وطبيعة وسط انتشارها

$1$ عرف الموجة الميكانيكية المتوالية

$2$ اختر الاقتراح الصحيح من بين مايلي:

$أ$ الموجات الصوتية وفوق الصوتية موجات مستعرضة
$ب$ تنتشر الموجات الصوتية في الهواء بفعل حركة انضغاط وتمدد طبقات الهواء
$ج$ الموجات فوق الصوتية موجات مسموعة من طرف الانسان
$د$ يتغير تردد الموجات الصوتية وفوق الصوتية بتغير وسط الانتشار

$3$ يبعث مكبر للصوت $S$ صوتا عبر أنبوب يحتوي على غاز

يوجد داخل الانبوب ميكروفونان $M_{1}$ و $M_{2}$ على استقامة واحدة مع $S$ وعلى نفس المسافة $D$ منه

نربط $M_{1}$ و $M_{2}$ براسم التذبذب (الشكل $1$ ). نبقي $M_{1}$ ثابتا ونزيح $M_{2}$ نحو اليمين وفق المحور $S x$ الى أن نحصل على أول توافق في الطور للمنحنيين المحصل عليهما في الرسم التذبذبي (الشكل $2$ )

المسافة الفاصلة بين $M_{1}$ و $M_{2}$ في هذه الحالة هي: $d = 15, 6 c m$

نعطي الحساسية الأفقية لراسم التذبذب: $100 μ s / d i v$

$1 - 3$ بين أن قيمة طول الموجة للموجة الصوتية المنتشرة في الأنبوب هي: $λ = 15, 6 c m$

$2 - 3$ عين مبيانيا قيمة الدور $T$ للموجة الصوتية

$3 - 3$ حدد قيمة $v$ سرعة انتشار الموجة في الغاز

$4 - 3$ يعطي الجدول التالي سرعة انتشار موجة صوتية في بعض الغازات في نفس ظروف إنجاز هذه التجربة:

سرعة الانتشار $v (m . s^{- 1})$

الغاز	ثنائي الأكسيجين	ثنائي الكلور	ثنائي الهيدروجين	ثنائي الازوت
سرعة الانتشار $v (m . s^{- 1})$	$324$	$217$	$1300$	$346$

استنتج الغاز المكون لوسط الانتشار

$5 - 3$ اختر الاقتراح الصحيح من بين مايلي:

تعبير استطالة الموجة المستقبلة من طرف الميكروفون $M_{2}$ بدلالة استطالة المنبع $S$ هو:

$أ$ $y_{M_{2}} (t) = y_{s} (t - \frac{d}{v})$
$ب$ $y_{M_{2}} (t) = y_{s} (t - \frac{D}{v})$
$ج$ $y_{M_{2}} (t) = y_{s} (t - \frac{d + D}{v})$
$د$ $y_{M_{2}} (t) = y_{s} (t - \frac{d - D}{v})$

الموجات: انتشار موجة

$1$ تعريف الموجة الميكانيكية المتوالية:

الموجة الميكانيكية المتوالية هي تتابع مستمر لموجة ميكانيكية ناتجة عن اضطراب مستمر ومصان للمنبع

$2$ الاقتراح الصحيح هو ب

تنتشر الموجات الصوتية في الهواء بفعل حركة انضغاط وتمدد طبقات الهواء

$3$

$1 - 3$ بما أن المنحنيين على توافق في الطور لأول مرة فإن المسافة بين $M_{1}$ و $M_{2}$ تساوي طول الموجة

$λ = d = 15, 6 c m$

$2 - 3$ التعيين المبياني للدور $T$ :

$T = 4, 5 d i v \times 100 μ s . d i v^{- 1} = 450 μ s = 4, 5 . 10^{- 4} S$

$3 - 3$ تحديد قيمة سرعة انتشار الغاز:

$v = \frac{λ}{T} \Rightarrow v = \frac{15, 6 . 10^{- 2}}{4, 5 . 10^{- 4}} \Rightarrow v = 346, 7 m . s^{- 1}$

$4 - 3$ بالاعتماد على نتائج الجدول الغاز الذي سرعة انتشاره تقارب $346 m . s^{- 1}$ هو غاز ثنائي الازوت $N_{2}$

$5 - 3$ استطالة الموجة المستقبلة من طرف الميكروفون $M_{2}$ بدلالة استطالة المنبع $S$ (حيث $S M_{2} = d + D$ ) هو: $ج$

$y_{M_{2}} (t) = y_{s} (t - \frac{d + D}{v})$

3
التمرين 3
الكهرباء: تحديد المقادير المميزة لمكثف ووشيعة

تحتوي مجموعة من الأجهزة الإلكترونية على ثنائيات قطب متنوعة من بينها الموصلات الأومية والوشيعات والمكثفات... وتشكل دراسة الدارات الكهربائية الموجودة في هذه الأجهزة مناسبة لتحليل تصرفها من الناحية الكهربائية والطاقية أو تعرف وظيفتها أو تحديد المقادير المميزة لمكوناتها

يهدف هذا التمرين إلى دراسة استجابة ثنائي القطب $R L$ لرتبة توتر، ودراسة التذبذبات الكهربائية في دارة $R L C$ متوالية

$1$ استجابة ثنائي القطب $R L$ لرتبة توتر

لدراسة استجابة ثنائي القطب $R L$ لرتبة توتر صاعدة ننجز التركيب الممثل في الشكل $(1)$ والمكون من:

مولد كهربائي قوته الكهرمحركة $E = 6 V$ ومقاومته الداخلية مهملة

موصل أومي مقاومته $R = 16 Ω$

وشيعة معامل تحريضها $L$ ومقاومتها $r$

قاطع التيار $K$

نغلق قاطع التيار $K$ عند اللحظة $t = 0$

$1 - 1$ أثبت أن المعادلة التفاضلية التي تحققها $i (t)$ شدة التيار الكهربائي المار في الدارة تكتب كما يلي:

$\frac{d i}{d t} + \frac{R + r}{L} . i = \frac{E}{L}$

$2 - 1$ نعاين على شاشة راسم التذبذب الذاكراتي التوتر $u_{R} (t)$ بين مربطي الموصل الأومي

حدد، معللا جوابك، من بين منحنيي الشكل $(2)$ رقم المنحنى الممثل لتغيرات التوتر $u_{R} (t)$

$3 - 1$ تحقق أن قيمة $I_{0}$ شدة التيار الكهربائي في النظام الدائم هي: $I_{0} = 0, 25 A$

$4 - 1$ قيمة التوتر بين مربطي الوشيعة في النظام الدائم هي: $u_{L} = 2 V$ ، اُحسب قيمة $r$

$5 - 1$ يمثل $(T)$ المماس للمنحنى $u_{R} (t)$ عند $t = 0$ عين مبيانيا قيمة $τ$ ثابتة الزمن، ثم بين أن: $L = 0, 24 H$

$2$ التذبذبات الكهربائية في دارة $R L C$ متوالية

نركب الوشيعة $(L, r)$ السابقة عند اللحظة $t_{0} = 0$ مع مكثف سعته $C$ مشحون بدئيا بالمولد السابق (الشكل $3$ )

يعطي منحنى الشكل $(4)$ تغيرات التوتر $u_{c} (t)$ بين مربطي المكثف

$1 - 2$ اِختر الاقتراح الصحيح من بين ما يلي:

قيمة شبه الدور $T$ للتذبذبات الكهربائية الحرة هي:

$أ$ $T = 2 m s$

$ب$ $T = 4 m s$

$ج$ $T = 20 m s$

$د$ $T = 40 m s$

$2 - 2$ استنتج قيمة $C$ (نعتبر أن شبه الدور $T$ يساوي الدور الخاص $T_{0}$ للمتذبذب $L C$ ونأخذ $π^{2} = 10$ )

$3 - 2$ حدد قيمة $∆ ε$ تغير الطاقة الكلية في الدارة بين اللحظتين $t_{0} = 0$ و $t_{1} = 8 m s$ . فسر هذه النتيجة

$4 - 2$ لصيانة التذبذبات الكهربائية، نركب على التوالي مع المكثف والوشيعة السابقين مولدا يزود الدارة بتوتر $u_{g}$ يتناسب اطرادا مع شدة التيار المار فيها، حيث $u_{g} = k . i$ ( $k$ ثابتة موجبة)

$1 - 4 - 2$ اُذكر دور المولد من منظور طاقي

$2 - 4 - 2$ حدد قيمة $k$

الكهرباء: تحديد المقادير المميزة لمكثف ووشيعة

$1 - 1$ التحقق من المعادلة التفاضلية:

حسب قانون إضافية التوترات: $u_{L} + u_{R} = E$

حسب قانون أوم:

$L . \frac{d i}{d t} + r i + R i = E \Rightarrow \frac{d i}{d t} + \frac{R + r}{L} . i = \frac{E}{L}$

$2 - 1$ التوتر بين مربطي الموصل الأومي يكتب: $u_{R} = R . i$

عند اللحظة $t = 0$ يكون التيار منعدما أي: $u_{R} (0) = 0$ المنحنى يمر من أصل المعلم

المنحنى $(1)$ يمثل تغيرات التوتر $u_{R} = (t)$

$3 - 1$ التحقق من قيمة $I_{0}$ :

في النظام الدائم تستقر قيمة شدة التيار عند القيمة $I_{0}$ ومنه يصبح تعبير التوتر $u_{R}$ هو: $u_{R} (\infty) = R . I_{0}$ أي:

$I_{0} = \frac{u_{R} (\infty)}{R}$

مبيانيا نجد: $u_{R} (\infty) = 4 V$

ت.ع:

$I_{0} = \frac{4}{16} = 0, 25 A$

$4 - 1$ تعبير التوتر بين مربطي الوشيعة في النظام الدائم هو $u_{L} (\infty) = r I_{0}$ أي:

$r = \frac{u_{L} (\infty)}{I_{0}} = \frac{2}{0, 25} = 8 Ω$

$5 - 1$ مبيانيا مماس المنحنى $u_{R} (t)$ عند اللحظة $t = 0$ يقاطع مقارب المنحنى عند نقطة أفصولها $τ = 10 m s$

لدينا: $τ = \frac{L}{R + r}$ أي: $L = (R + r) τ$

ت.ع:

$L = (16 + 8) \times 10 . 10^{- 3} = 0, 24 H$

$2$

$1 - 2$ شبه الدور $T$ للتذبذبات الكهربائية هو: الاقتراح $ب$ $T = 4 m s$

تعليل الجواب ليس مطلوبا

$2 - 2$ استنتاج قيمة $C$ :

لدينا حسب تعبير الدور الخاص: $T_{0} = 2 π \sqrt{L . C}$

بما أن $T_{0} \approx T$ فإن:

$T = 2 π \sqrt{L . C} \Rightarrow T^{2} = 4 π^{2} L . C \Rightarrow C = \frac{T^{2}}{4 π^{2} L}$

ت.ع:

$C = \frac{{(4 . 10^{- 3})}^{2}}{4 \times 10 \times 0, 24} = 1, 67 . 10^{- 6} F = 1, 67 μ F$

$3 - 2$ تحديد قيمة التغير $∆ E$ للطاقة الكلية بين اللحظتين $t_{0} = 0$ و $t_{1} = 8 m s$ :

مبيانيا عند اللحظة $t_{0} = 0$ التوتر بين مربطي المكثف قصوي ويساوي $u_{c} (0) = 6 V$ . وهذا يعني أن شدة التيار في هذه اللحظة منعدمة وبالتالي الطاقة المخزونة في الوشيعة $E_{m}$ منعدمة

إذن الطاقة الكلية للدارة الكهربائية في هذه اللحظة تساوي الطاقة المخزونة في المكثف

$E_{e} (t_{0}) = \frac{1}{2} C . u_{c}^{2} (t_{0}) \Rightarrow ξ = \frac{1}{2} C . u_{c}^{2} (t_{0})$

وعند اللحظة $t_{1} = 8 m s$ لدينا: $u_{c} (t_{1}) = 5 V$ . الطاقة الكلية عند هذه اللحظة مخزونة في المكثف تكتب:

$E_{e} (t_{1}) = \frac{1}{2} C . u_{c}^{2} (t_{1}) \Rightarrow ξ = \frac{1}{2} C . u_{c}^{2} (t_{1})$

تغير الطاقة الكلية سالب لأنها تتناقص وسبب تناقصها هو ظاهرة الخمود وهي ناتجة عن وجود المقاومة

$4 - 2$

$1 - 4 - 2$ يعوض المولد الطاقة المبددة بمفعول جول

$2 - 4 - 2$ تحديد قيمة $r$

حسب قانون إضافية التوترات: $u_{L} + u_{c} = u_{G}$

حسب قانون أوم: $L . \frac{d i}{d t} + r i + u_{c} = k i$

ومنه:

$L . \frac{d i}{d t} + (r - k) i + u_{c} = 0 L C . \frac{d^{2} u_{c}}{d^{2} t} + (r - k) C . \frac{d u_{c}}{d t} + u_{c} = 0$

لكي تكون الدارة مقر تذبذبات جيبية يجب أن تكتب المعادلة التفاضلية على الشكل:

$L C . \frac{d^{2} u_{c}}{d^{2} t} + u_{c} = 0$

أي أن: $r - k = 0$ . ومنه:

$k = r = 8 Ω$
4
التمرين 4
الميكانيك: الحركة المستوية - المتذبذب {جسم صلب - نابض}

تتنوع حركة الأجسام الصلبة بفعل التأثيرات الميكانيكية المطبقة عليها، وتوفر مخططات السرعات والطاقات، المقرونة بحركة هذه الأجسام معطيات تمكن من تحديد طبيعة الحركات وبعض البارامترات المميزة لها

يهدف هذا التمرين إلى دراسة كل من حركة جسم صلب فوق مستوى مائل وحركة متذبذب

$1$ انزلاق جسم صلب فوق مستوى مائل

نطلق بدون سرعة بدئية عند اللحظة $t = 0$ جسما صلبا $(S)$ كتلته $m = 0, 2 k g$ فوق مستوى مائل بالزاوية $a = 30 °$ بالنسبة للمستوى الأفقي (الشكل $1$ )

يخضع الجسم $(S)$ أثناء حركته لاحتكاكات مطبقة من طرف المستوى المائل ننمذجها بقوة $\vec{f}$ ثابتة اتجاهها مواز للمسار ومنحاها معاكس لمنحى الحركة

لدراسة حركة $G$ نختار معلما $(O, \vec{i})$ مرتبطا بالأرض نعتبره غاليليا حيث $x_{G}$ أفصول $G$ عند اللحظة $t = 0$ منعدم

$1 - 1$ بتطبيق القانون الثاني لنيوتن، بين أن تعبير التسارع $a_{G}$ لمركز القصور $G$ للجسم $(S)$ هو:

$a_{G} = g . \sin a - \frac{f}{m}$

$2 - 1$ مكنت الدراسة التجريبية من الحصول على مخطط السرعة $v_{G} (t)$ (الشكل $2$ )

أوجد باستغلال مخطط السرعة قيمة التسارع $a_{G}$

$3 - 1$ استنتج قيمة $f$ . نعطي $g = 10 m . s^{- 2}$

$4 - 1$ اُكتب المعادلة الزمنية $x_{G} (t)$ لحركة $G$

$2$ دراسة حركة متذبذب أفقي

نثبت الجسم $(S)$ السابق بنابض أفقي لفاته غير متصلة وكتلته مهملة وصلابته $K$ ، فنحصل على مجموعة متذبذبة {جسم صلب - نابض}(الشكل $3$ )

عند التوازن ينطبق مركز القصور $G$ للجسم $(S)$ مع الأصل $O$ لمعلم الفضاء $(O, \vec{i})$ المرتبط بالأرض والذي نعتبره غاليليا. نزيح الجسم $(S)$ عن موضع توازنه في المنحى الموجب بالمسافة $X_{m} = 4 c m$ ثم نحرره بدون سرعة بدئية عند اللحظة $t_{0} = 0$ .

نعتبر الاحتكاكات مهملة

$1 - 2$ أعطى قياس المدة الزمنية لعشر $(10)$ تذبذبات حرة القيمة $∆ t = 8, 9 s$

$1 - 1 - 2$ أوجد قيمة $T_{0}$ الدور الخاص للتذبذبات

$2 - 1 - 2$ اُحسب قيمة $K$ ( نأخذ $π^{2} = 10$ )

$3 - 1 - 2$ حدد منحى وشدة قوة الارتداد $\vec{F}$ المطبقة من طرف النابض على الجسم $(S)$ عند اللحظة $t = \frac{T_{0}}{2}$
.
$2 - 2$ يمثل الشكل $(4)$ مخططات الطاقة الحركية $E_{c}$ وطاقة الوضع المرنة $E_{p e}$ والطاقة الميكانيكية $E_{m}$ للمتذبذب المدروس

$1 - 2 - 2$ اقرن، معللا جوابك، كل منحنى بالطاقة الموافقة له

$2 - 2 - 2$ أوجد مبيانيا الأفصولين $x_{1}$ و $x_{2}$ لمركز القصور $G$ اللذين تكون عندهما $E_{c} = 3 E_{p e}$ حيث $(x_{1} > x_{2})$

$3 - 2 - 2$ أوجد قيمة $W (\vec{F})$ شغل قوة الارتداد المطبقة من طرف النابض على الجسم $(S)$ خلال انتقال مركز قصوره من الموضع ذي الأفصول $x_{1}$ إلى الموضع ذي الأفصول $x_{2}$

الميكانيك: الحركة المستوية - المتذبذب {جسم صلب - نابض}

$1$ انزلاق جسم صلب فوق مستوى مائل

$1 - 1$ إثبات تعبير التسارع:

المجموعة المدروسة: الجسم $(S)$

جرد القوى:

$\vec{P}$ : وزن الجسم

$\vec{R}$ : تأثير المستوى المائل

نعتبر المعلم $(O, \vec{i})$ المرتبط بالأرض معلما غاليليا

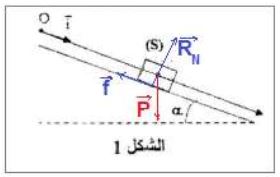
تطبيق القانون الثاني لنيوتن: $\sum {\vec{F}}_{e x t} = m . {\vec{a}}_{G}$

$\vec{P} + \vec{R} = m . {\vec{a}}_{G}$

الإسقاط على المحور $O x$

$P_{x} + R_{x} = m a_{G x} m . g . \sin a - f = m . a_{G} a_{G} = g . \sin a - \frac{f}{m}$

$2 - 1$ قيمة التسارع $a_{G}$

مخطط السرعة $v_{G} (t)$ عبارة عن دالة خطية تكتب: $v_{G} = k t$ حيث $k$ المعامل الموجه

$k = \frac{∆ v_{G}}{∆ t} = \frac{(1, 2 - 0) m . s^{- 1}}{(0, 5 - 0) s} = 2, 4 m . s^{- 2}$

استنتاج التسارع:

$a_{G} = \frac{d v_{G}}{d t} = k = 2, 4 m . s^{- 2}$

$3 - 1$ استنتاج قيمة $f$ :

من المعادلة $m . g . \sin a - f = m . a_{G}$ نحصل على : $f = m . g . \sin a - m . a_{G} \Rightarrow f = m (g . \sin a - a_{G})$

ت.ع:

$f = 0, 2 \times (10 \times \sin 30 ° - 2, 4) = 0, 52 N$

$4 - 1$ المعادلة الزمنية للحركة المستقيمية المنتظمة تكتب:

$x_{G} (t) = \frac{1}{2} a_{G} t^{2} + v_{0} . t + x_{0}$

عند اللحظة $t = 0$ حسب المعطيات $x_{0} = 0$ وباستعمال مبيان الشكل $2$ نجد: $v_{0} = 0$ ومنه:

$x_{G} (t) = \frac{1}{2} \times 2, 4 \times t^{2} = 1, 2 . t^{2}$

$2$ دراسة حركة متذبذب أفقي

$1 - 2$

$1 - 1 - 2$ إيجاد قيمة الدور الخاص $T_{0}$ :

لدينا $∆ t = n . T_{0}$

ومنه:

$T_{0} = \frac{∆ t}{n} = \frac{8, 9}{10} = 0, 89 s$

$2 - 1 - 2$ حساب $K$ صلابة النابض:

لدينا:

$T_{0} = 2 π \sqrt{\frac{m}{k}} \Rightarrow T_{0}^{2} = 4 π^{2} . \frac{m}{k} \Rightarrow K = \frac{4 π^{2} . m}{T_{0}^{2}}$

ت.ع:

$K = \frac{4 \times 10 \times 0, 2}{0, 89^{2}} = 10 N . m^{- 1}$

$3 - 1 - 2$ تحديد منحى وشدة قوة الارتداد $\vec{F}$ عند اللحظة $t = \frac{T_{0}}{2}$ :

لدينا:

$\vec{F} = - K \vec{O G} = - K x \vec{i}$

المعادلة الزمنية للحركة التذبذية تكتب:

$x (t) = X_{m} \cos (\frac{2 π}{T_{0}} . t + φ)$

نحدد $φ$ باستعمال الشروط البدئية:

عند $t_{0} = 0$ لدينا: $x (0) = X_{m}$ ومنه   $\cos φ = 1$ أي: $φ = 0$

المعادلة الزمنية تكتب:

$x (t) = X_{m} \cos (\frac{2 π}{T_{0}} . t)$

عند اللحظة $t = \frac{T_{0}}{2}$ أفصول مركز قصور الجسم $(S)$ يكون:

$x (\frac{T_{0}}{2}) = X_{m} \cos (\frac{2 π}{T_{0}} . \frac{T_{0}}{2}) = X_{m} cosπ = - X_{m}$

$\vec{F} = - K (- X_{m}) \vec{i} = K X_{m} \vec{i}$ إذن منحى القوة   $\vec{F}$ هو منحى $\vec{i}$

وشدتها هي: $F = K . X_{m}$

ت.ع:

$F = 10 \times 4 . 10^{- 2} = 0, 4 N$

$2 - 2$

$1 - 2 - 2$ المنحنى الموافق لكل طاقة:

عند اللحظة $t_{0} = 0$ لدينا $x = X_{m}$ أي أن طاقة الوضع المرنة تكون قصوية وبالتالي المنحنى $1$ يوافق $E_{p e}$ طاقة الوضع المرنة

عند نفس اللحظة سرعة الجسم منعدمة ومنه تكون الطاقة الحركية منعدمة وبالتالي المنحنى $2$ يوافق $E_{c}$ الطاقة الحركية

بما أن $E_{m} = E_{c} + E_{p e}$ فإن المنحنى $3$ يوافق $E_{m}$ الطاقة الميكانيكية

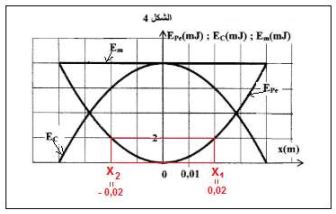
$2 - 2 - 2$ التعيين المبياني لـ   $x_{1}$ و $x_{2}$ :

لنحدد $E_{p e}$ عندما يكون   $E_{c} = 3 E_{p e}$ :

لدينا: $E_{m} = E_{c} + E_{p e} = 3 E_{p e} + E_{p e} = 4 E_{p e}$

أي: $E_{p e} = \frac{E_{m}}{4} = \frac{8}{4} = 2 m J$

باستعمال مبيان الشكل $4$ نجد: $x_{1} = 2 . 10^{- 2} m = 2 c m$    و $x_{2} = - 2 . 10^{- 2} m = - 2 c m$

$3 - 2 - 2$ قيمة شغل قوة الارتداد أثناء الانتقال من الموضع   $x_{1}$ الى الموضع $x_{2}$ :

لدينا:

$W_{1 \to 2} (\vec{F}) = - ∆ E_{p e} = - (E_{p e 2} - E_{p e 1}) = E_{p e 1} - E_{p e 2}$

بما أن حسب المبيان: $E_{p e 1} = E_{p e 2} = 2 m J$ فإن: $W_{1 \to 2} (\vec{F}) = 0$

ملحوظة: يمكن إنجاز التطبيق العددي نحصل على نفس النتيجة حيث:

$W_{1 \to 2} (\vec{F}) = \frac{1}{2} . K . (x_{1}^{2} - x_{2}^{2}) W_{1 \to 2} (\vec{F}) = \frac{1}{2} \times 10 \times [{(2 . 10^{- 2})}^{2} - {(- 2 . 10^{- 2})}^{- 2}] W_{1 \to 2} (\vec{F}) = 0$