الميكانيك
الجزء الأول: دراسة حركة كرة في مجال الثقالة المنتظم
إثبات المعادلتین الزمنیتین
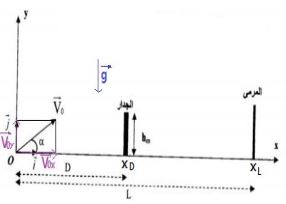
تخضع الكرة لوزنھا فقط
نطبق القانون الثاني لنیوتن في المعلم الذي نعتبره غالیلیا
الشروط البدئیة عند :
الإسقاط على :
الحركة مستقیمیة منتظمة على المحور
المعادلة الزمنیة:
ت.ع :
الاسقاط على
الحركة مستقیمیة متغیرة بانتظام على
المعادلة الزمنیة :
�
ت.ع :
استنتاج معادلة المسار
نعوض في في المعادلة :
ت.ع:
التحقق من أن الكرة تمر فوق الجدار
أفصول الجدار في المعلم ھو
لنبحث عن الأرتوب ونقارنه مع �
نلاحظ أن: وبالتالي الكرة تمر فوق الجدار
تحدید قیمة السرعة
لنحدد تاریخ دخول الكرة الى المرمى ذي الأفصول :
ت.ع:
منظم السرعة یكتب:
و
الجزء الثاني: دراسة طاقیة لحركة نواس بسیط
التحدید المبیاني ل � و �
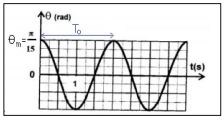
اختیار التعبیر الصحیح ل
لنستعمل معادلة الابعاد للتعبیر
نعلم أن:
ومنه:
وحدة � ھي الثانیة وبالتالي التعبیر الصحیح ھو
حساب طول النواس البسیط
ت.ع:
الطاقة المیكانیكیة � :
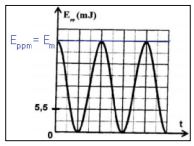
عند اللحظة � لدینا مبیانیا:
القیمة المطلقة للسرعة عند موضع التوازن:
عند موضع التوازن لدینا:
ت.ع:
نستنتج :