الامتحان الوطني الموحد 2014 الدورة العادية: الموضوع والتصحيح

1
التمرين 1
الكيمياء

حمض السليسليك هو حمض كربوكسيلي عطري عديم اللون يستخلص طبيعيا من بعض النباتات كالصفصاف الأبيض وإكليلية المروج ، له عدة فوائد حيث يستعمل في علاج بعض الأمراض الجلدية وكدواء لتخفيف صداع الرأس وكمخفض لدرجة حرارة الجسم كما يعتبر المركب الرئيسي لتصنيع دواء الأسبرين

من خلال مجموعتيه المميزتين، يمكن لحمض السليسليك أن يلعب دور الحمض أو دور الكحول وذلك حسب ظروف تجريبية معينة

يهدف التمرين الى دراسة تفاعل حمض السليسليك مع الماء والى معايرته بواسطة محلول قاعدي ثم الى تفاعله مع حمض الإيثانويك

نرمز لحمض السليسليك بـ $A H$ ولقاعدته المرافقة بـ $A^{-}$

معطيات:

تمت جميع القياسات عند درجة الحرارة $25 ° C$

صيغة حمض السليسليك:

الموصليات المولية الأيونية: $λ_{A^{-}} = 3, 62 . 10^{- 3} S . m^{2} . m o l^{- 1}$ و $λ_{H_{3} O^{+}} = 35 . 10^{- 3} S . m^{2} . m o l^{- 1}$

نهمل تأثير الأيونات $H O^{-}$ على موصلية المحلول ، ونكتب تعبير الموصلية $σ$ لمحلول مائي مخفف للحمض $A H$ كالتالي: $σ = λ_{A^{-}} . [A^{-}] + λ_{H_{3} O^{+}} . [H_{3} O^{+}]$

بالنسبة للمزدوجة $p K_{A} = 3 : A H_{(a q)} / A_{(a q)}^{-}$

جدول مناطق انعطاف بعض الكواشف الملونة:

$1$ دراسة تفاعل حمض السليسليك مع الماء

نعتبر محلولا مائيا $(S)$ لحمض السليسليك تركيزه المولي $C = 5 . 10^{- 3} m o l . L^{- 1}$ وحجمه $V = 100 m L$ أعطى قياس موصلية المحلول $(S)$ القيمة $σ = 7, 18 . 10^{- 2} S . m^{- 1}$

$1 - 1$ انقل الجدول الوصفي التالي على ورقة التحرير وأتممه

$2 - 1$ أوجد تعبير $x_{é q}$ تقدم التفاعل عند التوازن بدلالة $λ_{λ}$ و $λ_{H_{3} O^{+}}$ و $σ$ و $V$ ثم احسب قيمة $x_{é q}$

$3 - 1$ بين أن القيمة التقريبية لـ $p H$ المحلول $(S)$ هي $2, 73$

$4 - 1$ احسب خارج التفاعل عند التوازن $Q_{r . é q}$

$2$ معايرة حمض السليسليك بواسطة محلول هيدروكسيد الصوديوم

نعاير بتتبع قياس $p H$ الحجم $V_{A} = 15 m L$ من محلول مائي لحمض السليسليك $A H$ تركيزه $C'_{A}$ بواسطة محلول مائي $(S_{B})$ لهيدروكسيد الصوديوم $N a_{(a q)}^{+} + H O_{(a q)}^{-}$ ذي التركيز $C_{B} = 0, 2 m o l . L^{- 1}$

$1 - 2$ ارسم تبيانة التركيب التجريبي لإنجاز هذه المعايرة معينا أسماء المعدات والمحاليل

$2 - 2$ اكتب المعادلة الكيميائية المنمذجة للتحول الحاصل أثناء هذه المعايرة

$3 - 2$ يمثل المنحنى التالي تغير $p H$ الخليط بدلالة الحجم $V_{B}$ للمحلول $(S_{B})$ لهيدروكسيد الصوديوم المضاف

$1 - 3 - 2$ حدد الإحداثيتين $V_{B E}$ و $p H_{E}$ لنقطة التكافؤ

$2 - 3 - 2$ احسب التركيز $C'_{A}$

$3 - 3 - 2$ بالرجوع الى الجدول الوارد ضمن المعطيات, عين الكاشف الملون الملائم لإنجاز هذه المعايرة في غياب جهاز $p H$ متر, علل جوابك

$4 - 3 - 2$ حدد الخارج $\frac{{[A^{-}]}_{e q}}{{[A H]}_{e q}}$ عند إضافة الحجم $V_{B} = 6 m L$ من المحلول $(S_{B})$ للخليط التفاعلي

$3$ دراسة تفاعل حمض السليسليك مع حمض الإيثانويك

لإنجاز تفاعل الأسترة بين حمض الإيثانيوك $C H_{3} C O O H$ وحمض السليسليك الذي يلعب دور الكحول في هذا التحول الكيميائي نسخن بالارتداد خليطا حجمه $V$ ثابت يتكون من كمية المادة $n_{1} = 0, 5 m o l$ لحمض الإيثانويك ومن كمية المادة $n_{2} = 0, 5 m o l$ لحمض السليسليك بعد إضافة قطرات من حمض الكبريتيك المركز كحفاز

$1 - 3$ باستعمال الصيغ الكيميائية، اكتب المعادلة الكيميائية المنمذجة لهذا التفاعل

$2 - 3$ نحصل عند التوازن على كمية مادة الإستر المتكون $n_{e q} (e s t e r) = 3, 85 . 10^{- 2} m o l$ . احسب المردود $r$ لتفاعل الأسترة

$3 - 3$ اذكر طريقتين للرفع من مردود هذا التفاعل بالحفاظ على نفس المتفاعلات

الكيمياء

$1$ دراسة تفاعل حمض الساليسيليك مع الماء

$1 - 1$ ملأ الجدول الوصفي

$2 - 1$ تعبير $X_{é q}$

حسب تعريف الموصلية:

$σ = λ_{(A^{-})} {[A^{-}]}_{é q} + λ_{H_{3} O^{+}} {[H_{3} O^{+}]}_{é q}$

حسب الجدول الوصفي:

${[A^{-}]}_{_{é q}} = {[H_{3} O^{+}]}_{_{é q}} = \frac{x_{_{é q}}}{V} \Rightarrow σ = λ_{(A^{-})} \frac{x_{_{é q}}}{V} + λ_{(H_{3} O^{+})} \frac{x_{_{é q}}}{V} \Rightarrow σ = (λ_{(A^{-})} + λ_{(H_{3} O^{+})}) \frac{x_{_{é q}}}{V} \Rightarrow x_{_{é q}} = \frac{σ . V}{λ_{(A^{-})} + λ_{(H_{3} O^{+})}}$

ت.ع:

$x_{é q} = \frac{7, 18 . 10^{- 2} S . m^{- 1} \times 100 . 10^{- 6} m^{3}}{(35 . 10^{- 3} + 3, 62 . 10^{3}) S . m^{2} . m o l^{- 1}} = 1, 86 . 10^{- 4} m o l$

$3 - 1$ إثبات أن: $p H ≃ 2, 73$

$\{\begin{cases} {[H_{3} O^{+}]}_{é q} = \frac{x_{é q}}{V} \\ p H = - \log [H_{3} O^{+}] \end{cases} \Rightarrow p H = - \log (\frac{x_{é q}}{V})$

ت.ع:

$p H = - \log (\frac{1, 86 . 10^{- 4}}{100 . 10^{- 3}}) ≃ 2, 73$

$4 - 1$ خارج التفاعل عند التوازن: $Q_{r, é q} = \frac{{[A^{-}]}_{é q} {[H_{3} O^{+}]}_{é q}}{{[A H]}_{é q}}$

حسب الجدول الوصفي:

$\{\begin{cases} {[A^{-}]}_{é q} = {[H_{3} O^{+}]}_{é q} \\ {[A H]}_{é q =} \frac{C . V - x_{é q}}{V} = C - \frac{x_{é q}}{V} \end{cases} \Rightarrow \{\begin{cases} {[A^{-}]}_{é q} = {[H_{3} O^{+}]}_{é q} \\ {[A H]}_{é q =} C - {[H_{3} O^{+}]}_{é q} \end{cases} \Rightarrow \{\begin{cases} {[A^{-}]}_{é q} = {[H_{3} O^{+}]}_{é q} = 10^{- p H} \\ {[A H]}_{é q =} C - 10^{- p H} \end{cases} \Rightarrow Q_{r . é q} = \frac{{({[H_{3} O^{+}]}_{é q})}^{2}}{C - {[H_{3} O^{+}]}_{é q}} = \frac{10^{- 2 p H}}{C - 10^{- p H}}$

ت.ع:

$Q_{r . é q} = \frac{10^{- 2 \times 2, 73}}{5 . 10^{- 3} - 10^{- 2, 73}} = 1, 1 . 10^{- 3}$

$2$ معايرة حمض الساليسليك بواسطة محلول هيدروكسيد الصوديوم

$1 - 2$ تبيانة التركيب التجريبي

$2 - 2$ معادلة التفاعل:

$A H_{(l)} + H O_{(a q)}^{-} \to A_{(a q)}^{-} + H_{2} O_{(l)}$

$1 - 3 - 2$ نستعمل طريقة المماسات لتحديد إحداثيات نقطة التكافؤ

نجد: $p H_{E} = 8$ و $V_{B E} = 15 m L$

$2 - 3 - 2$ حساب التركيز $C'_{A}$ :

حسب علاقة التكافؤ

$C'_{A} . V_{A} = C_{B} . V_{B E} \Rightarrow C'_{A} = \frac{C_{B} . V_{B E}}{V_{A}}$

ت.ع:

$C'_{A} = \frac{0, 2 \times 15}{15} = 0, 2 m o l . L^{- 1}$

$3 - 3 - 2$ الكاشف الملون المناسب لهذه المعايرة هو أحمر الكريزول

لأن $p H_{E}$ تنتمي الى نقطة انعطافه $p H_{E} \in [7, 2 - 8, 8]$

$4 - 3 - 2$ تحديد الخارج $\frac{{[A^{-}]}_{é q}}{{[A H]}_{é q}}$ عند $V_{B} = 6 m L$

بالاعتماد على المنحنى $p H = f (V_{B})$

عند الحجم $V_{B} = 6 m L$ نجد: $p H = 2, 8$

$p H = p K_{A} + \log \frac{{[A^{-}]}_{é q}}{{[A H]}_{é q}} \Rightarrow p H - p K_{A} = \log \frac{{[A^{-}]}_{é q}}{{[A H]}_{é q}} \Rightarrow \frac{{[A^{-}]}_{é q}}{{[A H]}_{é q}} = 10^{p H - p K_{A}} = 10^{2, 8 - 3} \Rightarrow \frac{{[A^{-}]}_{é q}}{{[A H]}_{é q}} = 0, 63$

$3$ دراسة تفاعل حمض الساليسليك مع حمض الإيثانويك

$1 - 3$ معادلة التفاعل

$2 - 3$ مردود التفاعل:

$r = \frac{n_{e x p}}{n_{t h}} = \frac{x_{é q}}{x_{m a x}}$

الجدول الوصفي:

لدينا: $n_{1} = n_{2} = x_{m a x} = 0, 5 m o l$

و $n_{é q} (e s t e r) = x_{é q} = 3, 85 . 10^{- 2} m o l$

$r = \frac{3, 85 . 10^{- 2}}{0, 5} = 0, 077 = 7, 7 %$

$3 - 3$ للزيادة من مردود التفاعل مع الحفاظ على نفس المتفاعلات يمكن:

استعمال أحد المتفاعلين بوفرة

إزالة أحد النواتج الماء، أو الإستر من الوسط التفاعلي
2
التمرين 2
الموجات

غالبا ما تحدث الزلازل التي تقع في أعماق المحيطات ظاهرة طبيعية تدعى تسونامي ، وهي عبارة عن موجات تنتشر على سطح المحيط لتصل الى الشواطئ بطاقة عالية ومدمرة

ننمذج ظاهرة تسونامي بموجات ميكانيكية متوالية دورية تنتشر على سطح الماء بسرعة $v$ تتغير مع عمق المحيط $h$ وفق العلاقة $v = \sqrt{g . h}$ في حالة المياه القليلة العمق مقارنة مع طول الموجة $(λ ≫ h)$ ، حيث الرمز $λ$ يمثل طول الموجة و $g$ شدة الثقالة

نعطي: $g = 10 m . s^{- 2}$

ندرس انتشار موجة تسونامي في جزء من المحيط نعتبر عمقه ثابتا $h = 6000 m$

$1$ علل أن الموجات التي تنتشر على سطح المحيط مستعرضة

$2$ احسب السرعة $v$ للموجات الميكانيكية المنتشرة على سطح الماء في هذا الجزء من المحيط

$3$ علما أن المدة الزمنية الفاصلة بين ذروتين متتاليتين هي $T = 15 m i n$ ، أوجد طول الموجة $λ$

$4$ في الحالة $(λ ≫ h)$ يبقى تردد موجات تسونامي ثابتا خلال انتشارها نحو الشاطئ . كيف يتغير طول الموجة $λ$ عند الاقتراب من الشاطئ؟ علل جوابك

$5$ تمر موجة تسونامي بين جزيرتين $A$ و $B$ يفصل بينهما مضيق عرضه $d = 100 k m$

نفترض أن عمق المحيط بجوار الجزيرتين يبقى ثابتا وأن موجة تسونامي الواردة مستقيمية طول موجتها $λ = 120 k m$ (الشكل)

$1 - 5$ هل تحقق شرط حدوث ظاهرة حيود موجة تسونامي عند اجتيازها المضيق؟ علل الجواب

$2 - 5$ في حالة حدوث الحيود:

أعط معللا جوابك، طول الموجة المحيدة

احسب زاوية الحيود $θ$

الموجات

$1$ الموجة التي تنتشر على سطح الماء مستعرضة لأن اتجاه الانتشار عمودي على اتجاه تشويهها

$2$ حساب سرعة الانتشار:

لدينا: $V = \sqrt{g . h}$

ت.ع:

$V = \sqrt{10 m . s^{- 2} \times 6000 m} ≃ 245 m . s^{- 1}$

$3$ طول الموجة $λ$ :

لدينا: $V = \frac{λ}{T} \Rightarrow λ = V . T$

ت.ع:

$λ = 245 \times 18 \times 60 = 264, 6 k m$

$4$ نعلم أن عندما يكون $λ ≫ h$ فإن التردد $v$ يبقى ثابتا

كما أن: $λ = \frac{V}{v} = \frac{\sqrt{g . h}}{v}$

عند الاقتراب من الشاطئ لدينا $h$ تتناقص و $g = C t e$ و $v = C t e$

ومنه فإن طول الموجة $λ$ يتناقص

$5$

$1 - 5$ لتتحقق ظاهرة الحيود يجب أن يكون $d$ أصغر بقليل أو تقارب طول الموجة $λ$

$λ = 120 k m$ و $d = 100 k m$ ومنه $d < λ$ عرض الشق أصغر بقليل من طول الموجة إذن ظاهرة الحيود تتحقق

$2 - 5$ للموجة المحيدة نفس طول الموجة الواردة $λ = 120 k m$

زاوية الحيود تعطى بالعلاقة: $θ = \frac{λ}{d}$

لدينا: $λ = \frac{\sqrt{g . h}}{v}$

بماأن: $h = C t e$ و $v = C t e$ فإن: $λ = C t e = 120 k m$

ومنه:

$θ = \frac{120}{100} = 1, 2 r a d$
3
التمرين 3
الكهرباء

توجد بالمختبر مواد كيميائية تتأثر برطوبة الهواء. ولتحديد نسبة الرطوبة $x$ داخل مختبر ، اختار تقني القيام بتجربتين وذلك قصد:

التحقق من قيمة معامل التحريض $L$ لوشيعة $(b)$ مقاومتها $r$

تحديد نسبة الرطوبة $x$ بواسطة مكثف تتغير سعته $C$ مع نسبة الرطوبة

$1$ التجربة الأولى: التحقق من قيمة معامل التحريض للوشيعة

ركب تقني المختبر على التوالي العناصر التالية:

موصلا أوميا مقاومته $R = 200 Ω$

الوشيعة $(b)$

مولدا مؤمثلا للتوتر قوته الكهرمحركة $E$

قاطعا للتيار $K$

في هذه التجربة، نعتبر المقاومة الكهربائية $r$ للوشيعة مهملة أمام $R$

عند لحظة $t = 0$ أغلق التقني قاطع التيار وباستعمال وسيط معلوماتي ، عاين التوتر $u_{R} (t)$ بين مربطي الموصل الاومي

بعد المعالجة المعلوماتية للمعطيات حصل على منحنى الشكل $1$ الذي يمثل شدة التيار الكهربائي $i (t)$ المار في الدارة

$1 - 1$ ارسم تبيانة التركيب التجريبي مبينا عليها كيفية ربط الوسيط المعلوماتي لمعاينة $u_{R} (t)$ (يربط الوسيط المعلوماتي بنفس الطريقة التي يربط بها راسم التذبذب)

$2 - 1$ أثبت المعادلة التفاضلية التي تحققها شدة التيار $i (t)$

$3 - 1$ حل هذه المعادلة التفاضلية هو $i (t) = \frac{E}{R} (1 - e^{- \frac{t}{τ}})$

أوجد تعبير $τ$ بدلالة برامترات الدارة

$4 - 1$ تحقق أن معامل التحريض للوشيعة $(b)$ هو $L = 0, 4 H$

$2$ التجربة الثانية: تحديد نسبة الرطوبة باستعمال متذبذب كهربائي

أنجز التقني التركيب التجريبي الممثل في الشكل $2$ والمكون من:

الوشيعة السابقة $(b)$ ذات المقاومة $r$ ومعامل التحريض $L$

المكثف ذي السعة $C$

المولد المؤمثل للتوتر ذي القوة الكهرمحركة $E$

موصل أومي مقاومته $R'$

قاطع التيار $K$ ذي موضعين

مولد كهربائي $G$ يزود الدارة بتوتر $u_{G} = k . i (t)$ حيث $k$ برامتر موجب قابل للضبط

بعد شحن المكثف كليا أرجح التقني قاطع التيار الى الموضع $2$ عند لحظة $t_{0} = 0$ (الشكل $2$ )

يمثل منحنى الشكل $3$ التوتر $u_{c} (t)$ المحصل عليه بين مربطي المكثف في حالة ضيط البرامتر $k$ على القيمة $k = r$

$1 - 2$ أي نظام من أنظمة التذبذب يبرزه هذا المنحنى؟

$2 - 2$ أثبت المعادلة التفاضلية التي يحققها التوتر $u_{c} (t)$

$3 - 2$ يكتب حل هذه المعادلة التفاضلية على الشكل: $u_{c} (t) = U_{0} . \cos (\frac{2 π}{T_{0}} . t)$

أوجد تعبير الدور الخاص $T_{0}$ للمتذبذب للمتذبذب الكهربائي

$4 - 2$ تتغير السعة $C$ للمكثف مع نسبة الرطوبة $x$ حسب العلاقة: $C = 0, 5 . x - 20$ حيث $C$ بالوحدة $(μ F)$ و $x$ نسبة مئوية $(%)$

حدد نسبة الرطوبة $x$ داخل المختبر

الكهرباء

$1$ التجربة الأولى: التحقق من قيمة معامل التحريض للوشيعة

$1 - 1$ تبيانة التركيب التجريبي:

$2 - 1$ إثبات المعادلة التفاضلية التي تحققها شدة التيار:

حسب قانون إضافية التوترات: $E = u_{L} + u_{R}$

حسب قانون أوم: $u_{L} = L \frac{d i}{d t}$ و $u_{R} = R i$

$L \frac{d i}{d t} + R i = E \Rightarrow \frac{L}{R} . \frac{d i}{d t} + i = \frac{E}{R}$

$3 - 1$ إيجاد تعبير $τ$ :

حل المعادلة التفاضلية:

$i (t) = \frac{E}{R} (1 - e^{- \frac{t}{τ}}) \Rightarrow \frac{d i}{d t} = \frac{E}{R} . \frac{1}{τ} e^{- \frac{t}{τ}}$

نعوض في المعادلة التفاضلية:

$\frac{L}{R} . \frac{E}{R . τ} e^{- \frac{t}{τ}} + \frac{E}{R} - \frac{E}{R} e^{- \frac{t}{τ}} = \frac{E}{R} \Rightarrow \frac{E}{R} (\frac{L}{R . τ} - 1) e^{- \frac{t}{τ}} = 0 \Rightarrow \frac{L}{R . τ} - 1 = 0 \Rightarrow τ = \frac{E}{R}$

$4 - 1$ التحقق من $L = 0, 4 H$

مبيانيا نجد: $τ = 2 m s$

لدينا: $τ = \frac{L}{R}$ أي: $L = τ . R$

ت.ع:

$L = 2 . 10^{- 3} \times 200 = 0, 4 H$

$2$ التجربة الثانية: تحديد نسبة الرطوبة باستعمال متذبذب كهربائي

$1 - 2$ النظام الذي يبرزه المنحنى هو النظام الدوري

$2 - 2$ إثبات المعادلة التفاضلية التي يحققها التوتر $u_{C}$ :

حسب قانون إضافية التوترات:

$u_{b} + u_{C} = u_{G} \Rightarrow L \frac{d i}{d t} + r i + u_{C} = r i \Rightarrow L \frac{d i}{d t} + u_{C} = 0$

لدينا:

$i = \frac{d q}{d t} = C \frac{d u_{C}}{d t} \Rightarrow \frac{d i}{d t} = \frac{d}{d t} (C \frac{d u_{C}}{d t}) = C \frac{d^{2} u c}{d t^{2}}$

إذن:

$L C \frac{d^{2} u_{C}}{d t^{2}} + u_{C} = 0 \Rightarrow \frac{d^{2} u_{C}}{d t^{2}} + \frac{1}{L . C} u_{C} = 0$

$3 - 2$ تعبير الدور الخاص $T_{0}$

$u_{C} = U_{0} \cos (\frac{2 π}{T_{0}} t) \Rightarrow \frac{d u_{C}}{d t} = - \frac{2 π}{T_{0}} . U_{0} \sin (\frac{2 π}{T_{0}} t) \Rightarrow \frac{d^{2} u_{C}}{d^{2} t} = - {(\frac{2 π}{T_{0}})}^{2} U_{0} \cos (\frac{2 π}{T_{0}} t) \Rightarrow - {(\frac{2 π}{T_{0}})}^{2} U_{0} \cos (\frac{2 π}{T_{0}} t) + \frac{1}{L . C} U_{0} \cos (\frac{2 π}{T_{0}} t) = 0 \Rightarrow {(\frac{2 π}{T_{0}})}^{2} = \frac{1}{L . C} \Rightarrow \frac{2 π}{T_{0}} = \frac{1}{\sqrt{L . C}} \Rightarrow T_{0} = 2 π \sqrt{L . C}$

$4 - 2$ تحديد $x$ نسبة الرطوبة

$C = 0, 5 x - 20 (μ F) \Rightarrow x = \frac{C + 20}{0, 5} = 2 C + 40$

مبيانيا من الشكل $3$ قيمة الدور الخاص هي: $T_{0} = 5 m s = 5 . 10^{- 3} s$

$T_{0} = 2 π \sqrt{L . C} \Rightarrow T_{0}^{2} = 4 π^{2} L . C \Rightarrow C = \frac{T_{0}^{2}}{4 π^{2} L} C = \frac{{(5 . 10^{- 3})}^{2}}{4 π^{2} \times 0, 4} C = 1, 58 . 10^{- 6} F C ≃ 1, 6 μF$

استنتاج نسبة الرطوبة:

$x = 2 C + 40 = 2 \times 1, 6 + 40 = 43, 2 %$
4
التمرين 4
الميكانيك

(الجزء الأول والثاني مستقلان)

الجزء الأول: دراسة حركة حمولة

تستعمل الرافعات في أوراش البناء، لنقل الحمولات الثقيلة بواسطة أحبال فولاذية مرتبطة بأجهزة خاصة

يهدف هذا التمرين الى دراسة الحركة الرأسية لحمولة، ثم دراسة حركة السقوط الرأسي لجزء منها في الهواء

نأخذ شدة الثقالة: $g = 9, 8 m . s^{- 2}$

$1$ حركة رفع الحمولة

بأحد أوراش البناء، تم تصوير حركة حمولة $(C)$ ، مركز قصورها $G$ وكتلتها $m = 400 k g$ أثناء رفعها

خلال الحركة يطبق الحبل الفولاذي على $(C)$ قوة ثابتة متجهتها $\vec{T}$ (نهمل جميع الاحتكاكات)

ندرس حركة $G$ في معلم $(O, \vec{k})$ مرتبط بالأرض الذي نعتبره غاليليا (الشكل $1$ )

بعد معالجة شريط حركة $(C)$ بواسطة برنم مناسب نحصل على المنحنى الممثل في الشكل $2$ الذي يمثل السرعة $V_{G} (t)$

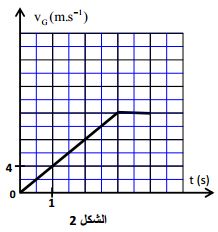
$1 - 1$ حدد طبيعة حركة مركز القصور $G$ في كل من المجالين الزمنيين: $[0; 3 s]$ و $[3 s; 4 s]$

$2 - 1$ بتطبيق القانون الثاني لنيوتن أوجد شدة القوة $\vec{T}$ التي يطبقها الحبل الفولاذي في كل من المجالين الزمنيين: $[0; 3 s]$ و $[3 s; 4 s]$

$2$ السقوط الرأسي لجزء من الحمولة في الهواء

تتوقف الحمولة عن الحركة عند ارتفاع معین.

في لحظة $t = 0$ یسقط منھا جزء $(S)$ كتلته $m_{s} = 30 k g$ ، بدون سرعة بدئیة

ندرس حركة مركز القصور $G_{s}$ للجزء $(S)$ في المعلم $(O, \vec{j})$ بحیث المحور $\vec{O y}$ موجه نحو الأسفل.(الشكل $3$ )

ینطبق موضع $G_{s}$ مع أصل المحور $\vec{O y}$ عند أصل التواریخ

ننمذج تأثیر الھواء على الجزء $(S)$ أثناء حركته بالقوة : $\vec{f} = - k . v^{2} . \vec{j}$ حیث $\vec{v}$ متجھة سرعة $G_{s}$ عند لحظة $t$ و $k = 2, 7$ في النظام العالمي للوحدات

نھمل تأثیر دافعة أرخمیدس أمام القوى الأخرى المطبقة على $(S)$

$1 - 2$ اعتمادا على معادلة الأبعاد ، حدد وحدة الثابتة $k$ في النظام العالمي للوحدات

$2 - 2$ أثبت أن المعادلة التفاضلیة التي تحققھا السرعة $v$ تكتب كما یلي: $\frac{d v}{d t} + 9 . 10^{- 2} . v^{2} = 9, 8$

$3 - 2$ حدد السرعة الحدية $V_{l i m}$ للحركة

$4 - 2$ علما أن سرعة مركز القصور $G_{s}$ عند لحظة $t_{1}$ هي $v_{1} = 2, 75 m . s^{- 1}$ أوجد باعتماد طريقة أولير سرعته $v_{2}$ عند اللحظة $t_{2} = t_{1} + ∆ t$ حيث خطوة الحساب هي $∆ t = 2, 4 . 10^{- 2} s$

الجزء الثاني: الدراسة الطاقية لمجموعة متذبذبة (جسم صلب – نابض)

توجد النوابض في مجموعة من الأجهزة الميكانيكية المختلفة كالسيارات والدراجات...وينتج عنها تذبذبات ميكانيكية

يهدف هذا الجزء الى الدراسة الطاقية لمجموعة ميكانيكية متذبذبة (جسم صلب – نابض) في وضع أفقي

نعتبر متذبذبا ميكانيكيا أفقيا يتكون من جسم صلب $(S)$ كتلته $m$ ومركز قصوره $G$ مثبت بطرف نابض لفاته غير متصلة وكتلته مهملة وصلابته $K = 10 N . m^{- 1}$ الطرف الاخر للنابض مرتبط بحامل ثابت

ينزلق الجسم $(S)$ بدون احتكاك فوق المستوى الأفقي

ندرس حركة المتذبذب في معلم غاليلي $(O, \vec{i})$ مرتبط بالأرض وأصله منطبق مع موضع $G$ عند توازن $(S)$ . نمعلم موضع $G$ عند لحظة $t$ بالأفصول $x$ (الشكل $4$ )

نزيح الجسم $(S)$ أفقيا عن موضع توازنه في المنحى الموجب بالمسافة $X_{0}$ ونحرره بدون سرعة بدئية عند لحظة نعتبرها أصلا للتواريخ

نختار المستوى الأفقي المار من $G$ مرجعا لطاقة الوضع الثقالية، والحالة التي يكون فيها النابض غير مشوه مرجعا لطاقة الوضع المرنة

نحصل بواسطة عدة معلوماتية ملائمة على المنحنيين الممثلين لتغيرات كل من الطاقة الحركية $E_{c}$ وطاقة الوضع المرنة $E_{p e}$ للمجموعة المتذبذبة بدلالة الزمن (الشكل $5$ )

$1$ عين من بين المنحنيين (أ) و (ب) المنحنى الذي يمثل تغيرات الطاقة الحركية $E_{c}$ . علل الجواب

$2$ حدد قيمة الطاقة الميكانيكية $E_{m}$ للمجموعة المتذبذبة

$3$ استنتج قيمة المسافة $X_{0}$

$4$ باعتماد تغير طاقة الوضع المرنة للمجموعة المتذبذبة، أوجد الشغل $W_{A \to O} (\vec{T})$ لقوة الارتداد $\vec{T}$ المطبقة من طرف النابض على $(S)$ عند انتقال $G$ من موضع $A$ أفصوله $x_{A} = X_{0}$ الى الموضع $O$

الميكانيك

الجزء الأول: دراسة حركة حمولة

$1$ حركة رفع الحمولة

$1 - 1$ لتحديد طبيعة حركة $G$ نستعمل الشكل ( $2$ )

في المجال الزمني: $[0; 3 s]$ السرعة عبارة عن دالة خطية إذن حركة $G$ مستقيمية متغيرة بانتظام

في المجال الزمني: $[3 s; 4 s]$ السرعة ثابتة $v_{G} = C t e$ إذن حركة $G$ مستقيمية منتظمة

$2 - 1$ شدة القوة $\vec{T}$

المجموعة المدروسة: {الحمولة}

جرد القوى:

$\vec{P}$ وزن الحمولة

$\vec{T}$ توتر الحبل الفولاذي

باعتبار المعلم $(O, \vec{k})$ المرتبط بالأرض غاليليا نطبق القانون الثاني لنيوتن:

$\sum {\vec{F}}_{e x t} = m . {\vec{a}}_{G} \Rightarrow \vec{T} + \vec{P} = m {\vec{a}}_{G}$

الاسقاط على $O z$ :

$- P + T = m a_{G} \Rightarrow T = m g + m a_{G} = m (g + a_{G})$

خلال المرحلة الأولى لدينا:

$a_{G} = \frac{∆ v_{G}}{∆ t} = \frac{4 - 0}{1 - 0} = 4 m . s^{- 2}$

$T = 400 (9, 8 + 4) = 5520 N$

خلال المرحلة الثانية لدينا: $V_{G} = C t e$ وبالتالي: $a_{G} = 0$

$T = m . g = 400 \times 9, 8 = 3920 N$

$2$ السقوط الرأسي لجزء من الحمولة في الهواء

$1 - 2$ وحدة الثابتة $K$ :

$f = k . v^{2} \Rightarrow k = \frac{f}{V^{2}}$

باستعمال معادلة الابعاد: $[k] = \frac{[f]}{{[V]}^{2}}$

$\{\begin{cases} [f] = \frac{[M] [L]}{{[t]}^{2}} \\ [V] = \frac{[L]}{[t]} \end{cases} \Rightarrow [k] = \frac{\frac{[M] [L]}{{[t]}^{2}}}{\frac{{[L]}^{2}}{{[t]}^{2}}} = \frac{[M] [L] {[t]}^{2}}{{[L]}^{2} {[t]}^{2}} = [M] {[L]}^{- 1}$

وحدة $K$ هي: $k g . m^{- 1}$

$2 - 2$ المعادلة التفاضلية:

يخضع الجزء $S$ خلال سقوطه في الهواء الى القوى التالية:

$\vec{P'}$ وزن الجزء $S$ من الحمولة

$\vec{f}$ القوة المقرونة بتأثير الهواء

تطبيق القانون الثاني لنيوتن : $\vec{P'} + \vec{f} = m_{s} . {\vec{a}}_{G}$

$m_{s} . \vec{g} - K v^{2} \vec{J} = m_{s} . {\vec{a}}_{G}$

الاسقاط على المحور $O z$ :

$m_{s} . g - K v^{2} = m_{s} . a$

$m_{s} . g - K v^{2} = m_{s} . a \Rightarrow \frac{d v}{d t} = g - \frac{K}{m_{s}} v^{2}$

$\frac{d v}{d t} = 9, 8 - \frac{2, 7}{30} v^{2} \Rightarrow \frac{d v}{d t} + 9 . 10^{- 2} v^{2} = 9, 8$

$3 - 2$ تحديد السرعة الحدية $v_{l}$ :

في النظام الدائم يكون: $v = v_{l} = C t e$ أي: $\frac{d v}{d t} = 0$

المعادلة التفاضلية تصبح:

$9 . 10^{- 2} v_{l}^{2} = 9, 8 \Rightarrow v_{l}^{2} = \frac{9, 8}{9 . 10^{- 2}} \Rightarrow v_{l} = \sqrt{\frac{9, 8}{9 . 10^{- 2}}} = 10, 4 m . s^{- 1}$

$4 - 2$ إيجاد السرعة $v_{2}$ :

لدينا:

$\{\begin{cases} a_{1} = 9, 8 - 9 . 10^{- 2} v_{1}^{2} \\ v_{2} = a_{1} . ∆ t + v_{1} \end{cases}$

أي:

$\{\begin{cases} a_{1} = 9, 8 - 9 . 10^{- 2} {(2, 75)}^{2} = 9, 12 m . s^{- 2} \\ v_{2} = 9, 12 \times 2, 4 . 10^{- 2} + 2, 75 = 2, 97 m . s^{- 1} \end{cases} \Rightarrow v_{2} = 2, 97 m . s^{- 1}$

الجزء الثاني: الدراسة الطاقية لمجموعة متذبذبة (جسم صلب – نابض)

$1$ المنحنى الذي يمثل تغيرات الطاقة الحركية هو المنحنى (أ)

تعليل: حسب الشروط البدئية عند $t = 0$ تم تحرير الجسم بدون سرعة بدئية $(v = 0)$ أي $E_{C} = 0$

$2$ تحديد قيمة الطاقة الميكانيكية $E_{m}$

لدينا: $E_{m} = E_{C} + E_{p e} + E_{p p}$

$E_{p p} = 0$ لأن المستوى الأفقي المار من $G$ حالة مرجعية ل $E_{p p}$

عند $t = 0$ لدينا $E_{C} = 0$

ومنه:

$E_{m} = E_{p e m a x} = 2 m J$

$3$ استنتاج المسافة $X_{0}$

$E_{m} = \frac{1}{2} k X_{0}^{2} \Rightarrow X_{0} = \sqrt{\frac{2 . E_{m}}{k}}$

$X_{0} = \sqrt{\frac{2 \times 2 . 10^{- 3}}{10}} = 2 . 10^{- 2} m$

$4$ إيجاد شغل القوة $\vec{F}$ :

$W_{A \to O} (\vec{F}) = - ∆ E_{p e} = - (E_{p e} (o) - E_{p e} (A))$

ت.ع:

$W_{A \to O} (\vec{F}) = E_{p e} (A) - E_{p e} (O) W_{A \to O} (\vec{F}) = 2 . 10^{- 3} - 0 W_{A \to O} (\vec{F}) = 2 . 10^{- 3} J$