الامتحان الوطني الموحد 2015 الدورة العادية: الموضوع والتصحيح

1
التمرين 1
الكيمياء

الجزء الأول: التحليل الكهربائي لمحلول كلورور الصوديوم

يمكن التحليل الكهربائي من الحصول على غازات ذات نقاوة عالية

ننجز التحليل الكهربائي لمحلول مركز لكلورور الصوديوم $N a_{(a q)}^{+} + C l_{(a q)}^{-}$ , فيتكون على مستوى أحد الإلكترودين غاز ثنائي الكلور وعلى مستوى الإلكترود الاخر غاز ثنائي الهيدروجين, كما يصير الوسط التفاعلي قاعديا خلال التحول الكيميائي

معطيات:

المزدوجتان المتدخلتان في التحول الكيميائي:   $H_{2} O_{(l)} / H_{2 (g)}$ و $C l_{2_{(g)}} / C l_{(a q)}^{-}$

ثابتة فرادي: $1 F = 9, 65 . 10^{4} C . m o l^{- 1}$

الحجم المولي في ظروف التجربة: $V_{m} = 25, 0 L . m o l^{- 1}$

يمثل الشكل جانبه تبيانة التركيب التجريبي المستعمل لإنجاز هذا التحليل الكهربائي

$1$ حدد, معللا جوابك, من بين الإلكترودين $(A)$ و $(B)$ الإلكترود الذي يلعب دور الأنود والإلكترود الذي يلعب دور الكاثود

$2$ اكتب معادلة التفاعل الحاصل عند كل إلكترود والمعادلة الحصيلة

$3$ يزود المولد الدارة بتيار كهربائي شدته ثابتة $I = 3 A$

احسب حجم غاز ثنائي الكلور المتكون خلال المدة $∆ t = 25 m i n$

الجزء الثاني: دراسة تفاعل حمض البنزويك مع الماء ومع الإيثانول

يستعمل حمض البنزويك كمادة حافظة في تعليب بعض المواد الغذائية والمشروبات الغازية غير الكحولية. كما يدخل في تصنيع مجموعة من المركبات العضوية

يهدف هذا الجزء الى تحديد ثابتة الحمضية للمزدوجة $C_{6} H_{5} C O O H / C_{6} H_{5} C O O^{-}$ والى دراسة تفاعل حمض البنزويك مع الإيثانول

معطيات:

تمت القياسات عند درجة الحرارة $25 ° C$

الكتلة المولية لحمض البنزويك: $M (C_{6} H_{5} C O O H) = 122 g . m o l^{- 1}$

الكتلة المولية للإيثانول: $M (C_{2} H_{5} O H) = 46 g . m o l^{- 1}$

الكتلة الحجمية للإيثانول الخالص: $ρ = 0, 78 g . m L^{- 1}$

الكتلة المولية لبنزوات الإيثيل: $M (C_{6} H_{5} C O O C_{2} H_{5}) = 150 g . m o l^{- 1}$

الموصليتان الموليتان الأيونيتان: $λ_{C_{6} H_{5} C O O^{-}} = 3, 23 . 10^{- 3} S . m^{2} . m o l^{- 1}$ و $λ_{H_{3} O^{+}} = 35 . 10^{- 3} S . m^{2} . m o l^{- 1}$

تعبير الموصلية $σ$ لمحلول مخفف هو $σ = \sum_{i} λ_{i} . [X_{i}]$ حيث $[X_{i}]$ التركيز المولي الفعلي لكل نوع أيوني موجود في المحلول و $λ_{i}$ موصليته المولية الأيونية.

نهمل تأثير الأيونات $H O^{-}$ غير موصلية المحلول

$1$ دراسة تفاعل حمض البنزويك مع الماء

نعتبر محلولا مائيا $(S)$ لحمض البنزويك تركيزه المولي $C = 10 m o l . m^{- 3}$ وحجمه $V$

اعطى قياس موصلية المحلول $(S)$ القيمة   $σ = 2, 76 . 10^{- 2} S . m^{- 1}$ عند درجة الحرارة $25 ° C$

ننمذج التحول الكيميائي الذي يحدث بين حمض البنزويك والماء بالمعادلة الكيميائية التالية:

$C_{6} H_{5} C O O H_{(a q)} + H_{2} O_{(l)} ⇄ C_{6} H_{5} C O O {H^{-}}_{_{(a q)}} + H_{3} O_{_{(a q)}}^{+}$

$1 - 1$ بين أن نسبة التقدم النهائي $τ$ للتفاعل تساوي $0, 072$

$2 - 1$ أوجد تعبير خارج التفاعل $Q_{r, é q}$ عند التوازن بدلالة $C$ و $τ$

$3 - 1$ استنتج قيمة الثابتة $p K_{A}$ للمزدوجة $C_{6} H_{5} C O O H_{(a q)} / C_{6} H_{5} C O O_{_{(a q)}}^{-}$

$2$ دراسة تفاعل حمض البنزويك مع الإيثانول

يتميز بنزوات الإيثيل بنكهة فاكهة الكرز, لذا يستعمل في الصناعة الغذائية لإضفاء هذه النكهة على المواد الغذائية المصنعة

لتحضير بنزوات الإيثيل في المختبر, نمزج في حوجلة الكتلة $m_{a c} = 2, 44 g$ من حمض البنزويك مع الحجم   من الإيثانول الخالص ونضيف بعض القطرات من حمض الكبريتيك المركز الذي يلعب دور الحفاز, ثم نسخن بالارتداد الخليط التفاعلي تحت درجة حرارة ثابتة

$1 - 2$ ما دور الحفاز في هذا التفاعل؟

$2 - 2$ اكتب المعادلة الكيميائية المنمذجة للتحول الحاصل بين حمض البنزويك والإيثانول مستعملا الصيغ نصف المنشورة

$3 - 2$ تكونت عند نهاية التفاعل الكتلة $m_{e} = 2, 25 g$ من بنزوات الإيثيل. حدد قيمة $r$ مردود التفاعل

$4 - 2$ للرفع من مردود تفاعل تصنيع بنزوات الإيثيل, نعوض حمض البنزويك بمتفاعل اخر. اعط اسم هذا المتفاعل واكتب صيغته نصف المنشورة

الكيمياء

الجزء الأول: التحليل الكهربائي لمحلول كلورور الصوديوم

$1$ حسب تبيانة التركيب التجريبي منحى مرور الالكترونات عكس منحى التيار الكهربائي حيث تنتقل الإلكترونات من الإلكترود $B$ نحو الإلكترود $A$ (انظر الشكل جانبه)

الإلكترود $A$ يمثل الكاثود يحدث على مستواه اختزال (أي اكتساب $e^{-}$ )

الإلكترود $B$ يمثل الأنود تحدث على مستواه أكسدة (أي فقدان $e^{-}$ )

$2$ بجوار الكاثود يحدث اختزال جزيئة الماء:

$2 H_{2} O_{(l)} + 2 e^{-} ⇄ H_{2 (g)} + 2 H O_{(a q)}^{-}$

بجوار الأنود تحدث أكسدة أيون $C l^{-}$ الكلورور:

$2 C l_{(a q)}^{-} ⇄ C l_{2 (g)} + 2 e^{-}$

المعادلة الحصيلة:

$2 C l_{(a q)}^{-} + 2 H_{2} O_{(l)} ⇄ C l_{2 (g)} + H_{2} + 2 H O_{(a q)}^{-}$

$3$ حساب حجم غاز الكلور المتكون عند الأنود:

من خلال نصف المعادلة: $2 C l_{(a q)}^{-} ⇄ C l_{2 (g)} + 2 e^{-}$ لدينا: $n (C l_{2}) = \frac{n (e^{-})}{2}$

نعلم أن:

$\{\begin{cases} n (C l_{2}) = \frac{V (C l_{2})}{V_{m}} \\ n (e^{-}) = \frac{Q}{F} = \frac{I ∆ t}{F} \end{cases} \Rightarrow \frac{V (C l_{2})}{V_{m}} = \frac{I ∆ t}{2 F} \Rightarrow V (C l_{2}) = \frac{I ∆ t . V_{m}}{2 F}$

ت.ع:

$V (C l_{2}) = \frac{3 \times 25 \times 60 \times 25}{2 \times 9, 65 . 10^{4}} \approx 0, 58 L$

الجزء الثاني: دراسة تفاعل حمض البنزويك مع الماء ومع الإيثانول

$1$ دراسة تفاعل حمض البنزويك مع الماء

$1 - 1$ الجدول الوصفي للتفاعل الحاصل:

تعبير نسبة التقدم:

$τ = \frac{x_{é q}}{x_{m a x}}$

المتفاعل المحد هو الحمض:

$C . V - X_{m a x} = 0 \Rightarrow X_{m a x} = C . V$

حسب تعريف الموصلية:

$σ = λ_{C_{6} H_{5} C O O} - {[C_{6} H_{5} C O O^{-}]}_{é q} + λ_{H_{3} O} + {[H_{3} O^{+}]}_{é q}$

حسب الجدول الوصفي:

$σ = λ_{C_{6} H_{5} C O O} - {[H_{3} O^{+}]}_{é q} + λ_{(H_{3} O^{+})} {[H_{3} O^{+}]}_{é q} \Leftarrow {[A^{-}]}_{é q} = {[H_{3} O^{+}]}_{é q} = \frac{x_{é q}}{V}$

$x_{é q} = \frac{σ . V}{{λ_{C_{6} H_{5} C O O}}^{-} + λ_{(H_{3} O^{+})}} \Leftarrow ({λ_{C_{6} H_{5} C O O}}^{-} + λ_{(H_{3} O^{+})}) \frac{x_{é q}}{V}$

نسبة التقدم:

$τ = \frac{σ . V}{({λ_{C_{6} H_{5} C O O}}^{-} + λ_{(H_{3} O^{+)}}) . C . V} = \frac{σ}{({λ_{C_{6} H_{5} C O O}}^{-} + λ_{(H_{3} O^{+)}}) . C}$

ت.ع:

$τ = \frac{2, 76 . 10^{- 2}}{(3, 23 . 10^{- 3} + 35 . 10^{- 3}) \times 10} = 0, 072$

$2 - 1$ تعبير خارج التفاعل عند التوازن:

$Q_{r, é q} = \frac{{[A^{-}]}_{é q} {[H_{3} O^{+}]}_{é q}}{{[A H]}_{é q}}$

حسب الجدول الوصفي:

$\{\begin{cases} {[A^{-}]}_{é q} = {[H_{3} O^{+}]}_{é q} \\ {[A H]}_{é q} = \frac{C . V - x_{é q}}{V} = C - \frac{x_{é q}}{V} \end{cases} \Rightarrow \{\begin{cases} {[A^{-}]}_{é q} = {[H_{3} O^{+}]}_{é q} \\ {[A H]}_{é q} = C - {[H_{3} O^{+}]}_{é q} \end{cases} \Rightarrow \{\begin{cases} {[A^{-}]}_{é q} = {[H_{3} O^{+}]}_{é q} = c . τ \\ {[A H]}_{é q} = C - 10^{- p H} = C - C . τ \end{cases}$

$n_{0} (a l) = \frac{m_{a l}}{M (C_{2} H_{5} O H)} n_{0} (a l) = \frac{ρ . V}{M (C_{2} H_{5} O H)} n_{0} (a l) = \frac{0, 78 \times 10}{46} n_{0} (a l) = 0, 17 m o l$

$3 - 1$ استنتاج قيمة $p K_{A}$

لدينا: $Q_{r . é q} = K_{A}$ و $p K_{A} = - \log K_{A}$

$p K_{A} = \log \frac{C . τ^{2}}{1 - τ}$

$2$ دراسة تفاعل حمض البنزويك مع الإيثانول

$1 - 2$ دور حمض الكبريتيك (الحفاز) تسريع التفاعل

$2 - 2$ معادلة التفاعل بين حمض البنزويك و الإيثانول:

$C_{6} H_{5} - C O O H + C H_{3} - C H_{2} - O H ⇄ C_{6} H_{5} - C O O - C H_{2} - C H_{3} + H_{2} O$

$3 - 2$ تحديد مردود التفاعل:

حسب تعريف المردود:

$r = \frac{n_{e x p}}{n_{m a x}} = \frac{n_{e}}{x_{m a x}}$

حسب الجدول الوصفي:

$n_{0} (a c) = \frac{m_{a c}}{M (C_{6} H_{5} C O O H)} = \frac{2, 44}{122} = 0, 02 m o l$

$n_{0} (a l) = \frac{m_{a l}}{M (C_{2} H_{5} O H)} = \frac{ρ . V}{M (C_{2} H_{5} O H)} = \frac{0, 78 \times 10}{46} = 0, 17 m o l$

المتفاعل المحد هو حمض البنزويك و التقدم الأقصى $x_{m a x} = 0, 02 m o l$

$n_{e s t} = \frac{m_{e}}{M (C_{6} H_{5} C O O C_{2} H_{5})} = \frac{2, 25}{150} = 0, 015 m o l$

$r = \frac{n_{e s t}}{x_{m a x}} = \frac{0, 015}{0, 02} = 0, 75 \Rightarrow r = 75 %$

$4 - 2$ للرفع من مردود التفاعل نعوض حمض البنزويك بأندريد البنزويك صيغته نصف المنشورة هي:
2
التمرين 2
الموجات والتحولات النووية

يتضمن التمرين خمسة أسئلة, حيث تم اقتراح أربعة أجوبة لكل سؤال

انقل على ورقة التحرير رقم السؤال واكتب بجانبه الجواب الصحيح من بين الأجوبة الأربعة المقترحة دون إضافة أي تعليل أو تفسير

الموجات

تمكن الألياف البصرية من نقل المعلومات الرقمية بسرعة فائقة وبصبيب كبير مقارنة مع باقي الوسائط الأخرى

لتحديد معامل الانكسار للوسط الشفاف الذي يكون قلب ليف بصري, طوله $L$ , تم إنجاز تركيب تجريبي تبيانته ممثلة في الشكل $1$ , حيث يمكن اللاقطان $R_{1}$ و $R_{2}$ من تحويل الموجة الضوئية الأحادية اللون المنبعثة من جهاز اللازر الى توتر كهربائي نعاينه على شاشة راسم التذبذب كما هو مبين في الشكل $2$

معطيات:

الحساسية الأفقية: $0, 2 μ s / d i v$

سرعة الضوء في الفراغ: $c = 3 . 10^{8} m . s^{- 1}$

ثابتة بلانك: $h = 6, 63 . 10^{- 34} J . s$

$1$ التأخر الزمني $τ$ المسجل بين $R_{1}$ و $R_{2}$ هو:

$τ = 1, 0 m s ♦ τ = 1, 4 μ s ♦ τ = 1, 0 μ s ♦ τ = 0, 6 μ s ♦$

$2$ علما أن سرعة انتشار الموجة الضوئية في قلب الليف البصري تساوي $v \approx 1, 87 . 10^{8} m . s^{- 1}$ , إذن معامل الانكسار $n$ للوسط الشفاف الذي يكون قلب الليف البصري هو:

$n \approx 1, 7 ♦ n \approx 1, 6 ♦ n \approx 1, 5 ♦ n \approx 0, 63 ♦$

$3$ إذا كان طول موجة ضوء اللازر في الفراغ هو $λ = 530 n m$ , فإن قيمة طاقة فوتون واحد من هذا الإشعاع تساوي بالوحدة جول $(J)$ :

$E \approx 3, 75 . 10^{- 28} ♦ E \approx 37, 5 . 10^{- 19} ♦ E \approx 3, 75 . 10^{- 19} ♦ E \approx 1, 17 . 10^{- 48} ♦$

التحولات النووية

يستعمل الأستات $211$ , إشعاعي النشاط $a$ , في الطب النووي لتشخيص وتتبع تطور بعض الأورام السرطانية

ينتج عن تفتت نواة الأستات ${}_{85}^{211}A t$ النظير ${}_{y}^{x}B i$ لعنصر البيزموث

يمثل الشكل جانبه منحنى تغيرات $In (N)$ بدلالة الزمن $t$ , مع $N$ عدد نوى الأستات $211$ المتبقية عند اللحظة $t$

$4$ نواة البيزموث الناتجة عن تفتت النواة ${}_{85}^{211}A t$ هي:

${}_{84}^{208}B i ♦ {}_{83}^{207}B i ♦ {}_{82}^{207}B i ♦ {}_{83}^{206}B i ♦$

$5$ يساوي عمر النصف $t_{1 / 2}$ للأستات $211$ :

$t_{1 / 2} \approx 27, 30 h ♦ t_{1 / 2} \approx 7, 17 h ♦ t_{1 / 2} \approx 5, 50 h ♦ t_{1 / 2} \approx 4, 19 h ♦$

الموجات والتحولات النووية

تعليل أجوبة هذا التمرين ليس مطلوبا

الموجات

$1$ التأخر الزمني $τ$ هو $τ = 1 μ s$

التعليل:

$τ = \frac{0, 2 μ s}{d i v} \times 5 d i v = 1, 0 μ s$

$2$ معامل انكسار الوسط الشفاف $n$ هو $n \approx 1, 6$

التعليل:

$n = \frac{c}{v} = \frac{3 . 10^{8}}{1, 87 . 10^{8}} \approx 1, 6$

$3$ طاقة فوتون هذا الإشعاع هو $E \approx 3, 75 . 10^{- 19} J$

التعليل:

$E = h v = \frac{h c}{λ} E = \frac{6, 63 . 10^{- 34} \times 3 . 10^{8}}{530 . 10^{- 9}} E \approx 3, 75 . 10^{- 19} J$

التحولات النووية

$4$ نواة البزموت الناتجة عن تفتت النواة ${}_{83}^{211}A t$ رمزها هو ${}_{83}^{207}B i$

التعليل: باستعمال قانون صودي نحصل على معادلة التفتت التالية:

${}_{83}^{211}A t ⇄ {}_{83}^{207}B i + {}_{2}^{4}H e$

$5$ عمر النصف للاسيتات $211$ يساوي: $t_{1 / 2} \approx 7, 17 h$

التعليل:

قانون التناقص الاشعاعي:

$N = N_{0} e^{- λ t} \Rightarrow \log N = \log N_{0} - λ t \log N = \log N_{0} - \frac{I n 2}{t_{1 / 2}} t$

المعامل الموجه للدالة التالفية $L o g N = f (t)$ هو

$K = \frac{37, 65 - 37, 94}{3 - 0} = - \frac{i n 2}{t_{1 / 2}}$

$t_{1 / 2} = \frac{3 I n 2}{37, 94 - 37, 65} \approx 7, 17 h$
3
التمرين 3
الكهرباء

الجزء الأول: دراسة ثنائي القطب $R C$ خاضع لرتبة توتر صاعدة

تمكن المحارير الإلكترونية من قياس درجة الحرارة المرتفعة جدا التي لا يمكن قياسها بواسطة المحارير الكحولية أو الزئبقية. تعتمد بعض هذه المحارير في اشتغالها على تصرف ثنائي القطب $R C$ خاضع لرتبة توتر صاعدة, حيث تتغير المقاومة $R$ مع درجة الحرارة

لمعرفة العلاقة بين المقاومة الكهربائية $R$ ودرجة الحرارة $θ$ , أنجزت أستاذة الفيزياء تركيبا تجريبيا تبيانته ممثلة في الشكل $1$ والمكون من:

مكثف سعته $C = 1, 5 μ F$

مجس حراري, وهو عبارة عن ثنائي قطب مقاومته الكهربائية $R$ تتغير مع درجة الحرارة $θ$

مولد مؤمثل للتوتر, قوته الكهرمحركة $E = 6 V$

قاطع التيار $K$

وسيط معلوماتي يمكن من تتبع تطور التوتر $u_{c}$ بين مربطي المكثف بدلالة الزمن

بعد وضع المجس الحراري في وسط درجة حرارته $θ$ قابلة للضبط وغلق قاطع التيار $K$ , قامت الأستاذة بشحن المكثف عند درجات حرارة مختلفة, فحصلت على المنحنيات التجريبية الممثلة في الشكل $2$

$1 - 1$ انقل تبيانة الشكل $1$ على ورقة التحرير ومثل عليها التوتر بين مربطي المكثف $u_{c} (t)$ والتوتر بين مربطي المجس الحراري $u_{R} (t)$ في الاصطلاح مستقبل

$2 - 1$ أثبت المعادلة التفاضلية التي يحققها التوتر $u_{c} (t)$

$3 - 1$ يكتب حل هذه المعادلة التفاضلية على شكل $u_{c} (t) = A + B e^{- \frac{t}{R C}}$ , أوجد الثابتتين $A$ و $B$

$4 - 1$ حدد ثابتة الزمن $τ_{1}$ عند درجة الحرارة على مدة شحن المكثف

$5 - 1$ لقياس درجة الحرارة $θ_{2}$ لفرن كهربائي, وضعت الأستاذة المجس الحراري المدروس في الفرن, ثم حددت تجريبيا ثابتة الزمن $τ_{2}$ باستعمال نفس التركيب السابق (الشكل $1$ ), فوجدت القيمة $τ_{2} = 0, 45 m s$

يعطي منحنى الشكل $3$ تغيرات مقاومة المجس الحراري $R$ بدلالة درجة الحرارة $θ$

أوجد قيمة درجة الحرارة $θ_{2}$ داخل الفرن الكهربائي

الجزء الثاني: دراسة تضمين الوسع

نلجأ الى عملية التضمين لنقل المعلومات لمسافات كبيرة جدا بواسطة موجات كهرمغنطيسية. من بين المركبات الإلكترونية المعتمدة في تضمين الوسع, نستعمل دارة متكاملة منجزة للجداء

يهدف هذا الجزء من التمرين الى دراسة تضمين الوسع

خلال حصة الأشغال التطبيقية, طبقت مجموعة من التلاميذ توترا جيبيا تعبيره $u_{1} (t) = U_{0} + U_{m 1} \cos (2 πf t)$ عند المدخل $E_{1}$ لدارة متكاملة منجزة للجداء, حيث $U_{0}$ توتر المركبة المستمرة, وتوترا جيبيا تعبيره $u_{2} (t) = U_{m 2} \cos (2 π F t)$ الموافق لموجة حاملة عند المدخل $E_{2}$ . (الشكل $4$ )

$1 - 2$ يكون تعبير التوتر $u_{s} (t)$ عند مخرج الدارة المتكاملة هو: $u_{s} (t) = k . u_{1} (t) . u_{2} (t)$ , مع $K$ ثابتة تتعلق بالدارة المتكاملة

بين أن وسع التوتر $u_{s} (t)$ يكتب على الشكل: $U_{s} = A [1 + m . \cos (2 π f t)]$ محددا تعبير كل من $A$ و $m$

$2 - 2$ بعد ضبط كاشف التذبذب على الحساسيتين $1 V / d i v$ و $0, 5 m s / d i v$ , عاين التلاميذ توتر الخروج $u_{s} (t)$ المحصل عليه والممثل في الشكل $5$

حدد التردد $f$ للإشارة المضمنة والتردد $F$ للموجة الحاملة

$3 - 2$ بحساب نسبة التضمين $m$ , بين أن التضمين جيد

الكهرباء

الجزء الأول: دراسة ثنائي القطب $R C$ خاضع لرتبة توتر صاعدة

$1 - 1$ تمثيل التوترين $u_{c}$ و $u_{R}$ في اصطلاح مستقبل

$2 - 1$ إثبات المعادلة التفاضلية التي يحققها التوتر $u_{c}$

حسب قانون إضافية التوترات: $u_{R} + u_{c} = E$

$R i + u_{c} = E$ مع: $i = \frac{d q}{d t} = C \frac{d u_{c}}{d t}$

$R C \frac{d u_{c}}{d t} + u_{c} = E$

المعادلة التفاضلية تكتب:

$τ \frac{d u_{c}}{d t} + u_{c} = E$

مع: $τ = R C$

$3 - 1$ تعبير كل من $A$ و $B$

لدينا:

$\{\begin{cases} u_{c} = A + B e^{- t /_{R C}} \\ \frac{d u_{c}}{d t} = - \frac{B}{R C} e^{- t /_{R C}} \end{cases}$

نعوض في المعادلة التفاضلية:

$- R C \frac{B}{R C} e^{-^{t} / R C} + A + B e^{^{-^{t} / R C}} = E \Rightarrow A - E + B e^{^{-^{t} / τ}} (1 - 1) = 0 \Rightarrow A = E$

حسب الشروط البدئية: $u_{c} (0) = A + B = 0 \Rightarrow B = - A \Rightarrow B = - E$

حل المعادلة التفاضلية يكتب:

$u_{c} (t) = E (1 - e^{-^{t} / τ})$

$4 - 1$ تحديد ثابتة الزمن $τ_{1}$ عند درجة الحرارة $205 ° C$

عند اللحظة $t = τ$ نكتب: $u_{c} (τ) = E (1 - e^{- 1}) = 6 (1 - e^{- 1}) = 3, 79 V$

مبيانيا (انظر الشكل $2$ ) نجد: $τ_{1} = 0, 5 m s$

كلما ارتفعت درجة الحرارة $θ$ كلما تناقصت قيمة $τ$ وبالتالي تناقصت مدة الشحن

$5 - 1$ تحديد درجة الحرارة $θ_{2}$

تحديد مقاومة المجس الحراري $R_{2}$ الموافق لقيمة $τ_{2}$ حيث: $τ_{2} = R_{2} . C$ أي: $R_{2} = \frac{τ_{2}}{C}$

$R_{2} = \frac{0, 45 . 10^{- 3}}{1, 5 . 10^{- 6}} = 300 Ω = 0, 3 k Ω$

باستعمال مبيان الشكل $3$ نجد: $θ_{2} = 210 ° C$

الجزء الثاني: دراسة تضمين الوسع

$1 - 2$ إثبات تعبير وسع التوتر المضمن الوسع $U_{s} (t)$

لدينا:

$U_{s} (t) = K . u_{1} (t) . u_{2} (t) U_{s} (t) = K [U_{0} + U_{m 1} \cos (2 πft)] U_{m 2} \cos (2 π F t)$

نضع:

$U_{s} (t) = k . U_{0} . U_{m 2} [1 + \frac{U_{m 2}}{U_{0}} \cos (2 πft)] \cos (2 π F t)$

$2 - 2$ تحديد التردد $f$ و $F$

حسب الشكل $5$ الدور $T_{s}$ يساوي: $T_{s} = 8 d i v \times 0, 5 m s . d i v^{- 1}$

التردد $f$ :

$f = \frac{1}{T_{s}} = \frac{1}{8 \times 0, 5 \times 10^{- 3}} = 250 H z$

الدور $T_{p}$ يساوي: $T_{s} = 20 T_{p}$

التردد $F$ : $\frac{1}{f} = 20 \times \frac{1}{F}$

أي: $F = 20 f = 20 \times 250 = 5 . 10^{4} H z$

$F = 50 k H z$

$3 - 2$ حساب نسبة التضمين $m$

$m = \frac{U m m a x - U_{m m i n}}{U_{m} m a x + U_{m m i n}}$

حسب الشكل $5$ :

$\{\begin{cases} U_{m m i n} = 1 V / d i v \times 1 d i v = 1 V \\ U_{m m i n} = 1 V / d i v \times 5 d i v = 5 V \end{cases} \Rightarrow m = \frac{5 - 1}{5 + 1} = 0, 67$

بما أن $m < 1$ فإن التضمين جيد
4
التمرين 4
الميكانيك

الجزء الأول: دراسة حركة كرة الغولف في مجال الثقالة المنتظم

يتكون أحد مدارات ملعب الغولف من ثلاثة اجزاء:

جزء أفقي $OA$ طوله $OA = 2, 2 m$

جزء $AB$ طوله $AB = 4 m$ ومائل بزاوية $a = 24 °$ بالنسبة للمستوى الأفقي

جزء $BC$ أفقي به حفرة مركزها $T$ يبعد عن النقطة $B$ بالمسافة $BT = 2, 1 m$

توجد النقط $B$ و $T$ و $C$ على الاستقامة واحدة

نهمل تأثير الهواء وأبعاد كرة الغولف

نأخذ $g = 10 m . s^{- 2}$

تتم دراسة حركة الكرة في المعلم $(O, \vec{i}, \vec{j})$ المرتبط بالأرض والذي نعتبره غاليليا

عند اللحظة $t = 0$ , تم إرسال كرة الغولف من النقطة $O$ نحو المركز $T$ للحفرة بسرعة بدئية $V_{0} = 10 m . s^{- 1}$ تكون المتجهة $\bar{V_{0}}$ زاوية $θ = 45 °$ مع المحور الأفقي $(O x)$ . (الشكل $1$ )

$1$ بتطبيق القانون الثاني لنيوتن, أوجد المعادلتين الزمنيتين $x (t)$ و $y (t)$ لحركة الكرة

$2$ استنتج معادلة مسار الكرة

$3$ حدد قيمة $x_{s}$ أفصول قمة مسار الكرة

$4$ تحقق من أن الكرة تمر من النقطة $T$ مركز الحفرة

الجزء الثاني: دراسة متذبذب أفقي

ندرس في هذا الجزء تذبذبات مجموعة ميكانيكية (جسم صلب-نابض) في وضعية تكون فيها الاحتكاكات المائعة غير مهملة

نعتبر جسما صلبا $(S)$ , كتلته $m$ ومركز قصوره $G$ , مثبتا بطرف نابض كتلته مهملة ولفاته غير متصلة وصلابته $K = 20 N . m^{- 1}$ . الطرف الاخر للنابض مرتبط في النقطة $A$ بحامل ثابت

بواسطة ساق, نثبت صفيحة بالجسم $(S)$ ثم نغمر جزءا منها في سائل لزج كما يبين الشكل $2$

نهمل كتلة كل من الساق والصفيحة أمام كتلة الجسم $(S)$

نمعلم موضع $G$ عند اللحظة $t$ بالأفصول $x$ على المحور $(O x)$

يطابق أفصول $G_{0}$ موضع $G$ عند التوازن النقطة $O$ أصل المحور $(O x)$

ندرس حركة $G$ في معلم أرضي نعتبره غاليليا

نختار الموضع $G_{0}$ مرجعا لطاقة الوضع المرنة للمتذبذب والمستوى الأفقي المار من $G$ مرجعا لطاقة الوضع الثقالية

يكون النابض غير مشوه عند التوازن

نزيح الجسم $(S)$ بمسافة $d$ عن موضع توازنه ثم نحرره بدون سرعة بدئية

مكن جهاز مسك معلوماتي مناسب من خط منحنى تغيرات أفصول مركز القصور $G$ بدلالة الزمن, الشكل $3$

$1$ أي نظام للتذبذب يبرزه المنحنى الممثل في الشكل $3$ ؟

$2$ بحساب تغير طاقة الوضع المرنة للمتذبذب بين اللحظتين $t_{0} = 0$ و $t_{1} = 1, 2 s$ , أوجد الشغل $W (\bar{F})$ لقوة الارتداد التي يطبقها النابض بين هاتين اللحظتين

$3$ حدد تغير الطاقة الميكانيكية $∆ E_{m}$ للمجموعة بين اللحظتين $t_{0}$ و $t_{1}$ وأعط تفسيرا للنتيجة المحصل عليها

الميكانيك

الجزء الأول: دراسة حركة كرة الغولف في مجال الثقالة المنتظم

$1$ المعادلتين الزمنيتين $x (t)$ و $y (t)$

المجموعة المدروسة: {كرة الغولف}

تخضع الكرة لقوة وحيدة $\vec{P}$

باعتبار المعلم $(O, \vec{i}, \vec{j})$ المرتبط بالأرض غاليليا, نطبق القانون الثاني لنيوتن نكتب: $m {\vec{a}}_{G} = \vec{P}$ أي: $m {\vec{a}}_{G} = m \vec{g}$ وبالتالي:

${\vec{a}}_{G} = \vec{g}$
حسب الشروط البدئية:   $\{\begin{cases} x_{0} = 0 \\ y_{0} = 0 \end{cases}$ و $\{\begin{cases} V_{0 x} = v_{0} \cos θ \\ V_{0 y} = v_{0} \sin θ \end{cases}$

الاسقاط على $O x$ و $O y$ :

${\vec{a}}_{G} |\begin{matrix} a_{x} = 0 \\ a_{y} = - g \end{matrix} \Rightarrow| \begin{matrix} a_{x} = \frac{d V_{x}}{d t} = 0 \\ a_{y} = \frac{d V_{x}}{d t} = الحفرة مركز - g \end{matrix}$

$\overset{تـكـامـل}{\to} \begin{matrix} V_{x} = V_{0 x} = V_{0} \cos θ \\ V_{y} = - g t + V_{0 y} = - g t + V_{0} \sin θ \end{matrix}$

$\overset{تـكـامـل}{\to} \vec{O G} \begin{matrix} x (t) = V_{0} \cos θ . t + x_{0} \\ y (t) = - \frac{1}{2} g t^{2} + V_{0} \sin θ . t + y_{0} \end{matrix}$

$\overset{الزمنيتين المعادلتين}{\to} \{\begin{cases} x (t) = V_{0} \cos θ . t \\ y (t) = - \frac{1}{2} g t^{2} + V_{0} \sin θ . t \end{cases}$

${\vec{v}}_{G} \begin{matrix} V_{x} = \frac{d x}{d t} = V_{0} \cos θ \\ V_{y} = \frac{d y}{d t} = - g t + V_{0} \sin θ \end{matrix}$

ت.ع:

$\{\begin{cases} x (t) = 10 \times \cos (45 °) . \Rightarrow x (t) = 7, 07 t \\ y (t) = - \frac{1}{2} \times 10 . t^{2} + 10 \sin (45 °) . t = 5 t^{2} + 7, 07 t \end{cases}$

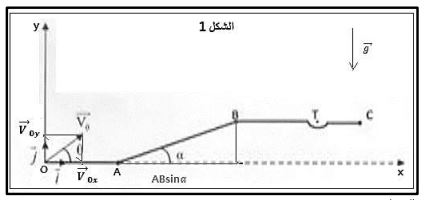
$2$ استنتاج معادلة المسار

لنحدد معادلة المسار بإقصاء الزمن من المعادلتين الزمنيتين:

$t = \frac{x}{V_{0} \cos θ} \Rightarrow y = - \frac{1}{2} g {(\frac{x}{V_{0} \cos θ})}^{2} + V_{0} \sin θ . \frac{x}{V_{0} \cos θ} \Rightarrow y = - \frac{g}{2 V_{0}^{2} \cos^{2} θ} x^{2} + x . \tan θ$

ت.ع:

$y = - \frac{10}{2 \times 10^{2} \times \cos^{2} (45 °)} . x^{2} + x . \tan (45 °) \Rightarrow y = - 0, 1 x^{2} + x$

$3$ تحديد $x_{s}$ أفصول قيمة المسار

عند قمة المسار يكون:

$\frac{d y}{d x} = 0 \Rightarrow - 2 \times (0, 1) x + 1 = 0 \Rightarrow - 0, 2 x = - 1 \Rightarrow x = x_{s} = \frac{1}{0, 2} = 5 m$

$4$ التحقق من أن الكرة تمر من النقطة $T$

إحداثيات النقطة $T$ هما:

$\{\begin{cases} x_{T} = O A + A B . \cos a + B T = 2, 2 + 4 \cos (24 °) + 2, 1 = 7, 95 m \\ y_{T} = A B . \sin a = 4 \sin (24 °) = 1, 63 m \end{cases}$

نحدد أرتوب النقطة $P$ باستعمال معادلة المسار:

$y (x_{p}) = - 0, 1 \times {(7, 95)}^{2} + 7, 95 \Rightarrow y (x_{p}) = y_{p} = 1, 63 m$

نستنتج أن الكرة تمر من النقطة $T$ مركز الحفرة

الجزء الثاني: دراسة متذبذب أفقي

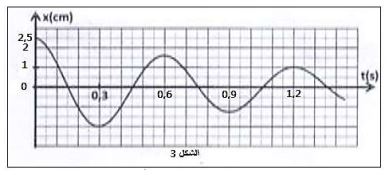
$1$ نظام التذبذبات شبه دوري

$2$ حساب تغير طاقة الوضع المرنة $∆ E_{p e}$ للمتذبذب بين اللحظتين $t_{0} = 0$ و $t_{1}$

لدينا:

$∆ E_{p e} = E_{p e} (t_{1}) - E_{p e} (t_{0}) ∆ E_{p e} = \frac{1}{2} K x_{1}^{2} + C - (\frac{1}{2} K x_{0}^{2} + C) ∆ E_{p e} = \frac{1}{2} K (x_{1}^{2} - x_{0}^{2})$

مبيانيا لدينا عند $x_{1} = 1 c m = 10^{- 2} m \leftarrow t_{1} = 1, 2 s$

وعند   $x_{0} = 2, 5 c m = 2, 5 . 10^{- 2} m \leftarrow t_{0} = 0$

ت.ع:

$∆ E_{p e} = \frac{1}{2} \times 20 \times \{{[(1 . 10^{- 2})]}^{2} - {[(2, 5 . 10^{- 2}]}^{2}\} {[(1 . 10^{- 2})]}^{2} - {[(2, 5 . 10^{- 2}]}^{2} ∆ E_{p e} = = - 5, 25 . 10^{- 3} J \Rightarrow ∆ E_{p e} = - 5, 25 m J$

استنتاج شغل قوة الارتداد: $W (\vec{T})$

$W (\vec{T}) = - ∆ E_{p e} = 5, 25 m J$

$3$ تحديد $∆ E_{m}$ تغير الطاقة الميكانيكية

لدينا: $E_{m} = E_{c} + E_{p e}$

عندما تكون طاقة الوضع المرنة قصوية, تكون الطاقة الحركية منعدمة والعكس

عند اللحظة $x_{1} = 1 c m \leftarrow t_{1}$ تكون $E_{p e 1 m a x}$ والسرعة $V_{1} = 0$ وبالتالي:   $E_{c_{1}} = 0$

عند اللحظة $x_{0} = 2, 5 c m \leftarrow t_{0}$ تكون $E_{p e 0 m a x}$ والسرعة $V_{0} = 0$ وبالتالي: $E_{c_{0}} = 0$

$∆ E_{m} = ∆ E_{c} + ∆ E_{p} ∆ E_{m} = ∆ E_{p e} ∆ E_{m} = - 5, 25 m J < 0$

التفسير:

في حالة خمود غير مهمل, (فإن الطاقة الميكانيكية لا تنحفظ) تتناقص $E_{m}$ حيث تتحول الطاقة الميكانيكية حرارية بفعل شغل قوى الاحتكاك

$∆ E_{m} = W (f) < 0$