المسألة: دراسة دالة عددية وحساب التكامل والمتتاليات العددية
تحديد
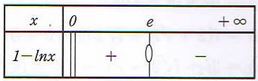
إذن يقبل مقاربا عموديا معادلته
إذن يقبل مقاربا أفقيا معادلته بجوار
إذن يقبل مقاربا عموديا معادلته
لدينا دالة قابلة للاشتقاق على ولدينا لكل من
لدينا
ومنه إشارة هي إشارة على

إذن الدالة تناقصية على المجال وتزايدية على كل من المجالين و
جدول تغيرات الدالة على هو
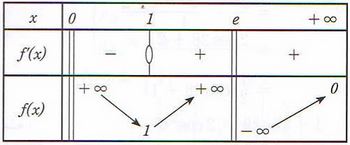
المعادلة مبيانيا تعني تحديد أفاصيل نقط تقاطع مع محور الأفاصيل
بما أن يقطع محور الأفاصيل في نقطتين، فإن عدد حلول المعادلة هو
لدينا دالة متصلة كمجموع وجداء دوال متصلة على
ولدينا تزايدية قطعا على و و
إذن حسب مبرهنة القيم الوسيطية المعادلة تقبل حلا بحيث
ليكن من
ليكن من
تحديد تقاطع والمستقيم يعني تحديد حلول المعادلة
إذن المستقيم الذي معادلته يقطع المنحنى في النقطتين اللتين أفصولهما و
انطلاقا من ، لدينا
ليكن
إذن لكل من
إنشاء المستقيم والمنحنى
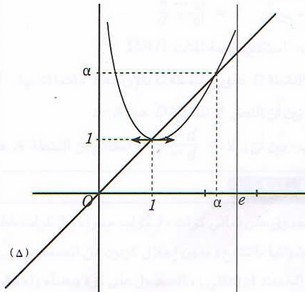
لدينا
المساحة المطلوبة هي
لنبين بالترجع أن لكل من
نفترض أن ولنبين أن
لدينا و تزايدية على
إذن
و بما أن و و
فإن
وبالتالي لكل من
حسب نتيجة السؤال لدينا
وبما أن فإن
أي
ومنه المتتالية تناقصية
بما أن مصغورة بالعدد فإنها متقاربة
لدينا و و متصلة على و
إذن نهاية هي بحيث هو حل المعادلة
بما أن تناقصية فإنها مكبورة بحدها الأول أي
وبالتالي