الامتحان الوطني الموحد 2015 الدورة العادية: الموضوع والتصحيح

1

التمرين 1

الأعداد العقدية

$1$ نعتبر في المجموعة $ℂ$ المعادلة التالية:

$(E) : z^{2} - (5 + i \sqrt{3}) z + 4 + 4 i \sqrt{3} = 0$

$أ$ تحقق أن ${(3 - i \sqrt{3})}^{2}$ هو مميز المعادلة $(E)$

$ب$ حدد $a$ و $b$ حلي المعادلة $(E)$ (علما أن $b \in ℝ$ )

$ج$ تحقق أن $b = (1 - i \sqrt{3}) a$

$2$ المستوى العقدي منسوب إلى معلم متعامد ممنظم مباشر

لتكن $A$ النقطة التي لحقها $a$ و $B$ النقطة التي لحقها $b$

$أ$ حدد العدد العقدي $b_{1}$ لحق النقطة $B_{1}$ صورة النقطة $O$ بالدوران الذي مركزه $A$ وزاويته $\frac{p}{2}$

$ب$ بين أن $B$ هي صورة $B_{1}$ بالتحاكي الذي مركزه $A$ ونسبته $\frac{p}{2}$

$ج$ تحقق أن: $a r g (\frac{b}{b - a}) \equiv \frac{π}{6} [2 π]$

$د$ لتكن $C$ نقطة، لحقها $c$ ، تنتمي إلى الدائرة المحيطة بالمثلث $O A B$ وتخالف $O$ و $A$

حدد عمدة للعدد العقدي $\frac{c}{c - a}$

الأعداد العقدية

$1$ لدينا $(E) : z^{2} - (5 + i \sqrt{3}) z + 4 + 4 i \sqrt{3} = 0$

$أ$

$Δ = {(5 + i \sqrt{3})}^{2} - 4 (4 + 4 i \sqrt{3}) Δ = 25 + 10 i \sqrt{3} - 3 - 16 i \sqrt{3} Δ = 6 - 6 i \sqrt{3} Δ = 9 - 6 i \sqrt{3} - 3 Δ = {(3 - i \sqrt{3})}^{2}$

$ب$

$\{\begin{cases} a = \frac{5 + i \sqrt{3} - 3 + i \sqrt{3}}{2} = 1 + i \sqrt{3} \\ b = \frac{5 + i \sqrt{3} + 3 - i \sqrt{3}}{2} = 4 \end{cases}$

$ج$

لدينا $a (1 - i \sqrt{3}) = (1 + i \sqrt{3}) . (1 - i \sqrt{3}) = 1 + 3 = 4 = b$

إذن

$b = (1 - i \sqrt{3}) a$

$2$

$أ$

الصيغة العقدية للدوران $R (A, \frac{π}{2})$ هي $z' = e^{\frac{π}{2} i} (z - a) + a = i (z - a) + a$

بما أن $B_{1} = R (O)$ فإن

$b_{1} = i (0 - a) + a b_{1} = - i a + a b_{1} = - i (1 + i \sqrt{3}) + 1 + i \sqrt{3} b_{1} = - i - \sqrt{3} + 1 + i \sqrt{3} b_{1} = 1 - \sqrt{3} + i (\sqrt{3} - 1)$

$ب$

الصيغة العقدية للتحاكي $h$ هي $z' = k (z - a) + a = \sqrt{3} (z - a) + a$

لتكن $B_{1}' = R (B_{1})$

$b_{1}' = \sqrt{3} (b_{1} - a) + a b_{1}' = \sqrt{3} (- i a) + a b_{1}' = a (1 - i \sqrt{3}) b_{1}' = b \Rightarrow B_{1}' = B$

ومنه

$B = R (B_{1})$

$ج$

لدينا

$A = \frac{b}{b - a} = \frac{b}{a - i \sqrt{3} a - a} A = \frac{b}{- a \sqrt{3} i} A = \frac{\frac{b}{a}}{- \sqrt{3} i} A = \frac{1 - i \sqrt{3}}{- \sqrt{3} i} A = \frac{2}{\sqrt{3}} \frac{(\frac{1}{2} - \frac{\sqrt{3}}{2} i)}{- i} A = \frac{2}{\sqrt{3}} \frac{e^{\frac{- π}{3} i}}{e^{\frac{π}{2} i}} A = \frac{b}{b - a} = \frac{2}{\sqrt{3}} e^{\frac{π}{6} i}$

وبالتالي $a r g (\frac{b}{b - a}) \equiv \frac{π}{6} [2 π]$

$د$

بما أن $C$ تنتمي إلى الدائرة المحيطة بالمثلث $O A B$ فإن النقط $O$ و $A$ و $B$ و $C$ متداورة

ومنه

$\frac{c - 0}{c - a} + \frac{b - 0}{b - a} \in ℝ \Rightarrow a r g (\frac{c - 0}{c - a} + \frac{b - 0}{b - a}) \equiv 0 [π] \Rightarrow a r g (\frac{c}{c - a}) - a r g (\frac{b}{b - a}) \equiv 0 [π]$

إذن

$a r g (\frac{c}{c - a}) \equiv \frac{π}{6} [π]$
2

التمرين 2

الحسابيات

ليكن $x$ عددا صحيحا نسبيا بحيث $x^{1439} \equiv 1436 [2015]$

$1$ علما أن $1436 \times 1051 - 2015 \times 749 = 1$ ،بين أن $1436$ و $2015$ أوليان فيما بينهما

$2$ ليكن $d$ قاسما مشتركا للعددين $x$ و $2015$

$أ$ بين أن $d$ يقسم $1436$

$ب$ استنتج أن $x$ و $2015$ أوليان فيما بينهما

$3$

$أ$ باستعمال مبرهنة فيرما بين أن $x^{1440} \equiv 1 [5]$ و $x^{1440} \equiv 1 [13]$ و $x^{1440} \equiv 1 [31]$

(لاحظ أن $2015 = 5 \times 13 \times 31$ )

$ب$ بين أن $x^{1440} \equiv 1 [65]$ ثم استنتج أن $x^{1440} \equiv 1 [2015]$

$4$ بين أن $x \equiv 1051 [2015]$

الحسابيات

$1$ بما أن $1436 \times 1051 - 2015 \times 749 = 1$ فحسب مبرهنة بيزو $" B e z o u t "$ فإن $1436 \land 2015 = 1$

$2$

$أ$ لدينا $x^{1439} \equiv 1436 [2015]$

إذن $\exists k \in ℤ / x^{1439} - 2015 k = 1436$

لدينا $d / x$ و $d / 2015$

ومنه $d / x^{1436}$ و $d / 2015 k$

وبالتالي $d / x^{1436} - 2015 k$

$d / 1436$

$ب$ نضع $x \land 2015 = d$

إذن $d / x$ و $d / 2015$

وبالتالي وحسب السؤال السابق $d / 1436$

إذن $d / 1436 \times 1051$

ولدينا

$d / 2015 \Rightarrow d / 2015 \times 749 \Rightarrow d / 1436 \times 1051 - 2015 \times 749 \Rightarrow d / 1$

وبما أن $d > 0$ فإن $d = 1$ وبالتالي

$x \land 2015 = 1$

$3$

$أ$ لدينا

$x \land 2015 = 1 \Rightarrow x \land (5 \times 13 \times 31) = 1 \Rightarrow (\begin{matrix} x \land 5 = 1 \\ x \land 13 = 1 \\ x \land 31 = 1 \end{matrix})$

إذن باستعمال مبرهنة فيرما

$(\begin{matrix} x^{4} \equiv 1 [5] \\ x^{12} \equiv 1 [13] \\ x^{30} \equiv 1 [31] \end{matrix}) \Rightarrow (\begin{matrix} {(x^{4})}^{360} \equiv 1 [5] \\ {(x^{12})}^{120} \equiv 1 [13] \\ {(x^{30})}^{48} \equiv 1 [31] \end{matrix}) \Rightarrow (\begin{matrix} x^{1404} \equiv 1 [5] \\ x^{1404} \equiv 1 [13] \\ x^{1404} \equiv 1 [31] \end{matrix})$

$ب$ لدينا

$\{\begin{cases} x^{1404} \equiv 1 [5] \\ x^{1404} \equiv 1 [13] \end{cases} \Rightarrow \{\begin{cases} 5 / x^{1404} - 1 \\ 13 / x^{1404} - 1 \end{cases} \Rightarrow (5 \lor 13) / x^{1404} - 1 \Rightarrow 65 / x^{1404} - 1 \Rightarrow x^{1404} \equiv 1 [65]$

ولدينا

$\{\begin{cases} x^{1404} \equiv 1 [65] \\ x^{1404} \equiv 1 [31] \end{cases} \Rightarrow \{\begin{cases} 65 / x^{1404} - 1 \\ 31 / x^{1404} - 1 \end{cases} \Rightarrow (65 \lor 31) / x^{1404} - 1 \Rightarrow 2015 / x^{1404} - 1 \Rightarrow x^{1404} \equiv 1 [2015]$

$4$

لدينا

$x^{1439} \equiv 1436 [2015] \Rightarrow x^{1440} \equiv 1436 x [2015]$

ولدينا $x^{1404} \equiv 1 [2015]$

إذن

$1436 x \equiv 1 [2015] \Rightarrow \exists α \in ℤ / 1436 x - 2015 α = 1 \Rightarrow 1436 x - 2015 α = 1436 \times 1051 - 2015 \times 749 \Rightarrow 1436 (x - 1051) = 2015 (α - 749) \Rightarrow 2015 / 1436 (x - 1051)$

وبما أن $2015 \land 1436 = 1$ فإن $2015 / (x - 1051)$ وبالتالي

$x \equiv 1051 [2015]$
3

التمرين 3

البنيات الجبرية

نذكر أن $(M_{2} (ℝ), +, \times)$ حلقة واحدية وحدتها $I = (\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix})$ وأن $(ℝ, +)$ زمرة تبادلية

لكل عدد حقيقي $x$ نضع $M (x) = (\begin{matrix} 1 - x & x \\ - 2 x & 1 + 2 x \end{matrix})$ ونعتبر المجموعة $E = \{M (x) / x \in ℝ\}$

نزود $E$ بقانون التركيب الداخلي $T$ المعرف بما يلي

$(\forall (x, y) \in ℝ^{2}) M (x) T M (y) = M (x + y + 1)$

$1$ ليكن $φ$ التطبيق من $ℝ$ نحو $E$ المعرف بما يلي $(\forall x \in ℝ) φ (x) = M (x - 1)$

$أ$ بين أن $φ$ تشاكل من $(ℝ, +)$ نحو $(E, T)$

$ب$ بين أن $(E, T)$ زمرة تبادلية

$2$

$أ$ بين أن $(\forall (x, y) \in ℝ^{2}) M (x) \times M (y) = M (x + y + x y)$

$ب$ استنتج أن $E$ جزء مستقر من $(M_{2} (ℝ), \times)$ وأن القانون $" \times "$ تبادلي في $E$

$ج$ بين أن القانون $" \times "$ توزيعي بالنسبة للقانون $" T "$ في $E$

$د$ تحقق أن $M (- 1)$ هو العنصر المحايد في $(E, T)$ وأن $I$ هو العنصر المحايد في $(E, \times)$

$3$

$أ$ تحقق أن $(\forall x \in ℝ - \{- 1\}) M (x) \times M (\frac{- x}{1 + x}) = I$

$ب$ بين أن $(E, T, \times)$ جسم تبادلي

البنيات الجبرية

$1$

$أ$

$(\forall (x, y) \in ℝ^{2}) φ (x + y) = M (x + y - 1) φ (x) T φ (y) = M (x - 1) T M (y - 1) φ (x) T φ (y) = M (x - 1 + y - 1 + 1) φ (x) T φ (y) = M (x + y - 1) φ (x) T φ (y) = φ (x + y)$

إذن $φ$ تشاكل من $(ℝ, +)$ نحو $(E, T)$

$ب$ لدينا

$(\forall x \in ℝ) φ (x + 1) = M (x) \Rightarrow (\forall M \in E) (\exists m \in ℝ) φ (m) = M \Rightarrow φ (ℝ) = E$

وبما أن $(ℝ, +)$ زمرة تبادلية فإن $(E, T)$ زمرة تبادلية عنصرها المحايد هو $φ (0) = M (- 1)$

$2$

$أ$

$(\forall (x, y) \in ℝ^{2}) M (x) \times M (y) = (\begin{matrix} 1 - x & x \\ - 2 x & 1 + 2 x \end{matrix}) \times (\begin{matrix} 1 - y & y \\ - 2 y & 1 + 2 y \end{matrix}) = (\begin{matrix} (1 - x) (1 - y) - 2 x y & y (1 - x) + x (1 + 2 y) \\ - 2 x (1 - y) - 2 y (1 + 2 x) & - 2 x y + (1 + 2 x) (1 + 2 y) \end{matrix}) = (\begin{matrix} 1 - x - y - x y & x + y + x y \\ - 2 x - 2 y - 2 x y & 1 + 2 y + 2 x + 2 x y \end{matrix}) = (\begin{matrix} 1 - (x + y + x y) & x + y + x y \\ - 2 (x + y + x y) & 1 + 2 (x + y + x y) \end{matrix}) M (x) \times M (y) = M (x + y + x y)$

$ب$

بما أن $(x, y) \in ℝ^{2} \Rightarrow x + y + x y \in ℝ$

فإن

$(M (x), M (y)) \in E^{2} \Rightarrow M (x + y + x y) \in E \Rightarrow M (x) \times M (y) \in E$

إذن $E$ جزء مستقر من $(M_{2} (ℝ), \times)$ , ولدينا أيضا

$(\forall (x, y) \in ℝ^{2}) M (x) \times M (y) = M (x + y + x y) = M (y + x + y x) = M (y) \times M (x)$

إذن القانون $" \times "$ تبادلي في $E$

$ج$ لدينا لكل $(x, y, z) \in ℝ^{3}$

$A = M (x) \times (M (y) T M (z)) A = M (x) \times M (y + z + 1) A = M (x + y + z + 1 + x (y + z + 1)) A = M (x + y + z + 1 + x y + x z + x) A = M (2 x + y + z + x y + x z + 1)$

و

$B = (M (x) \times M (y)) T (M (x) \times M (z)) B = M (x + y + 1) T M (x + z + 1) B = M (x + y + x y + x + z + x z + 1) B = M (2 x + y + z + x y + x z + 1) B = A$

إذن القانون $" \times "$ توزيعي بالنسبة للقانون $" T "$ في $E$

$د$ لدينا $(\forall x \in ℝ) M (x) T M (- 1) = M (x - 1 + 1) = M (x)$

إذن $M (- 1)$ هو العنصر المحايد في $(E, T)$

ولدينا $M (0) = I$ و $(\forall x \in ℝ) M (x) \times M (0) = M (x + 0 + 0) = M (x)$

إذن $I$ هو العنصر المحايد في $(E, \times)$

$3$

$أ$ لدينا

$(\forall x \in ℝ - \{- 1\}) M (x) \times M (\frac{- x}{1 + x}) = M (x - \frac{x}{1 + x} - \frac{x^{2}}{1 + x}) M (x) \times M (\frac{- x}{1 + x}) = M (\frac{x + x^{2} - x - x^{2}}{1 + x}) M (x) \times M (\frac{- x}{1 + x}) = M (0) = I$

$ب$ لدينا $(E, T)$ زمرة تبادلية عنصرها المحايد هو $M (- 1)$

القانون $" \times "$ قانون تركيب داخلي تبادلي في $E$ وتجميعي لأن $E \subset M_{2} (ℝ)$ و $(M_{2} (ℝ), \times)$ تجميعي

القانون $" \times "$ توزيعي بالنسبة ل $T$ في $E$ وله عنصر محايد هو $M (0) = I$

إذن $(E, T, \times)$ حلقة واحدية، وبما أن لكل $M (x) \in E - \{M (- 1)\}$ مماثلا بالنسبة للقانون $" \times "$ هو $M (\frac{- x}{1 + x})$ فإن $(E, T, \times)$ جسم تبادلي
4

التمرين 4

التحليل

الجزء الأول

لتكن $f$ الدالة العددية المعرفة على المجال $[0, + \infty [$ بما يلي

$\{\begin{cases} f (0) = 0 \\ (x > 0) f (x) = x (1 + \ln^{2} x) \end{cases}$

ليكن $(C)$ المنحنى الممثل للدالة $f$ في المستوى المنسوب إلى معلم متعامد ممنظم $(O, \vec{i}, \vec{j})$

$1$ احسب $\lim_{x \to + \infty} f (x)$ و $\lim_{x \to + \infty} \frac{f (x)}{x}$ ثم أول مبيانيا النتيجة المحصل عليها

$2$

$أ$ بين أن الدالة $f$ متصلة على اليمين في $0$

$ب$ احسب $\lim_{x \to 0^{+}} \frac{f (x)}{x}$ ثم أول مبيانيا النتيجة المحصل عليها

$ج$ احسب $f' (x)$ من أجل $x > 0$ ثم استنتج أن الدالة $f$ تزايدية قطعا على المجال $[0, + \infty [$

$3$

$أ$ بين أن المنحنى $(C)$ يقبل نقطة انعطاف $I$ أفصولها $e^{- 1}$

$ب$ أدرس الوضع النسبي للمنحنى $(C)$ بالنسبة للمستقيم الذي معادلته $y = x$

$ج$ أنشئ المنحنى $(C)$ (نأخد $e^{- 1} = 0, 4$ )

الجزء الثاني

نعتبر المتتالية العددية ${(u_{n})}_{n \geq 0}$ المعرفة بما يلي

$\{\begin{cases} u_{0} = e^{- 1} \\ (\forall n \in ℕ) u_{n + 1} = f (u_{n}) \end{cases}$

$1$ بين بالترجع أن $(\forall n \in ℕ) e^{- 1} \leq u_{n} < 1$

$2$ بين أن المتتالية ${(u_{n})}_{n \geq 0}$ تزايدية قطعا ثم استنتج أنها متقاربة

$3$ نضع $\lim_{n \to + \infty} u_{n} = l$

$أ$ بين أن $(\forall n \in ℕ) e^{- 1} \leq l \leq 1$

$ب$ حدد قيمة $l$

الجزء الثالث

لتكن $F$ الدالة المعرفة على المجال $[0, + \infty [$ بما يلي $F (x) = \int_{1}^{x} f (t) d t$

$1$

$أ$ بين أن الدالة $H : x \to \frac{1}{4} x^{2} + \frac{1}{2} x^{2} \ln x$ دالة أصلية للدالة $h : x \to x \ln$ على المجال $[0, + \infty [$

$ب$ بين أن $(\forall x > 0) \int_{1}^{x} t \ln^{2} (t) d t = \frac{x^{2}}{2} \ln^{2} (x) - \int_{1}^{x} t \ln (t) d t$

$ج$ استنتج أن $(\forall x > 0) F (x) = - \frac{3}{4} + \frac{3 x^{2}}{4} - \frac{x^{2}}{2} \ln (x) + \frac{x^{2}}{2} \ln^{2} (x)$

$2$

$أ$ بين أن الدالة $F$ متصلة على المجال $[0, + \infty [$

$ب$ احسب $\lim_{x \to 0^{+}} F (x)$ ثم استنتج قيمة التكامل $\int_{0}^{1} f (x) d x$

التحليل

الجزء الأول

$1$ لدينا

$\lim_{x \to + \infty} f (x) = \lim_{x \to + \infty} x (1 + \ln^{2} x) = + \infty$

و

$\lim_{x \to + \infty} \frac{f (x)}{x} = \lim_{x \to + \infty} (1 + \ln^{2} x) = + \infty$

إذن $(C)$ يقبل فرعا شلجميا في اتجاه محور الأراتيب بجوار $+ \infty$

$2$

$أ$ لدينا $f (0) = 0$ و

$\lim_{x \to 0^{+}} f (x) = \lim_{x \to 0^{+}} x (1 + \ln^{2} x) \lim_{x \to 0^{+}} f (x) = \lim_{x \to 0^{+}} x + 4 {(\sqrt{x} \ln \sqrt{x})}^{2} \lim_{x \to 0^{+}} f (x) = 0$

ومنه $f$ متصلة على اليمين في $0$

$ب$ لدينا $\lim_{x \to 0^{+}} \frac{f (x)}{x} = \lim_{x \to 0^{+}} (1 + \ln^{2} x) = + \infty$

إذن $f$ غير قابلة للاشتقاق على اليمين في $0$ ، هندسيا $(C)$ يقبل نصف مماس عمودي موجه نحو الأعلى على يمين النقطة $O (0, 0)$

$ج$ لدينا $f$ قابلة للاشتقاق على $[0, + \infty [$ كجداء ومجموع دوال قابلة للاشتقاق على المجال $[0, + \infty [$

ولدينا

$f' (x) = (1 + \ln^{2} x) + x (2 \frac{1}{x} \ln x) f' (x) = 1 + \ln^{2} x + \ln x f' (x) = = {(1 + \ln x)}^{2}$

بما أن $(\forall x \in [0, + \infty [) f' (x) \geq 0$

فإن $f$ تزايدية قطعا على $[0, + \infty [$

$3$

$أ$ لدينا $f' (x) = {(1 + \ln x)}^{2}$ و $f' (x) = 0 \Leftrightarrow x = e^{- 1}$

إذن $f'$ تنعدم في $e^{- 1}$ ولا تغير إشارتها على يمين وعلى يسار $e^{- 1}$

ومنه $(C)$ يقبل نقطة انعطاف أفصولها $e^{- 1}$

$ب$ لدينا

$\forall x > 0; f (x) - x = x (1 + \ln^{2} x - 1) = x \ln^{2} x \geq 0$

إذن $(C)$ يوجد فوق $(Δ) y = x$ ويقطعه في النقطتين $O (0, 0)$ و $A (1, 0)$

$ج$ إنشاء $(C)$

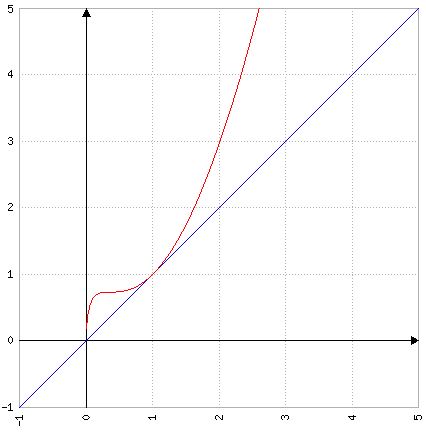
الجزء الثاني

$1$ لدينا $e^{- 1} \leq u_{0} = e^{- 1} < 1$

نفترض أن $e^{- 1} \leq u_{n} < 1$ ولنبين أن $e^{- 1} \leq u_{n + 1} < 1$

لدينا $e^{- 1} \leq u_{n} < 1$ و $f$ دالة تزايدية قطعا على $[0, + \infty [$

إذن $f (e^{- 1}) \leq f (u_{n}) < f (1)$

وبما أن $f (1) = 1$ و $f (e^{- 1}) = 2 e^{- 1} \geq e^{- 1}$

فإن $e^{- 1} \leq 2 e^{- 1} \leq u_{n + 1} < 1$

ومنه

$(\forall n \in ℕ) e^{- 1} \leq u_{n} < 1$

$2$ لدينا

$(\forall n \in ℕ) u_{n + 1} - u_{n} = u_{n} \ln^{2} (u_{n}) > 0$

ومنه ${(u_{n})}_{n \geq 0}$ متتالية تزايدية قطعا، وبما أنها مكبورة بالعدد $1$ فهي متقاربة

$3$

$أ$ نعلم أن $(\forall n \in ℕ) e^{- 1} \leq u_{n} \leq 1$

إذن

$e^{- 1} \leq \lim_{n \to + \infty} u_{n} \leq 1 \Rightarrow e^{- 1} \leq l \leq 1$

$ب$ لدينا $f$ متصلة على $[e^{- 1}, 1]$

و $f ([e^{- 1}, 1]) = [2 e^{- 1}, 1] \subset [e^{- 1}, 1]$ و ${(u_{n})}_{n \geq 0}$ متقاربة نهايتها $l$

إذن $l$ حل المعادلة $f (x) = x$ والتي حسب الجزء الأول تقبل حلين $1$ و $0$

وبما أن $e^{- 1} \leq l \leq 1$ فإن

$l = 1$

الجزء الثالث

$1$

$أ$ لدينا لكل $x > 0$

$H' (x) = {(- \frac{1}{4} x^{2} + \frac{1}{2} x^{2} \ln x)}^{'} H' (x) = \frac{- 2}{4} x + \frac{1}{2} (2 x \ln x + x^{2} \times \frac{1}{x}) H' (x) = \frac{- 1}{2} + x \ln x + \frac{1}{2} x H' (x) = x \ln x H' (x) = h (x)$

إذن الدالة $H$ هي دالة أصلية للدالة $h$

$ب$ لدينا لكل $x > 0$

$A = \int_{1}^{x} t \ln^{2} (t) d t A = \int_{1}^{x} {(\frac{1}{2} t^{2})}^{'} \ln^{2} (t) d t A = {[\frac{1}{2} t^{2} \ln^{2} (t)]}_{1}^{x} - \int_{1}^{x} \frac{1}{2} t^{2} \times 2 \ln (t) \times \frac{1}{t} d t A = \frac{x^{2}}{2} \ln^{2} (x) - \int_{1}^{x} t \ln (t) d t$

$ج$ لدينا لكل $x > 0$

$F (x) = \int_{1}^{x} t (1 + \ln^{2} (t)) d t F (x) = \int_{1}^{x} t + t \ln^{2} (t) d t F (x) = \int_{1}^{x} t d t + \int_{1}^{x} t \ln^{2} (t) d t F (x) = {[\frac{1}{2} t^{2}]}_{1}^{x} + \frac{x^{2}}{2} \ln^{2} (x) - {[\frac{- 1}{4} t^{2} + \frac{1}{2} t^{2} \ln t]}_{1}^{x} F (x) = \frac{x^{2}}{2} - \frac{1}{2} + \frac{x^{2}}{2} \ln^{2} (x) - (\frac{- x^{2}}{4} + \frac{x^{2}}{2} \ln x) + (\frac{- 1}{4}) F (x) = \frac{x^{2}}{2} - \frac{1}{2} + \frac{x^{2}}{2} \ln^{2} (x) + \frac{x^{2}}{4} - \frac{x^{2}}{2} \ln (x) - \frac{1}{4} F (x) = - \frac{3}{4} + \frac{3 x^{2}}{4} - \frac{x^{2}}{2} \ln (x) + \frac{x^{2}}{2} \ln^{2} (x)$

$2$

$أ$ الدالة $f$ متصلة على $[0, + \infty [$

إذن فهي تقبل دالة أصلية $k$ متصلة وقابلة للاشتقاق على $[0, + \infty [$

ومنه $\forall x \in [0, + \infty [; F (x) = k (x) - k (1)$

مما يعني أن الدالة $F$ متصلة علي $[0, + \infty [$

$ب$

$A = \lim_{x \to 0^{+}} F (x) A = \lim_{x \to 0^{+}} - \frac{3}{4} + \frac{3 x^{2}}{4} - \frac{x^{2}}{2} \ln (x) + \frac{x^{2}}{2} \ln^{2} (x) A = - \frac{3}{4} \lim_{x \to 0^{+}} F (x) = - \frac{3}{4}$

بما أن $F$ متصلة على $[0, + \infty [$ فإن $F$ متصلة على اليمين في $0$

ومنه $\lim_{x \to 0^{+}} F (x) = F (0) = - \frac{3}{4}$

$\int_{0}^{1} f (x) d x = - \frac{3}{4}$
5

التمرين 5

التحليل 2

نعتبر الدالة $g$ المعرفة على المجال $[0, + \infty [$ بما يلي

$\{\begin{cases} g (0) = \ln 2 \\ g (x) = \int_{x}^{2 x} \frac{e^{- t}}{t} d t (x > 0) \end{cases}$

$1$

$أ$ بين أن $(\forall x > 0) (\forall t \in [x, 2 x]) e^{- 2 x} \leq e^{- t} \leq e^{- x}$

$ب$ بين أن $(\forall x > 0) e^{- 2 x} \ln 2 \leq g (x) \leq e^{- x} \ln 2$

$ج$ استنتج أن الدالة $g$ متصلة على اليمين في $0$

$2$ بين أن الدالة $g$ قابلة للاشتقاق على المجال $] 0, + \infty [$ ثم احسب $g' (x)$ من أجل $x > 0$

$3$

$أ$ بين أن $(\forall t > 0) - 1 \leq \frac{e^{- t} - 1}{t} \leq - e^{- t}$ (يمكنك استعمال مبرهنة التزايدات المنتهية)

$ب$ بين أن $(\forall x > 0) - 1 \leq \frac{g (x) - \ln 2}{x} \leq \frac{e^{- 2 x} - e^{- x}}{x}$

$ج$ استنتج أن الدالة $g$ قابلة للاشتقاق على اليمين في $0$

التحليل 2

$1$

$أ$ ليكن $x > 0$

لدينا

$t \in [x, 2 x] \Rightarrow x \leq t \leq 2 x \Rightarrow - 2 x \leq - t \leq - x \Rightarrow e^{- 2 x} \leq e^{- t} \leq e^{- x}$

$ب$ ليكن $x > 0$

حسب السؤال السابق نستنتج أن

$(\forall t \in [x, 2 x]) \frac{e^{- 2 x}}{t} \leq \frac{e^{- t}}{t} \leq \frac{e^{- x}}{t} \Rightarrow \int_{x}^{2 x} \frac{e^{- 2 x}}{t} d t \leq \int_{x}^{2 x} \frac{e^{- t}}{t} d t \leq \int_{x}^{2 x} \frac{e^{- x}}{t} d t \Rightarrow e^{- 2 x} \int_{x}^{2 x} \frac{1}{t} d t \leq g (x) \leq e^{- x} \int_{x}^{2 x} \frac{1}{t} d t \Rightarrow e^{- 2 x} {[\ln t]}_{x}^{2 x} \leq g (x) \leq e^{- x} {[\ln t]}_{x}^{2 x} \Rightarrow e^{- 2 x} \ln 2 \leq g (x) \leq e^{- x} \ln 2$

إذن $(\forall x > 0) e^{- 2 x} \ln 2 \leq g (x) \leq e^{- x} \ln 2$

$ج$ بما أن $\lim_{x \to 0^{+}} e^{- x} \ln 2 = \ln 2$ و $\lim_{x \to 0^{+}} e^{- 2 x} \ln 2 = \ln 2$

فإن $\lim_{x \to 0^{+}} g (x) = \ln 2 = g (0)$

إذن الدالة $g$ متصلة على اليمين في $0$

$2$ بين أن الدالة $g$ قابلة للاشتقاق على المجال $] 0, + \infty [$ ثم احسب $g' (x)$ من أجل $x > 0$

بما أن الدالة $t \mapsto \frac{e^{- t}}{t}$ متصلة على $] 0, + \infty [$ فهي تقبل دالة أصلية $G$ متصلة وقابلة للاشتقاق على هذا المجال

لدينا $(\forall x > 0) g (x) = G (2 x) - G (x)$

وبما أن $x \mapsto 2 x$ قابلة للاشتقاق على $] 0, + \infty [$ فإن الدالة $g$ قابلة للاشتقاق على $] 0, + \infty [$

ولدينا

$(\forall x > 0) g' (x) = 2 G' (2 x) - G' (x) (\forall x > 0) g' (x) = 2 \frac{e^{- 2 x}}{2 x} - \frac{e^{- x}}{x} (\forall x > 0) g' (x) = \frac{e^{- 2 x} - e^{- x}}{x}$

$3$

$أ$ ليكن $t > 0$

الدالة $p : x \mapsto e^{- x}$ متصلة على $[0, t]$ وقابلة للاشتقاق على $] 0, t [$ ، إذن حسب مبرهنة التزايدات المنتهية:

$\exists c_{t} \in] 0, t [; \frac{p (t) - p (0)}{t} = p' (c_{t}) \Rightarrow \exists c_{t} \in] 0, t [; \frac{e^{- t} - 1}{t} = - e^{- c_{t}}$

ولدينا

$c_{t} \in] 0, t [\Rightarrow 0 < c_{t} < t \Rightarrow - t < - c_{t} < 0 \Rightarrow e^{- t} < e^{- c_{t}} < 1 \Rightarrow - 1 < - e^{- c_{t}} < - e^{- t}$

إذن

$(\forall t > 0) - 1 \leq \frac{e^{- t} - 1}{t} \leq - e^{- t}$

$ب$ لدينا

$(\forall t > 0) - 1 \leq \frac{e^{- t} - 1}{t} \leq - e^{- t} \Rightarrow (\forall x > 0) \int_{x}^{2 x} - 1 d t \leq \int_{x}^{2 x} \frac{e^{- t} - 1}{t} d t \leq \int_{x}^{2 x} - e^{- t} d t \Rightarrow (\forall x > 0) {[- t]}_{x}^{2 x} \leq \int_{x}^{2 x} \frac{e^{- t}}{t} d t - \int_{x}^{2 x} \frac{1}{t} d t \leq {[e^{- t}]}_{x}^{2 x} \Rightarrow (\forall x > 0) - 2 x + x \leq g (x) - \ln 2 \leq e^{- 2 x} - e^{- x} \Rightarrow (\forall x > 0) - 1 \leq \frac{g (x) - \ln 2}{x} \leq \frac{e^{- 2 x} - e^{- x}}{x}$

$ج$ لدينا

$A = \lim_{x \to 0^{+}} \frac{e^{- 2 x} - e^{- x}}{x} A = \lim_{x \to 0^{+}} \frac{e^{- 2 x} - 1}{x} - \frac{e^{- x} - 1}{x} A = \lim_{x \to 0^{+}} - 2 \frac{e^{- 2 x} - 1}{- 2 x} + \frac{e^{- x} - 1}{- x} A = - 2 \times 1 = - 1$

إذن $\lim_{x \to 0^{+}} \frac{g (x) - \ln 2}{x} = - 1$ أي $\lim_{x \to 0^{+}} \frac{g (x) - g (0)}{x} = - 1$

ومنه $g$ قابلة للاشتقاق على اليمين في $0$

Retour

الامتحان الوطني الموحد 2015 الدورة العادية: الموضوع والتصحيح

التمرين 1

الأعداد العقدية

الأعداد العقدية

التمرين 2

الحسابيات

الحسابيات

التمرين 3

البنيات الجبرية

البنيات الجبرية

التمرين 4

التحليل

الجزء الأول

الجزء الثاني

الجزء الثالث

التحليل

الجزء الأول

الجزء الثاني

الجزء الثالث

التمرين 5

التحليل 2

التحليل 2

Maroc

France

Plus