الامتحان الوطني الموحد 2015 الدورة الإستدراكية: الموضوع والتصحيح

الكيمياء

الجزء الأول: دراسة محلول مائي لحمض الإيثانويك وتصنيع إستر

$\boxed{1}$ دراسة محلول مائي لحمض الإيثانويك

$\boxed{1-1}$ معادلة تفاعل حمض الإيثانويك مع الماء:

$\boxed{{\mathrm{CH}}_3{\mathrm{COOH}}_{\left(\mathrm{aq}\right)}+{\mathrm{H}}_2{\mathrm{O}}_{\left(\mathrm{l}\right)}\rightleftarrows {\mathrm{CH}}_3{{\mathrm{COOH}}^{-}}_{\left(\mathrm{aq}\right)}+{\mathrm{H}}_3{\mathrm{O}}_{\left(\mathrm{aq}\right)}^{+}}$

$\boxed{2-1}$ إثبات قيمة $\mathrm{PH}$:

الجدول الوصفي لتقدم التفاعل:

حسب تعريف الموصلية:

$\mathrm{\sigma }={\mathrm{\lambda }}_{\left({\mathrm{CH}}_3{\mathrm{COO}}^{-}\right)}{\left[{\mathrm{CH}}_3{\mathrm{COO}}^{-}\right]}_{\mathrm{éq}}+{\mathrm{\lambda }}_{{\mathrm{H}}_3\mathrm{O}}+{\left[{\mathrm{H}}_3{\mathrm{O}}^{+}\right]}_{\mathrm{éq}}$

حسب الجدول الوصفي:

$$\begin{gathered} {\left[({\mathrm{C}}^{-}{\mathrm{H}}_3\mathrm{COO}\right]}_{\mathrm{éq}}={\left[{\mathrm{H}}_3{\mathrm{O}}^{+}\right]}_{\mathrm{éq}}=\frac{{\mathrm{x}}_{\mathrm{éq}}}{{\mathrm{V}}_{\mathrm{A}}} \\ \Rightarrow {\mathrm{\sigma }=\mathrm{\lambda }({\mathrm{CH}}_3\mathrm{COO}}^{-}){\left[{\mathrm{H}}_3{\mathrm{O}}^{+}\right]}_{\mathrm{éq}}+{\mathrm{\lambda }}_{\left({\mathrm{H}}_3{\mathrm{O}}^{+}\right)}{\left[{\mathrm{H}}_3{\mathrm{O}}^{+}\right]}_{\mathrm{éq}} \end{gathered}$$

تعبير $\mathrm{PH}$:

لدينا:

$$\begin{gathered} \mathrm{pH}=-\log {\left[{\mathrm{H}}_3{\mathrm{O}}^{+}\right]}_{\mathrm{éq}} \\ \mathrm{pH}=-\log \left(\frac{\mathrm{\sigma }}{{\mathrm{\lambda }}_{\left({\mathrm{CH}}_3{\mathrm{COO}}^{-}\right)}+{\mathrm{\lambda }}_{\left({\mathrm{H}}_3{\mathrm{O}}^{+}\right)}}\right) \end{gathered}$$

ت.ع:

$$\begin{gathered} \mathrm{pH}=-\log \left(\frac{1,6.{10}^{-2}}{3,49.{10}^{-2}+4,09.{10}^{-3}}\times {10}^{-3}\right) \\ \boxed{pH\simeq 3,4} \end{gathered}$$

$\boxed{3-1}$ حساب نسبة التقدم النهائي:

تعبير نسبة التقدم النهائي:

$$\begin{gathered} \tau =\frac{x_{éq}}{x_{max}} \\ \tau =\frac{{\left[H_3{O}^{+}\right]}_{éq}.V}{C_A.V} \\ \tau =\frac{{\left[H_3{O}^{+}\right]}_{éq}}{C_A} \\ \tau =\frac{{10}^{-pH}}{C_A} \end{gathered}$$

ت.ع:

$\boxed{\tau =\frac{{10}^{-3,4}}{{10}^{-2}}=0,04=4\%}$

$\boxed{4-1}$ تعبير $p{K}_A$ بدلالة $pH$ و$C_A$:

حسب تعريف ثابتة الحمضية:

$K_A=\frac{{\left[C{H}_{3}CO{O}^{-}\right]}_{éq}{\left[H_3{O}^{+}\right]}_{éq}}{{\left[C{H}_{3}COOH\right]}_{éq}}$

حسب الجدول الوصفي:

$$\begin{gathered} \left\{\begin{array}{l}{\left[C{H}_{3}CO{O}^{-}\right]}_{éq}={\left[H_3{O}^{+}\right]}_{éq}=\frac{x_{éq}}{V}\\ {\left[C{H}_{3}COOH\right]}_{éq}=\frac{C_A.V_A-x_{éq}}{V_A}=C_A-\frac{x_{éq}}{V_A}\end{array}\right. \\ \Rightarrow \left\{\begin{array}{l}{\left[C{H}_{3}CO{O}^{-}\right]}_{éq}={\left[H_3{O}^{+}\right]}_{éq}={10}^{-pH}\\ {\left[C{H}_{3}COOH\right]}_{éq}=C_A-{10}^{-pH}\end{array}\right. \end{gathered}$$

$K_A=\frac{{\left({10}^{-pH}\right)}^2}{C_A-{10}^{-pH}}=\frac{{10}^{-2pH}}{C_A-{10}^{-pH}}$

لدينا: $p{K}_A=-\log K_A$

أي:

  $$\begin{gathered} p{K}_A=-\log \left(\frac{{10}^{-2pH}}{C_A-{10}^{-pH}}\right) \\ p{K}_A=-\log \left(\frac{{10}^{-2\times 3,4}}{{10}^{-2}-{10}^{-3,4}}\right) \\ \boxed{p{K}_A\simeq 4,8} \end{gathered}$$

$\boxed{2}$ تصنيع الإستر

$\boxed{1-2}$ يلعب حمض الكبريتيك دور الحفاز هدفه تسريع التفاعل

دور الماء المثلج هو توقيف التفاعل

$\boxed{2-2}$ معادلة التفاعل بين حمض الإيثانويك ومحلول هيدروكسيد الصوديوم:

$\boxed{C{H}_{3}COO{H}_{\left(aq\right)}+H{O}_{\left(aq\right)}^{-}\rightleftarrows C{H}_{3}CO{O}_{\left(aq\right)}^{-}+H_2{O}_{\left(l\right)}}$

$\boxed{3-2}$ اختيار الجواب الصحيح:

$\boxed{ب}$ عند درجة حرارة معينة تتناقص سرعة تفاعل الأسترة مع مرور الزمن

$\boxed{4-2}$ معادلة تفاعل الاسترة:

$\boxed{C{H}_3-COOH+R-OH\rightleftarrows C{H}_3-COO-R+H_{2}O}$

$\boxed{5-2}$ تحديد قيمة السرعة الحجمية للتفاعل عند اللحظة $t=0$:

لدينا:   $v\left(t\right)=\frac{1}{V}.\frac{dx}{dt}$

كمية الحمض المتبقي: $n_r=0,2-x$ 

ومنه: $\frac{d{n}_r}{dt}=-\frac{dx}{dt}$  أي:   $\frac{dx}{dt}=-\frac{d{n}_r}{dt}$

$v\left(t\right)=\frac{1}{V}.\frac{dx}{dt}=-\frac{1}{V}.\frac{d{n}_r}{dt}$

عند $t=0$ نكتب: $v\left(0\right)=-\frac{1}{V}{\left(\frac{\Delta n_r}{\Delta t}\right)}_{t=0}$

مبيانيا:

$$\begin{gathered} v\left(0\right)=-\frac{1}{46.{10}^{-3}}\times \frac{\left(0,2-0,14\right)}{\left(0-30\right)} \\ \boxed{v\left(0\right)\simeq 4,35.{10}^{-2} mol.L^{-1}.mi{n}^{-1}} \end{gathered}$$

$\boxed{6-2}$ تحديد $t_{1/2}$  قيمة زمن نصف التفاعل:

عند اللحظة: $t_{1/2}$   يكون:  $x\left(t{ }_{1/2}\right)=\frac{x_f}{2}$

نعلم أن:  $n_{r f}=0,2-x_f$  أي:  $x_f=0,2-n_{r f}$

عند اللحظة  $t_{1/2}$  لدينا:  

$$\begin{gathered} x\left(t_{1/2}\right)=\frac{x_f}{2} \\ x\left(t_{1/2}\right)=\frac{0,2-n_{r f}}{2} \\ x\left(t_{1/2}\right)=0,1-\frac{n_{r f}}{2} \end{gathered}$$

مبيانيا:  $n_{r f}=0,08 mol$

ومنه:  $x\left(t_{1/2}\right)=0,1-\frac{0,08}{2}=0,06 mol$

نحدد  $n_r\left(t_{1/2}\right)$  حيث:  $n_r\left(t_{1/2}\right)=0,2-x\left(t_{1/2}\right)=0,2-0,06=0,14mol$

مبيانيا نجد عند $n_r\left(t_{1/2}\right)=0,14 mol$  زمن نصف التفاعل هو

$\boxed{t_{1/2}=42 min}$

$\boxed{7-2}$ حساب مردود تفاعل الأسترة:

$r=\frac{n_{exp}\left(ester\right)}{n_{max}\left(ester\right)}$

عند نهاية التفاعل كمية مادة الاستر المحصل عليها هي $x_f=0,2-n_{r f}$

أي $x_f=0,2-0,08=0,12 mol$

وبالتالي

$\boxed{r=\frac{x_f}{x_{max}}=\frac{0,12}{0,2}=60\%}$

$\boxed{8-2}$ تحديد كمية مادة الاستر المتكون والحمض المتبقي:

الجدول الوصفي للتجربة الأولى لحساب ثابتة التوازن $K$:

ثابتة التوازن

$$\begin{gathered} K=\frac{{\left[acide\right]}_{éq}{\left[alcool\right]}_{éq}}{{\left[ester\right]}_{éq}{\left[H_{2}O\right]}_{éq}} \\ K=\frac{{\left({\displaystyle \frac{x_{éq}}{V}}\right)}^2}{{\left({\displaystyle \frac{0,2-x_{éq}}{V}}\right)}^2} \\ K=\frac{x_{éq}^2}{{\left(0,2-x_{éq}\right)}^2} \end{gathered}$$

ت ع:

$K=\frac{{\left(0,12\right)}^2}{{\left(0,2-0,12\right)}^2}=2,25$

الجدول الوصفي للتجربة الثانية لحساب  $x{\text{'}}_{éq}$

ثابتة التوازن تكتب:

$$\begin{gathered} K=\frac{{\left[acide\right]}_{éq}{\left[alcool\right]}_{éq}}{{\left[ester\right]}_{éq}{\left[H_{2}O\right]}_{éq}} \\ K=\frac{{\left({\displaystyle \frac{x{\text{'}}_{éq}}{V}}\right)}^2}{\left({\displaystyle \frac{0,3-x{\text{'}}_{éq}}{V}}\right).\left({\displaystyle \frac{0,2-x{\text{'}}_{éq}}{V}}\right)} \\ K=\frac{x{\text{'}}_{éq}^2}{\left(0,3-x{\text{'}}_{éq}\right).\left(0,2-x{\text{'}}_{éq}\right)} \end{gathered}$$

 $K\left(0,3-x{\text{'}}_{éq}\right).\left(0,2-x{\text{'}}_{éq}\right)=x{\text{'}}_{éq}^2$

أي $x{\text{'}}_{éq}^2\left(K-1\right)-0,5.K.x{\text{'}}_{éq}+0,06.K=0$  مع $K=2,25$

إذن $1,25.x{\text{'}}_{éq}-1,125x{\text{'}}_{éq}+0,135=0$

$x{\text{'}}_{éq}=\frac{1,125\mp \sqrt{1,{125}^2-4\times 1,25\times 0,135}}{2\times 1,25}$

أي:   $x{\text{'}}_{éq 1}=0,757 mol$    أو     $x{\text{'}}_{éq 2}=0,142 mol$

بما أن:  $x{\text{'}}_{éq}<0,2 mol$    فإن: التقدم النهائي هو :  $x{\text{'}}_{éq }=0,142 mol$

كمية مادة الإستر المتكونة هي:  $n_f\left(ester\right)=x{\text{'}}_{éq}=0,142 mol$

كمية مادة الحمض المتبقية هي: $x_f\left(acide\right)=0,3-x{\text{'}}_{éq}=0,158 mol$

الجزء الثاني: التحضير الصناعي لغاز ثنائي الكلور

$\boxed{1}$ كتابة معادلة التفاعل عند الكاثود

يحدث عند الكاثود اختزال كاثودي للمؤكسد $H_{2}O$ وفق المعادلة التالية:

$H_2{O}_{\left(l\right)}+2e^{-}\rightleftarrows H_{2\left(g\right)}+H{O}_{\left(aq\right)}^{-}$

بجوار هذا الكاثود تتكون أيونات $H{O}^{-}$ وبالتالي يكون الوسط قاعديا أي  $pH>7$

$\boxed{2}$ إيجاد حجم غاز $C{l}_2$  الناتج خلال المدة $∆t$

حسب الأكسدة الأنودية:  $2C{l}_{\left(aq\right)}^{-}\rightleftarrows C{l}_{2\left(g\right)}+2e^{-}$

لدينا:  $n\left(C{l}_2\right)=\frac{n\left(e^{-}\right)}{2}$

مع:

$\left\{\begin{array}{l}n\left(C{l}_2\right)=\frac{v\left(C{l}_2\right)}{v_m}\\ n\left(e^{-}\right)=\frac{Q}{F}=\frac{I.∆t}{F}\end{array}\right.$ 

أي: $\frac{V\left(C{l}_2\right)}{V_m}=\frac{I.∆t}{2F}$ 

وبالتالي:

$\boxed{V\left(C{l}_2\right)=\frac{I.∆t}{2F}.V_m}$

ت.ع:

$$\begin{gathered} V\left(C{l}_2\right)=\frac{50.{10}^3\times 10\times 3600\times 24}{2\times 9,65.{10}^4} \\ V\left(C{l}_2\right)=223,83.{10}^{3}l \\ \boxed{V\left(C{l}_2\right)=223,83 m^3} \end{gathered}$$

الموجات الضوئية

$\boxed{1}$ اختيار الجواب الصحيح من بين الاقتراحات

$\boxed{د}$ يتعلق معامل انكسار وسط شفاف بطول الموجة للضوء الأحادي اللون الذي يجتازه
تعليل: حسب تعبير معامل الانكسار: $n=\frac{{\lambda }_0}{\lambda }$  حيث: $\lambda$ : طول موجة الضوء في الوسط الشفاف و ${\lambda }_0$ : طول موجته في الفراغ

$\boxed{2}$ تحديد $∆E$ تغير الطاقة بـ $MeV$

لدينا:  $∆E=hv=\frac{h.c}{{\lambda }_0}$ 

ت.ع:

$$\begin{gathered} ∆E=\frac{6,63.{10}^{-34}\times 3.{10}^8}{633.{10}^{-9}} \\ ∆E=3,142 J \\ \boxed{∆E=1,96.{10}^{-6} MeV} \end{gathered}$$

$\boxed{3}$

$\boxed{1-3}$ نعم ينتمي هذا الإشعاع الى مجال الطيف المرئي لأن: 

$400 nm<{\lambda }_0=633 nm<800 nm$

$\boxed{2-3}$ حساب تردد الإشعاع:

$c={\lambda }_0.v$ ومنه: $v=\frac{c}{{\lambda }_0}$

ت.ع: 

$\boxed{v=\frac{3.{10}^8}{633.{10}^{-9}}=4,74.{10}^{14 }Hz}$

$\boxed{3-3}$ تحديد سرعة الانتشار $v$  وطول الموجة $\lambda$  للإشعاع في الموشور:

لدينا: $n=\frac{c}{v}$  ومنه: $v=\frac{c}{n}$ 

ت.ع:   $v=\frac{.3.{10}^8}{1,61}=1,86.{10}^8 m.s^{-1}$
لدينا: $n=\frac{{\lambda }_0}{\lambda }$  ومنه: $\lambda =\frac{{\lambda }_0}{n}$ 

ت.ع:

$\boxed{\lambda =\frac{633}{1,61}=393,16 nm}$

$\boxed{4-3}$ نلاحظ بقعة ضوئية تمتد ألوانها من الأحمر الى البنفسجي تسمى طيف الضوء الأبيض

تبرز هذه التجربة ظاهرة تبدد الضوء الأبيض بواسطة موشور

الكهرباء

$\boxed{I}$ دراسة ثنائي القطب $RC$ والدارة المثالية $LC$

$\boxed{1}$ دراسة ثنائي القطب $RC$

$\boxed{1-1}$ المنحنى الممثل للتوتر $u_c\left(t\right)$

بما أن المكثف غير مشحون بدئيا فإنه عند $t=0$  يكون: $u_c\left(0\right)=0$  أي المنحنى يمر من أصل المعلم ومنه فإن المنحنى الذي يمثل التوتر $u_c\left(t\right)$ هو ${\Gamma }_1$

$\boxed{2-1}$ المعادلة التفاضلية التي يحققها التوتر $u_c\left(t\right)$

حسب قانون إضافية التوترات: $u_R+u_r+u_c=E$

حسب قانون أوم:  $Ri+ri+u_c=E \left(1\right)$

مع: $i=\frac{dq}{dt}=\frac{d\left(c_0.u_c\right)}{dt}=C_0.\frac{d{u}_c}{dt}$ 

نعوض في المعادلة $\left(1\right)$ ونحصل على المعادلة التفاضلية:

$\boxed{\left(R+r\right).C_0.\frac{d{u}_c}{dt}+u_c=E}$

$\boxed{3-1}$ إثبات تعبير شدة التيار  $i_0$

عند اللحظة $t=0$  لدينا $u_c\left(0\right)=0$ و $i\left(0\right)=i_0$ 

نعوض في المعادلة $\left(1\right)$ فنحصل على $\left(R+r\right).i_0=E$ 

ومنه:

$\boxed{i_0=\frac{E}{R+r}}$

$\boxed{4-1}$

$\boxed{1-4-1}$ تحديد قيمة  $r$

في النظام الدائم لدينا: $E=6V$

عند اللحظة $t=0$  حسب المنحنى ${\Gamma }_2$ لدينا $u_{r_0}=4V$  مع $u_{r_0}=E-r.i_0$ 

ومنه: $i_0=\frac{E-u_{r_0}}{r}$

حسب التعبير $i_0=\frac{E}{R+r}$  نحصل على: $\frac{E-u_{r_0}}{r}=\frac{E}{R+r}$

أي $\left(R+r\right).\left(E-u_{r_0}\right)=r.E$

ومنه:  $r.\left(E-u_{r_0}\right)-r.E=-R.\left(E-u_{r_c}\right)$ 

أي: $r=\frac{R.\left(E-u_{r_0}\right)}{u_{r_0}}$

ت.ع:

$\boxed{r=\frac{20\times \left(6-4\right)}{4}=10\Omega }$

$\boxed{2-4-1}$ إثبات قيمة $C_0$

باستعمال الشكل $2$  قيمة ثابتة الزمن $\tau$ هي: $\tau =0,15 ms=1,5.{10}^{-4} s$

لدينا: $\tau =\left(R+r\right).c_0$  أي: $c_0=\frac{\tau }{R+r}$ 

ت.ع:

$\boxed{c_0=\frac{1,5.{10}^{-4}}{20+10}=5 \mu F}$

$\boxed{2}$ الدارة المثالية  $LC$

$\boxed{1-2}$ إثبات المعادلة التفاضلية التي تحققها شدة التيار $i\left(t\right)$

تطبيق قانون إضافية التوترات: $u_L+u_c=0 \left(1\right)$

قانون أوم: $u_L=L_0.\frac{di}{dt}$
لدينا: $q=C.u_c$  و $i=\frac{dq}{dt}=\frac{d\left(C_0{u}_c\right)}{dt}=C_0.\frac{d{u}_c}{dt}$

المعادلة $\left(1\right)$  تكتب:  $L_0.\frac{di}{dt}+\frac{q}{C_0}=0$

ومنه:  $L_0.C_0.\frac{di}{dt}+q=0$

إذن $L_0.C_0.\frac{d}{dt}\left(\frac{di}{dt}\right)+\frac{dq}{dt}=0$

المعادلة التفاضلية:

$\boxed{L_0.C_0.\frac{d^{2}i}{d{t}^2}+i=0}$

$\boxed{2-2}$ إيجاد قيمة $\phi$:

حل المعادلة التفاضلية يكتب:  $i\left(t\right)=I_m\cos \left(\frac{2\pi }{T_0}.t+\phi \right)$

حسب الشروط البدئية لدينا:  $i\left(0\right)=0$

حل المعادلة التفاضلية يكتب:  $i\left(0\right)=I_m\cos \phi =0$  أي:  $\phi =\pm \frac{\pi }{2}$

عند اللحظة $t=0$  لدينا: $u_c\left(0\right)=E>0$   مع  $i=C_0.\frac{d{u}_c}{dt}$ 

أي: 

$u_c=\frac{1}{C_0}\int idt=\frac{T_0}{2\mathrm{\pi }}.\frac{1}{C_0}{I}_m.\sin \left(\frac{2\mathrm{\pi }}{T_0}.t+\phi \right)$

$u_c\left(0\right)=\frac{T_0}{2\mathrm{\pi }}.\frac{I_m}{C_0}.\sin \phi >0$ 

الخلاصة:

$\boxed{\phi =\frac{\mathrm{\pi }}{2}}$

$\boxed{3-2}$ إثبات تعبير الطاقة المخزونة في المكثف بدلالة $q\left(t\right)$ و$C$:

تعبير القدرة هو:  $P=u_c.i$  مع: $i=\frac{dq}{dt}$ 

ومنه $P=u_c.\frac{dq}{dt}$ 

بما أن: $q=C.u_c$  فإن: $u_c=\frac{q}{c}$   أي: $P=\frac{q}{C}.\frac{dq}{dt}$

$P=\frac{1}{2C}.\frac{d{q}^2}{dt}=\frac{d}{dt}\left(\frac{q^2}{2C}\right)$

بما أن: $P=\frac{d{E}_e}{dt}$  فإن تعبير الطاقة المخزونة في المكثف: 

$\boxed{E_e=\frac{1}{2}.\frac{q^2}{C}}$

$\boxed{4-2}$

$\boxed{1-4-2}$ حساب $E_{emax}$

لدينا: $E_e=\frac{1}{2}.\frac{q^2}{C_0}$  مع:  $q=C_0.u_c$ 

تعبير الطاقة الكهربائية يصبح: $E_e=\frac{1}{2}.\frac{{\left(C.u_c\right)}^2}{C_0}=\frac{1}{2}{C}_0.u_c^2$

عند اللحظة $t=0$  لدينا:  $u_c\left(0\right)=E$  تكون الطاقة الكهربائية قصوى وبالتالي: $E_{e max}=\frac{1}{2}.C_0.E^2$

ت.ع:

$\boxed{E_{e max}=\frac{1}{2}\times 5.{10}^{-6}\times 6^2=9.{10}^{-5 }J}$

$\boxed{2-4-2}$ إيجاد قيمة $I_m$  بالاعتماد على الدراسة الطاقية

الطاقة الكلية $E_T$ المخزونة في الدارة تساوي:

$E_T=E_e+E_m=\frac{1}{2}.C_0.u_c^2+\frac{1}{2}.L.i^2$

عندما تكون الطاقة الكهربائية المخزونة في المكثف قصوية تكون الطاقة المغناطيسية المخزونة في الوشيعة دنوية والعكس صحيح

 $E_T=E_{e max}=\frac{1}{2}.L.I_m^2$

ومنه:  $I_m^2=\frac{2E_{e max}}{L}$  أي:  $I_m=\sqrt{\frac{2E_{e max}}{L}}$

تحديد $L$:
تعبير الدور الخاص $T_0$  هو: $T_0=2\mathrm{\pi }\sqrt{{\mathrm{L}}_0}.{\mathrm{C}}_0$  ومنه: $L_0.C_0=\frac{T_0^2}{4{\mathrm{\pi }}^2}$

وبالتالي: $L_0=\frac{T_0^2}{4{\mathrm{\pi }}^2.{\mathrm{C}}_0}$

نعوض في تعبير $I_m$

$$\begin{gathered} I_m=\sqrt{\frac{2E_{e max}}{T_0^2}}.4{\mathrm{\pi }}^2.{\mathrm{C}}_0 \\ \Rightarrow {\mathrm{I}}_{\mathrm{m}}=\frac{2\mathrm{\pi }}{{\mathrm{T}}_0}.\sqrt{2{\mathrm{E}}_{\mathrm{e} \max }}.{\mathrm{C}}_0 \end{gathered}$$

مبيانيا الدور الخاص هو: $T_0=5 ms$  

ومنه:

$\boxed{I_m=\frac{2\mathrm{\pi }}{5.{10}^{-3}}\times \sqrt{2\times 9.{10}^{-5}\times 5.{10}^{-6}}\approx 3,77.{10}^{-2} A}$

$\boxed{II}$ التذبذبات القسرية في دارة متوالية  $RLC$

$\boxed{1}$

$\boxed{1-1}$ تعيين المنحنى الممثل للتوتر $u_R\left(t\right)$:

نعلم أن: $Z>R$  وبالتالي: $Z.I_m>R.I_m$  أي: $u_{AB m}>u_{R m}$

حسب الشكل $5$ المنحنى $\left(1\right)$ يمثل التوتر $u_R\left(t\right)$

$\boxed{2-1}$ تحديد قيمة $Z$:

لدينا: $\left(1\right) u_{R m}=R.I_m$ و $\left(2\right) u_{AB m}=Z.I_m$

ومنه: $\frac{\left(1\right)}{\left(2\right)}\to \frac{Z.I_m}{R.I_m}=\frac{u_{AB m}}{u_{R m}}$ 

نحصل على: $Z=R.\frac{u_{AB m}}{u_{R m}}$

باستعمال الشكل $5$ نجد: $u_{R m}=3 V$  و $u_{AB m}=6 V$

ت.ع:

$\boxed{Z=20\times \frac{6}{3}=40\Omega }$

$\boxed{3-1}$ التعبير العددي لشدة التيار $i\left(t\right)$:

لدينا: $i\left(t\right)=I_m\cos \left(\frac{2\mathrm{\pi }}{T_0}.t+\phi \right)$

تحديد $T_0$:

حسب الشكل $5$ الدور الخاص:  $T_0=1,25ms\times 4=5 ms$  ومنه: $\frac{2\mathrm{\pi }}{T_0}=\frac{2\mathrm{\pi }}{5.{10}^{-3}}=400\mathrm{\pi }$

تحديد $\phi$:

بما أن التوتر $u\left(t\right)$ متقدم في الطور على شدة التيار $i\left(t\right)$  وبما أن طور التوتر $u\left(t\right)$ منعدم فإن $\phi <0$

لدينا: $\left|\phi \right|=\frac{2\mathrm{\pi }}{T_0}.\tau$ 

ت.ع: $\phi =-400\mathrm{\pi }\times 1,25.{10}^{-3}=-\frac{\mathrm{\pi }}{4}$

تحديد $I_m$:

لدينا: $u_{R m}=R.I_m$  أي:    $I_m=\frac{u_{R m}}{R}=\frac{3}{20}=0,15 A$

تعبير $i\left(t\right)$  هو:

$\boxed{i\left(t\right)=0,15 \cos \left(400\mathrm{\pi }.\mathrm{t}-\frac{\mathrm{\pi }}{4}\right)}$

$\boxed{2}$

$\boxed{1-2}$ إثبات أن الدارة في حالة رنين:

لإثبات أن الدارة في حالة رنين كهربائي يجب التحقق من:  $Z=R$

يشير الفولطمتر الى التوتر الفعال بين مربطي الموصل الأومي: $U_R=R.I_{eff}$ 

أي: $I_{eff}=\frac{U_R}{R}=\frac{3}{20}=0,15 A$

نحدد ممانعة الدارة $Z$:

لدينا: $u_{AB m}=Z.I_m$  أي: $Z=\frac{u_{AB m}}{I_m}=\frac{U_m}{\sqrt{2}.I_{eff}}$ 

ت.ع:

$Z=\frac{6}{0,15\times \sqrt{2}}=28,28\approx 28,3\Omega$

نلاحظ أن:  $R+r_b=20+8,3=28,3\Omega$  ونستنتج إذن أن الدارة في حالة رنين

$\boxed{2-2}$ تحديد $L$:

عند الرنين يكون: $L\omega =\frac{1}{C_2.\omega }$ 

أي: $L=\frac{1}{C_2.{\omega }^2}$     مع: $\omega =2\mathrm{\pi N}=\frac{2\mathrm{\pi }}{\mathrm{T}}$

إذن $L=\frac{T^2}{4{\mathrm{\pi }}^2.{\mathrm{C}}_2}$  

ت.ع:

$\boxed{L=\frac{{\left(5.{10}^{-3}\right)}^2}{4{\mathrm{\pi }}^2\times 10.{10}^{-6}}=63,3 mH}$

الميكانيك

(الجزءان الأول والثاني مستقلان)

الجزء الأول: حركة كرة مضرب في مجال الثقالة المنتظم

$\boxed{1}$ إثبات التعبير العددي لمعادلة المسار $z=f\left(x\right)$

المجموعة المدروسة  {كرة المضرب}

تخضع الكرة لوزنها $\overrightarrow{P}$  فقط

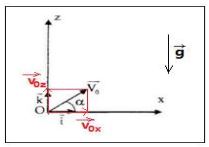
نطبق القانون الثاني لنيوتن في المعلم $\left(O,\overrightarrow{i},\overrightarrow{k}\right)$ الذي نعتبره غاليليا  $\overrightarrow{P}=m.{\overrightarrow{a}}_G$

$m.\overrightarrow{g}=m.{\overrightarrow{a}}_G\iff {\overrightarrow{a}}_G=\overrightarrow{g}$

الشروط البدئية عند $t=0$:

$$\begin{gathered} {\overrightarrow{V}}_0\left\{\begin{array}{l}{V}_{0x}=V_{0 \cos a}\\ V_{0x}=V_{0 \sin a}\end{array}\right. \\ \overrightarrow{g}\left\{\begin{array}{l}{g}_x=0\\ g_z=-g\end{array}\right. \\ {\overrightarrow{OG}}_0\left\{\begin{array}{l}{x}_0=0\\ z_0=0\end{array}\right. \end{gathered}$$

الإسقاط على $O_x$:

  $\Leftarrow a_x=0$ الحركة مستقيمية منتظمة على المحور $O_x$

المعادلة الزمنية: $x\left(t\right)=\left(V_0\cos a\right)t+x_0=\left(V_0\cos a\right)t$

الاسقاط على $O_z$:

$\Leftarrow a_y=-g=Cte$  الحركة مستقيمية متغيرة بانتظام على $O_z$

المعادلة الزمنية:

$$\begin{gathered} z\left(t\right)=\frac{1}{2}{a}_z{t}^2+V_{0z}t+z_0 \\ z\left(t\right)=-\frac{1}{2}g{t}^2+\left(V_0\sin a\right)t \end{gathered}$$

استنتاج معادلة المسار:

$x=\left(V_0\cos a\right)t \Rightarrow t=\frac{x}{V_0\cos a}$

نعوض $t$ في المعادلة  $z\left(t\right)$:

$$\begin{gathered} z\left(x\right)=-\frac{1}{2}g{\left(\frac{x}{V_0\cos a}\right)}^2+\left(V_0\sin a\right)\frac{x}{V_0\cos a} \\ z\left(x\right)=-\frac{g}{2V_0^2{\cos }^{2}a}{x}^2+x.\tan a \end{gathered}$$

ت.ع

$$\begin{gathered} z\left(x\right)=-\frac{9,8}{2\times {13}^2\times {\cos }^2\left(45°\right)}{x}^2+x.\tan \left(45°\right) \\ \boxed{z\left(x\right)=-5,8.{10}^{-2}.x^2+x} \end{gathered}$$

 

$\boxed{2}$ ليتمكن اللاعب من اعتراض الكرة يجب أن يكون:  $z\left(d+D\right)+h\le H$

حساب $z\left(D+d\right)$:

$z{\left(D+d\right)}^2=-5,8.{10}^{-2}.{\left(D+d\right)}^2+D+d$

ت.ع:

$z\left(D+d\right)=-5,8.{10}^{-2}.{\left(13+1\right)}^2+13+1=2,63m$

الارتفاع الذي تمر فيه الكرة فوق رأس اللاعب هو $z\left(D+d\right)+h=2,63+0,7=3,33m$

بما أن: $z\left(D+d\right)+h>H=3m$  فإن اللاعب لن يتمكن من اعتراض الكرة

 

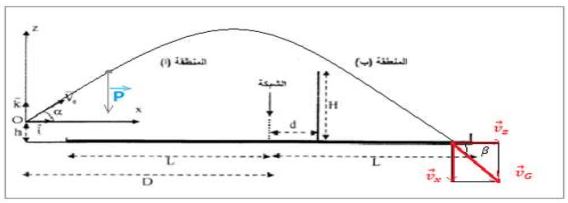
$\boxed{3}$ التحقق من أن الكرة تسقط في المنطقة $\boxed{ب}$

عند سقوط الكرة على سطح الأرض يكون: $z=-h$

نعوض في معادلة المسار نحصل على:$-h=-5,8.{10}^{-2}.x^2+x$

أي:  $-5,8.{10}^{-2}.x^2+x+0,7=0$

يوجد حلان لهذه المعادلة:

$$\begin{gathered} x_{1,2}=\frac{-1\pm \sqrt{1^2-4\times \left(-5,8.{10}^{-2}\right)\times 0,7}}{2\times \left(-5,8.{10}^{-2}\right)} \\ \Rightarrow \left\{\begin{array}{l}{x}_1=17,58 m\\ x_2=-0,34 m <0\end{array}\right. \end{gathered}$$

أفصول نقطة سقوط كرة المضرب موجبة إذن الحل الأنسب هو $x_1=17,83 m$

لتسقط الكرة في المنطقة $\boxed{ب}$  يجب أن أن ينتمي أفصولها الى المجال: $x_1<D+L=12+13=25 m$

بما أن $x_1<25 m$  فإن الكرة تسقط في المنطقة $\boxed{ب}$

$\boxed{4}$ تحديد إحداثيات متجهة سرعة $G$  لحظة سقوط الكرة على سطح الأرض

ليكن $t_1$  مدة السقوط  و$x_1$  أفصوله

لدينا $x_1=\left(V_0\cos a\right)t_1 \Rightarrow t_1=\frac{x_1}{V_0\cos a}$  مع: $x_1=17,83 m$

إحداثيات السرعة على المحور $O_x$ هي $v_{x1}=V_0\cos a$

ت.ع:

$v_{x1}=13\times \cos \left(45°\right)=9,19 m.s^{-1}$

إحداثيات السرعة على المحور $O_z$ هي $v_{z1}=-g{t}_1+V_0\sin a$  أي:  $v_{z1}=-g.\frac{x_1}{V_0\cos a}+V_0\sin a$

ت.ع:

$v_{z1}=-9,8\times \frac{17,58}{13\times \cos \left(45°\right)}+13\times \sin \left(45°\right)=-9,55 m.s^{-1}$

متجهةالسرعة تكون زاوية $\beta$  مع الخط الإفقي حيث:

$$\begin{gathered} \tan \beta =\left|\frac{v_{z1}}{v_{x1}}\right| \\ \Rightarrow \beta ={\tan }^{-1}\left|\frac{-9,55}{9,19}\right|=46,1° \end{gathered}$$

متجهة السرعة $\overrightarrow{v_G}$  تكون زاوية $\beta =46,1°$  مع المحور الافقي (انظر الشكل أعلاه)

$\boxed{5}$ إيجاد القيمتين الحديتين للسرعة البدئية  $v_0$:

لكي تسقط الكرة في المنطقة $\boxed{ب}$: القيمة الحدية للأفصول $x$ هو: $x=D+L$ والأنسوب $z$ هو: $z\left(D+L\right)=-h$

نعوض في معادلة المسار فنحصل على

 $$\begin{gathered} z\left(D+L\right)=-h \\ \Rightarrow -\frac{g}{2V_0^2{\cos }^{2}a}{\left(D+L\right)}^2+\left(D+L\right).\tan a=-h \\ \Rightarrow \frac{g}{2V_0^2{\cos }^{2}a}{\left(D+L\right)}^2=\left(D+L\right).\tan a+h \end{gathered}$$

أي:

$$\begin{gathered} v_0=\sqrt{\frac{ g{\left(D+L\right)}^2 }{2\left[\left(D+L\right).\tan a+h\right].{\cos }^{2}a}} \\ {v}_0=\frac{D+L}{\cos a}\sqrt{\frac{ g}{2\left[\left(D+L\right).\tan a+h\right]}} \end{gathered}$$

ت.ع: 

  $$\begin{gathered} v_0=\frac{13+12}{\cos \left(45°\right)}\sqrt{\frac{9,8}{2\times \left[\left(13+12\right)\times \tan \left(45°\right)+0,7\right]}} \\ \boxed{v_0=15,44 m.s^{-1}} \end{gathered}$$

لكي تمر الكرة فوق اللاعب المنافس يجب أن يكون الأفصول: $x=D+d$   والأنسوب الحدي هو:  $z\left(D+d\right)+h=H$

نعوض في معادلة المسار فنحصل على

$$\begin{gathered} -\frac{g}{2V_0^2{\cos }^{2}a}{\left(D+d\right)}^2+\left(D+d\right).\tan a+h=H \\ \Rightarrow \frac{g}{2V_0^2{\cos }^{2}a}{\left(D+d\right)}^2=\left(D+d\right).\tan a+h-H \end{gathered}$$

ومنه: $$\begin{gathered} v_0=\sqrt{\frac{ g{\left(D+d\right)}^2 }{2\left[\left(D+d\right).\tan a+h-H\right].{\cos }^{2}a}} \\ \boxed{v_0=\frac{D+d}{\cos a}\sqrt{\frac{ g}{2\left[\left(D+d\right).\tan a+h-H\right]}}} \end{gathered}$$

ت.ع:

$$\begin{gathered} v_0=\frac{ 13+1}{\cos \left(45°\right)}\sqrt{\frac{ 9,8}{2\times \left[\left(13+1\right)\times \tan \left(45°\right)+0,7-3\right]}} \\ \boxed{v_0=12,81 m.s^{-1}} \end{gathered}$$

الجزء الثاني: دراسة حركة نواس وازن

$\boxed{1}$ حالة النظام الدوري

$\boxed{1-1}$ إثبات المعادلة التفاضلية التي يحققها الأفصول الزاوي $\theta$:

المجموعة المدروسة: {النواس الوازن}

جرد القوى: $\overrightarrow{P}$ :

وزن النواس و$\overrightarrow{R}$: تأثير محور الدوران $\left(∆\right)$

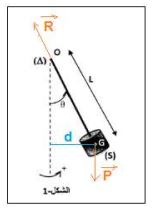
تطبيق العلاقة الاساسية للديناميك في حالة الدوران:

$$\begin{gathered} \sum M_{∆}\left(\overrightarrow{F}\right)=J_{∆}.\ddot{\theta } \\ \Rightarrow M_{∆}\left(\overrightarrow{P}\right)+M_{∆}\left(\overrightarrow{R}\right)=J_{∆}.\ddot{\theta } \left(1\right) \end{gathered}$$

  $M_{∆}\left(\overrightarrow{R}\right)=0$    و$M_{∆}\left(\overrightarrow{P}\right)=-Pd$ مع: $d=L.\sin \theta$  

نعوض في المعادلة $\left(1\right)$ : 

$-m.g.L.\sin \theta =J_{∆}.\ddot{\theta }$

بالنسبة للزوايا الصغيرة نأخذ: $\sin \theta \simeq \theta$ المعادلة التفاضلية تكتب:  $J_{∆}.\ddot{\theta }+m.g.L.\sin \theta =0$

إذن

$\boxed{\ddot{\theta }+\frac{m.g.L}{J_{∆}}.\theta =0}$

$\boxed{2-1}$ إيجاد تعبير الدور الخاص $T_0$:

حل المعادلة التفاضلية يكتب: $\theta ={\theta }_m\cos \left(\frac{2\mathrm{\pi }}{T_0}.t\right)$

ومنه: $\dot{\theta }=-\frac{2\mathrm{\pi }}{T_0}.{\theta }_m\sin \left(\frac{2\mathrm{\pi }}{T_0}.t\right)$ 

وبالتالي: $\ddot{\theta }=-{\left(\frac{2\mathrm{\pi }}{T_0}\right)}^2.{\theta }_m\cos \left(\frac{2\mathrm{\pi }}{T_0}.t\right)=-{\left(\frac{2\mathrm{\pi }}{T_0}\right)}^2\theta$

نعوض في المعادلة التفاضلية:   $-{\left(\frac{2\mathrm{\pi }}{T_0}\right)}^2\theta +\frac{\mathrm{m}.\mathrm{g}.\mathrm{L}}{J_{∆}}.\theta =0$ 

أي:  $\underset{\ne 0}{\underbrace{\theta }}\left[\underset{=0}{\underbrace{-{\left(\frac{2\mathrm{\pi }}{T_0}\right)}^2+\frac{m.g.L}{J_{∆}}}}\right]=0$

وبالتالي: $-{\left(\frac{2\mathrm{\pi }}{T_0}\right)}^2+\frac{\mathrm{m}.\mathrm{g}.\mathrm{L}}{J_{∆}}=0$

$\frac{2\mathrm{\pi }}{T_0}=\sqrt{\frac{\mathrm{m}.\mathrm{g}.\mathrm{L}}{J_{∆}}}$   أو:  $\frac{{\mathrm{T}}_0}{2\mathrm{\pi }}=\sqrt{\frac{{\mathrm{J}}_{∆}}{\mathrm{m}.\mathrm{g}.\mathrm{L}}}$

نستنتج تعبير الدور الخاص:

$\boxed{{\mathrm{T}}_0=2\mathrm{\pi }\sqrt{\frac{{\mathrm{J}}_{∆}}{\mathrm{m}.\mathrm{g}.\mathrm{L}}}}$

$\boxed{3-1}$ التحقق من أن لتعبير الدور الخاص بعد زمني:

لدينا: ${\mathrm{T}}_0=2\mathrm{\pi }\sqrt{\frac{{\mathrm{J}}_{∆}}{\mathrm{m}.\mathrm{g}.\mathrm{L}}}$

وبالتالي: ${\left[{\mathrm{T}}_0\right]}^2=\frac{\left[{\mathrm{J}}_{∆}\right]}{\left[\mathrm{m}\right].\left[\mathrm{g}\right].\left[\mathrm{L}\right]}$ مع: $J_{∆}=\sum m{r}^2$

أي:  $\left[{\mathrm{J}}_{∆}\right]=\left[\mathrm{m}\right]{\left[\mathrm{L}\right]}^2$

$\left[g\right]=\frac{\left[L\right]}{{\left[t\right]}^2}$

$$\begin{gathered} {\left[{\mathrm{T}}_0\right]}^2=\frac{\left[\mathrm{m}\right]{\left[\mathrm{L}\right]}^2}{\left[\mathrm{m}\right].\left[\mathrm{L}\right].{\left[t\right]}^{-2}.\left[\mathrm{L}\right]}={\left[t\right]}^2 \\ \Rightarrow \left[T\right]=\left[t\right] \end{gathered}$$

نستنتج أن للدور الخاص $T_0$ بعد زمني

$\boxed{4-1}$ تحديد قيمة ${\mathrm{J}}_{∆}$:

لدينا: $\frac{{\mathrm{T}}_0}{2\mathrm{\pi }}=\sqrt{\frac{{\mathrm{J}}_{∆}}{\mathrm{m}.\mathrm{g}.\mathrm{L}}}$ 

أي:  ${\left(\frac{{\mathrm{T}}_0}{2\mathrm{\pi }}\right)}^2=\frac{{\mathrm{J}}_{∆}}{\mathrm{m}.\mathrm{g}.\mathrm{L}}$

أي:  ${\mathrm{J}}_{∆}=\frac{{\mathrm{T}}_0^2.\mathrm{m}.\mathrm{g}.\mathrm{L}}{4{\mathrm{\pi }}^2}$

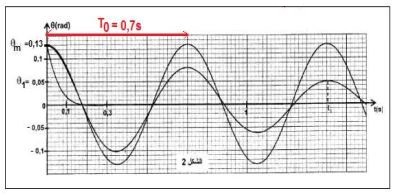
مبيانيا من الشكل $2$ : الدور الخاص: $T_0=0,7 s$

ت.ع:

$\boxed{J_{∆}=\frac{0,7^2\times 0,4\times 0,5\times 9,8}{4{\mathrm{\pi }}^2}=2,4.{10}^{-2} kg.m^{2 }}$

$\boxed{5-1}$ إيجاد تعبير الطاقة الحركية للمتذبذب:

الطاقة الحركية للمتذبذب تكتب: $E_c=\frac{1}{2}{J}_{∆}.{\dot{\theta }}^2$

مع: $\dot{\theta }=-\frac{2\mathrm{\pi }}{T_0}.{\theta }_m\sin \left(\frac{2\mathrm{\pi }}{T_0}.t\right)$

ومنه: $E_c=\frac{1}{2}{J}_{∆}.{\left[-\frac{2\mathrm{\pi }}{T_0}.{\theta }_m\sin \left(\frac{2\mathrm{\pi }}{T_0}.t\frac{2\mathrm{\pi }}{T_0}\right)\right]}^2$ 

أي: $E_c=\frac{1}{2}.J_{∆}.{\left(\frac{2\mathrm{\pi }}{T_0}\right)}^2.{\theta }_m^2.{\sin }^2\left(\frac{2\mathrm{\pi }}{T_0}\right)$

نعلم أن:  $\frac{2\mathrm{\pi }}{T_0}=\sqrt{\frac{m.g.L}{J_{∆}}}$  أي: ${\left(\frac{2\mathrm{\pi }}{T_0}\right)}^2=\frac{m.g.L}{J_{∆}}$

نعوض في تعبير $E_c$  نجد:

$$\begin{gathered} E_c=\frac{1}{2}.m.g.L.{\theta }_m^2\left[1-{\cos }^2\left(\frac{2\mathrm{\pi }}{T_0}\right)\right] \\ {E}_c=\frac{1}{2}.m.g.L\left[{\theta }_m^2-\underset{=\theta }{\underbrace{{\theta }_m^2{\cos }^2\left(\frac{2\mathrm{\pi }}{T_0}\right)}}\right] \\ {E}_c=\frac{1}{2}m.g.L.\left({\theta }_m^2-{\theta }^2\right) \end{gathered}$$

مبيانيا نجد:  ${\theta }_m=0,13 rad$ 

عند موضع التوازن يكون $\theta =0$

ت.ع:

$\boxed{E_c=\frac{1}{2}\times 0,4\times 9,8\times 0,5\times \left(0,{13}^2-0\right)=1,66.{10}^{-2} J}$

$\boxed{2}$ إيجاد تغير الطاقة الميكانيكية في حالة النظام شبه الدوري

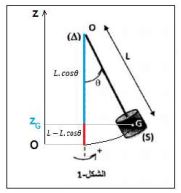
تعبير طاقة الوضع الثقالية:  $E_p=m.g.z+C$ 

الحالة المرجعية  $E_p=0$ عند:  $z=0$  ومنه: $C=0$

وبالتالي: $E_p=m.g.z$   مع:  $\mathrm{z}=\mathrm{L}\left(1-\mathrm{cos\theta }\right)$ 

باعتبار الزاوية $\theta$  صغيرة نكتب: $\cos \theta \simeq 1-\frac{{\theta }^2}{2}$

ومنه نكتب: $z=L\left(1-\left(1-\frac{{\theta }^2}{2}\right)\right)=L.\frac{{\theta }^2}{2}$

تعبير $E_p$  هو:  $E_p=m.g.l.\frac{{\theta }^2}{2}$

تغير طاقة الوضع الثقالية

$$\begin{gathered} ∆E_p=E_p\left(t=t_1\right)-E_p\left(t=0\right) \\ ∆E_p=m.g.L\left(\frac{{\theta }_1^2}{2}-\frac{{\theta }_m^2}{2}\right) \\ ∆E_p=\frac{1}{2}m.g.L.\left({\theta }_1^2-{\theta }_m^2\right) \end{gathered}$$

من خلال منحنى الشكل $2$ أعلاه نلاحظ عند اللحظتين: $t=0$  و $t=t_1$ تكون $\theta$  قصوية وبالتالي تكون السرعة منعدمة وبالتالي الطاقة الحركية منعدمة

أي: $E_c\left(t=0\right)=0$   و  $E_c\left(t=t_1\right)=0$

ومنه:  $∆E_c=E_c\left(t=t_1\right)-E_c\left(t=0\right)=0$

تغير الطاقة الميكانيكية: $∆E_m=∆E_c+∆E_p=∆E_p$

عند: $t=0$  مبيانيا نجد: $\theta ={\theta }_m=0,13 rad$ 

وعند:  $t=t_1$  نجد: ${\theta }_1=0,05 rad$

ت.ع:

$$\begin{gathered} ∆E_m=\frac{1}{2}\times 0,4\times 9,8\times 0,5\times \left(0,{05}^2-0,{13}^2\right)=0,0141 J \\ \Rightarrow \boxed{∆E_m=-1,41.{10}^{-2} J} \end{gathered}$$