الامتحان الوطني الموحد 2016 الدورة الإستدراكية: الموضوع والتصحيح

1
التمرين 1
الكيمياء

الجزء الأول: دراسة العمود ألومنيوم – زنك

تعتبر الأعمدة الكيميائية أحد تطبيقات تفاعلات الأكسدة–اختزال، أثناء اشتغالها، يتحول جزء من الطاقة الكيميائية الناتجة عن هذه التفاعلات الى طاقة كهربائية.

ننجز العمود ألومنيوم–زنك بغمر صفيحة من الألومنيوم في كأس تحتوي على الحجم $V = 100 m L$ من محلول مائي لكلورور الألومنيوم $A l_{(a q)}^{3 +} + C l_{(a q)}^{-}$ تركيزه المولي البدئي $C_{1} = [A l_{(a q)}^{3 +}] = 4, 5 . 10^{- 2} m o l . L^{- 1}$ وصفيحة من الزنك في كأس اخر تحتوي على الحجم $V = 100 m L$ من محلول مائي لكبريتات الزنك $Z n_{(a q)}^{2 +} + S O_{4 (a q)}^{2 -}$ تركيزه المولي البدئي $C_{2} = [Z n_{(a q)}^{2 +}] = 4, 5 . 10^{- 2} m o l . L^{- 1}$ ، نوصل المحلولين بقنطرة ملحية. نركب بين قطبي العمود موصلا أوميا $(D)$ وأمبيرمترا و قاطعا للتيار (لشكل $1$ )

معطيات:

كتلة الجزء المغمور من صفيحة الألومنيوم في محلول كلورور الألومنيوم لحظة إغلاق الدارة هي $m_{0} = 1, 35 g$

الكتلة المولية للألومنيوم $M (A l) = 27 g . m o l^{- 1}$

ثابتة فرادي $1 F = 9, 65 . 10^{4} C . m o l^{- 1}$

ثابتة التوازن المقرونة بمعادلة التفاعل $2 A l_{(a q)}^{3 +} + 3 Z n_{(s)} ⇌ 2 A l_{(s)} + 3 Z n_{(a q)}^{2 +}$ هي $K = 10^{- 90}$ عند $25 ° C$

نغلق القاطع $k$ عند اللحظة $t = 0$ ، فيمر في الدارة تيار كهربائي شدته $I$ نعتبرها ثابتة $I = 10 m A$

$1$ احسب خارج التفاعل $Q_{r i}$ في الحالة البدئية و استنتج منحى التطور التلقائي للمجموعة الكيميائية

$2$ مثل التبيانة الاصطلاحية للعمود المدروس معللا قطبيته

$3$ أوجد عندما يستهلك العمود كليا:

$1 - 3$ تركيز أيونات الألومنيوم في محلول كلورور الألومنيوم

$2 - 3$ المدة الزمنية $Δ t$ لاشتغال العمود

الجزء الثاني: تصنيع إستر وتفاعل بنزوات الصوديوم مع حمض

يستعمل بنزوات الصوديوم $(C_{6} H_{5} C O O N a)$ في الصناعات الغذائية كمادة حافظة وذلك لخصائصه المضادة للبكتيريا

نتطرق في هذا الجزء الى دراسة تصنيع إستر انطلاقا من تفاعل حمض البنزويك مع الميثانول والى دراسة تفاعل بنزوات الصوديوم $C_{6} H_{5} C O O_{(a q)}^{-} + N a_{(a q)}^{+}$ مع حمض الإيثانويك $C H_{3} C O O H$

معطيات:

عند $25 ° C$ : $p K_{A 1} (\frac{C_{6} H_{5} C O O H}{C_{6} H_{5} C O O^{-}}) = 4, 2$ و $p K_{A 2} (\frac{C H_{3} C O O H}{C H_{3} C O O^{-}}) = 4, 8$

الكتلة الحجمية للميثانول: $ρ = 0, 8 g . m L^{- 1}$

الكتلة المولية للميثانول $M (C H_{3} O H) = 32 g . m o l^{- 1}$

الكتلة المولية لحمض البنزويك $M (C_{6} H_{5} C O O H) = 122 g . m o l^{- 1}$

$1$ دراسة تصنيع إستر

لتصنيع إستر، نمزج في حوجلة كمية من حمض البنزويك $C_{6} H_{5} C O O H$ كتلتها $m = 12, 2 g$ وحجما $V = 8 m L$ من الميثانول $C H_{3} O H$ ونضيف قطرات من حمض الكبريتيك وبعض حصى الخفان، ثم نسخن الخليط بالارتداد عند درجة حرارة $θ$

$1 - 1$ علل اختيار التسخين بالارتداد

$2 - 1$ اكتب المعادلة الكيميائية المنمذجة للتفاعل الذي يحدث

$3 - 1$ يمثل منحنى الشكل $2$ تطور كمية مادة الإستر المتكون خلال الزمن

$1 - 3 - 1$ اختر الاقتراح الصحيح من بين الاقتراحات التالية:

السرعة الحجمية لتفاعل الأسترة:

منعدمة عند بداية التفاعل

قصوية عند التوازن

قصوية عند بداية التفاعل

تتناقص كلما ازداد تركيز أحد المتفاعلات

تتناقص عند إضافة حفاز الى الخليط التفاعلي

$2 - 3 - 1$ عرف زمن نصف التفاعل وحدد قيمته

$3 - 3 - 1$ حدد مردود التفاعل

$2$ دراسة تفاعل بنزوات الصوديوم مع حمض الإيثانويك

نمزج عند ، حجما من محلول مائي لبنزوات الصوديوم تركيزه المولي مع حجم من محلول مائي لحمض الإيثانويك تركيزه المولي

$1 - 2$ اكتب المعادلة المنمذجة للتفاعل الذي يحدث

$2 - 2$ بين أن ثابتة التوازن المقرونة بهذا التفاعل هي $K = 0, 25$

$3 - 2$ عبر عن نسبة التقدم النهائي $τ$ لهذا التفاعل بدلالة $K$

$4 - 2$ أوجد تعبير $p H$ الخليط التفاعلي بدلالة $p K_{A 1}$ و $τ$ واحسب قيمته

الكيمياء

الجزء الأول: دراسة العمود ألومنيوم – زنك

$1$ حساب خارج التفاعل $Q_{r i}$ في الحالة البدئية

$2 A l_{(a q)}^{3 +} + 3 Z n_{(s)} ⇌ 2 A l_{(s)} + 3 Z n_{(a q)}^{2 +}$

ثابتة التوازن المقرونة بهذا التفاعل هي $K = 10^{- 90}$

نلاحظ أن $Q_{r i} > K$ , إذن تنتقل المجموعة الكيميائية تلقائيا في المنحى $(2)$ (المنحى غير المباشر أي منحى تكون $Z n$ وأيونات $A l^{3 +}$ )

$2$ التبيانة الاصطلاحية للعمود

بما أن فلز الالومنيوم يتأكسد خلال اشتغال العمود حسب نصف المعادلة $A l_{(s)} ⇄ A l_{(a q)}^{3 +} + 3 e^{-}$ فهو يمثل الأنود أي القطب السالب للعمود ومنه فالتبيانة الاصطلاحية هي $(-) \frac{A l_{(s)}}{A l_{(a q)}^{3 +}} / / \frac{Z n_{(a q)}^{2 +}}{Z n_{(s)}} (+)$

$3$ عندما يستهلك العمود كليا

$1 - 3$ تركيز أيونات الألومنيوم

الجدول الوصفي

تحديد التقدم الأقصى

$A l$ متفاعل محد نكتب $n_{0} (A l) - 2 x_{m a x} = 0$ أي $x_{m a x 1} = \frac{n_{0} (A l)}{2} = \frac{m_{0}}{2 M (A l)} = 2, 5 . 10^{- 2} m o l$

$Z n^{2 +}$ متفاعل محد نكتب $C_{2} . V - 3 x_{m a x} = 0$ أي $x_{m a x 2} = \frac{C_{2} . V}{3} = 1, 5 . 10^{- 3} m o l$

و بالتالي التقدم الأقصى هو $x_{m a x} = 1, 5 . 10^{- 3} m o l$

حسب الجدول الوصفي تركيز أيونات الألومنيوم

${[A l^{3 +}]}_{f} = \frac{C_{1} . V + 2 x_{m a x}}{V} = 7, 5 . 10^{- 2} m o l . L^{- 1}$

$2 - 3$ المدة الزمنية $Δ t$ لاشتغال العمود

$\{\begin{cases} n (e^{-}) = 6 x_{m a x} \\ n (e^{-}) = \frac{I . Δ t}{F} \end{cases} \Rightarrow Δ t = \frac{6 x_{m a x} . F}{I} = 86850 s \Rightarrow Δ t = 24 h 7 m i n 30 s$

الجزء الثاني: تصنيع وتفاعل بنزوات الصوديوم مع حمض

$1$ دراسة تصنيع إستر

$1 - 1$ تعليل اختيار التسخين بالارتداد

التسخين يسرع التفاعل والارتداد يحافظ على كمية مادة المتفاعلات والنواتج

$2 - 1$ معادلة التفاعل:

$C_{6} H_{5} C O O H + C H_{3} O H ⇄ C_{6} H_{5} C O O C H_{3} + H_{2} O$

$3 - 1$

$1 - 3 - 1$ اختيار الاقتراح الصحيح

السرعة الحجمية لتفاعل الأسترة

منعدمة عند بداية التفاعل: خطأ

قصوية عند التوازن: خطأ

قصوية عند بداية التفاعل: صحيح

تتناقص كلما ازداد تركيز أحد المتفاعلات: خطأ

تتناقص عند إضافة حفاز الى خليط التفاعل: خطأ

$2 - 3 - 1$ تعريف زمن نصف التفاعل

زمن نصف التفاعل $t_{\frac{1}{2}}$ هو المدة الزمنية التي يصل فيها تقدم التفاعل الى نصف قيمته النهائية $x (t_{\frac{1}{2}}) = \frac{x_{f}}{2}$

تحديد قيمة $t_{\frac{1}{2}}$ مبيانيا

حسب مبيان الشكل 2 لدينا $x_{f} = n_{f} = 84 m m o l$ أي $x (t_{\frac{1}{2}}) = 42 m m o l$

أفصول $x (t_{\frac{1}{2}})$ هو $t_{\frac{1}{2}} = 6 m i n$

$3 - 3 - 1$ مردود التفاعل

الجدول الوصفي:

تحديد التقدم الأقصى $x_{m a x}$

الحمض متفاعل محد $n_{1} - x_{m a x 1} = 0$

أي

$n_{1} = n_{i} (C_{6} H_{5} C O O H) n_{1} = x_{m a x 1} n_{1} = \frac{m}{M (C_{6} H_{5} C O O H)} n_{1} = 0, 1 m o l$

الكحول متفاعل محد $n_{2} - x_{m a x 2} = 0$

أي $n_{2} = n_{i} (C H_{3} O H) = x_{m a x 2} = \frac{ρ . V}{M (C H_{3} O H)} = 0, 2 m o l$

التقدم الأقصى هو $x_{m a x} = 0, 1 m o l$ والتقدم النهائي هو $x_{f} = 84 m m o l$

تعبير مردود التفاعل

$r = \frac{n_{e x p}}{n_{t h}} = \frac{x_{f}}{x_{m a x}} = 0, 84 = 84 %$

$2$ دراسة تفاعل بنزوات الصوديوم مع الحمض

$1 - 2$ معادلة التفاعل

$C_{6} H_{5} C O O_{(a q)}^{-} + C H_{3} C O O H_{(a q)} ⇄ C_{6} H_{5} C O O H_{(a q)} + C H_{3} C O O_{(a q)}^{-}$

$2 - 2$ التوصل الى قيمة $K$

$K = \frac{{[C_{6} H_{5} C O O H]}_{é q} . {[C H_{3} C O O^{-}]}_{é q}}{{[C_{6} H_{5} C O O^{-}]}_{é q} . {[C H_{3} C O O H]}_{é q}} . \frac{{[H_{3} O^{+}]}_{é q}}{{[H_{3} O^{+}]}_{é q}} K = \frac{K_{A 2}}{K_{A 1}} K = \frac{10^{- p K_{A 2}}}{10^{- p K_{A 1}}} K = 10^{p K_{A 1} - p K_{A 2}} K = 0, 25$

$3 - 2$ التعبير عن $τ$ بدلالة $K$

الجدول الوصفي:

التقدم الأقصى $x_{m a x} = C_{1} . V_{1}$

نسبة التقدم النهائي $τ = \frac{x_{f}}{x_{m a x}} = \frac{x_{f}}{C_{1} . V_{1}}$ ومنه التقدم النهائي $x_{f} = C_{1} . V_{1} . τ$

${[C_{6} H_{5} C O O H]}_{é q} = {[C H_{3} C O O^{-}]}_{é q} = \frac{x_{f}}{2 V_{1}} = \frac{C_{1} . V_{1} . τ}{2 V_{1}} = \frac{C_{1} . τ}{2}$

${[C_{6} H_{5} C O O^{-}]}_{é q} = {[C H_{3} C O O H]}_{é q} = \frac{C_{1} . V_{1} - x_{f}}{2 V_{1}} = \frac{C_{1} . (1 - τ)}{2}$

$K = \frac{{[C_{6} H_{5} C O O H]}_{é q} . {[C H_{3} C O O^{-}]}_{é q}}{{[C_{6} H_{5} C O O^{-}]}_{é q} . {[C H_{3} C O O H]}_{é q}} K = {(\frac{\frac{C_{1} . τ}{2}}{\frac{C_{1} . (1 - τ)}{2}})}^{2} K = {(\frac{τ}{1 - τ})}^{2} \Rightarrow τ = \frac{\sqrt{K}}{1 + \sqrt{K}}$

$4 - 2$ تعبير $p H$ بدلالة $p K_{A 1}$ و $τ$

لدينا

$p H = p K_{A 1} + \log \frac{{[C_{6} H_{5} C O O^{-}]}_{é q}}{{[C_{6} H_{5} C O O H]}_{é q}} p H = p K_{A 1} + \log \frac{1 - τ}{τ} p H = p K_{A 1} + \log \sqrt{K} p H = p K_{A 1} - \frac{1}{2} \log K p H = 4, 2 - \frac{1}{2} \log (0, 25) p H = 4, 5$
2
التمرين 2
الموجات: انتشار موجة فوق صوتية

من بين تطبيقات الموجات فوق الصوتية، استعمالها في استكشاف تضاريس أعماق البحار وفي تحديد أماكن تواجد التجمعات السمكية، الشيء الذي يتطلب معرفة سرعة انتشار هذه الموجات في ماء البحر

يهدف هذا التمرين الى تحديد سرعة انتشار موجة فوق صوتية في الهواء وفي ماء البحر

$1$ تحديد سرعة انتشار موجة فوق صوتية في الهواء

نضع باعثا $E$ للموجات فوق الصوتية ومستقبلين $R_{1}$ و $R_{2}$ كما هو مبين في الشكل $1$

يرسل الباعث $E$ موجة فوق صوتية متوالية جيبية تنتشر في الهواء لتصل الى المستقبلين $R_{1}$ و $R_{2}$ . نعاين بواسطة راسم التذبذب في المدخل $Y_{1}$ الإشارة الملتقطة من طرف $R_{1}$ وفي المدخل $Y_{2}$ الإشارة الملتقطة من طرف $R_{2}$

عندما يوجد المستقبلان $R_{1}$ و $R_{2}$ معا على نفس المسافة من الباعث، يكون المنحنيان الموافقان للإشارتين الملتقطتين على توافق في الطور (الشكل $2$ )

نبعد $R_{2}$ عن $R_{1}$ فنلاحظ أن المنحنيين يصبحان غير متوافقين في الطور. باستمرار إبعاد $R_{2}$ عن $R_{1}$ يصبح المنحنيان من جديد ولرابع مرة على توافق في الطور عندما تأخذ المسافة بين $R_{1}$ و $R_{2}$ القيمة $d = 3, 4 c m$ (الشكل $1$ )

$1 - 1$ اختر الاقتراح الصحيح من بين الاقتراحات التالية:

$أ$ الموجات فوق الصوتية موجات كهرمغنطيسية

$ب$ لا تنتشر الموجات فوق الصوتية في الفراغ

$ج$ لا يمكن الحصول على ظاهرة الحيود بواسطة الموجات فوق الصوتية

$د$ تنتشر الموجات فوق الصوتية في الهواء بسرعة انتشار الضوء

$2 - 1$ حدد التردد $N$ للموجة فوق الصوتية المدروسة

$3 - 1$ تحقق أن سرعة انتشار الموجة فوق الصوتية في الهواء هي $V_{a} = 340 m . s^{- 1}$

$2$ تحديد سرعة انتشار الموجة فوق الصوتية في ماء البحر

يرسل الباعث الموجة فوق الصوتية السابقة في أنبوبين أحدهما به هواء والاخر مملوء بماء البحر (الشكل $3$ )

يلتقط المستقبل $R_{1}$ الموجات المنتشرة في الهواء ويلتقط المستقبل $R_{2}$ الموجات المنتشرة في ماء البحر

ليكن $Δ t$ التأخر الزمني لاستقبال الموجات المنتشرة في الهواء بالنسبة لاستقبال الموجات المنتشرة في ماء البحر. وليكن $l$ المسافة الفاصلة بين الباعث والمستقبلين (الشكل $3$ )

نقيس التأخر الزمني $Δ t$ بالنسبة لمسافات $l$ مختلفة بين الباعث والمستقبلين فنحصل على منحنى الشكل $4$

$1 - 2$ عبر عن $Δ t$ بدلالة $l$ و $V_{a}$ و $V_{e}$ سرعة انتشار الموجة في ماء البحر

$2 - 2$ حدد قيمة $V_{e}$

الموجات: انتشار موجة فوق صوتية

$1$ تحديد سرعة انتشار موجة فوق صوتية في الهواء

$1 - 1$ اختيار الاقتراح الصحيح

$أ$ الموجات فوق الصوتية موجات كهرمغنطيسية: خطأ

$ب$ لا تنتشر الموجات فوق الصوتية في الفراغ: صحيح

$ج$ لا يمكن الحصول على ظاهرة الحيود بواسطة الموجات فوق الصوتية: خطأ

$د$ تنتشر الموجات فوق الصوتية في الهواء بسرعة انتشار الضوء: خطأ

$2 - 1$ تحديد تردد الموجة فوق الصوتية

حسب مبيان الشكل $2$ دور الموجة $T$ هو

$2 T = 5 d i v \times 10 μ s . d i v^{- 1} = 50 μ s \Rightarrow T = 25 μ s$

تردد الموجة $N$ هو

$N = \frac{1}{T} = 40 K H z$

$3 - 1$ التحقق من سرعة انتشار الموجة في الهواء $V_{α} = λ . N$

لدينا $d = 4 λ \Rightarrow λ = \frac{d}{4}$ ومنه $V_{α} = \frac{d}{4} . N$

ت.ع $V_{α} = \frac{3, 4 . 10^{- 2}}{4} . 4 . 10^{4} = 340 m . s^{- 1}$

$2$ تحديد سرعة انتشار الموجة فوق الصوتية في ماء البحر

$1 - 2$ التعبير عن $Δ t$ بدلالة $l$ و $V_{α}$ و $V_{e}$

$\{\begin{cases} V_{α} = \frac{l}{t_{2}} \\ V_{e} = \frac{l}{t_{1}} \end{cases} \Rightarrow \{\begin{cases} t_{2} = \frac{l}{V_{α}} \\ t_{1} = \frac{l}{V_{e}} \end{cases} \Rightarrow Δ t = t_{2} - t_{1} = l (\frac{1}{V_{α}} - \frac{1}{V_{e}})$

$2 - 2$ تحديد قيمة $V_{e}$

الدالة $Δ t = f (l)$ خطية معادلتها تكتب $Δ t = k . l$

$k$ يمثل المعامل الموجه

$k = \frac{Δ (Δ t)}{Δ l} = \frac{2, 5 . 10^{- 3}}{1, 1} = 2, 27 . 10^{- 3} s . m^{- 1}$

لدينا

$Δ t = k . l = l (\frac{1}{V_{α}} - \frac{1}{V_{e}}) \Rightarrow \frac{1}{V_{α}} - \frac{1}{V_{e}} = k \Rightarrow V_{e} = \frac{1}{\frac{1}{V_{α}} - k} \approx 1490 m . s^{- 1}$
3
التمرين 3
الكهرباء

الجزء الأول: دراسة ثنائي القطب $R C$ والدارة $L C$

تعتبر الدارات $R C$ و $R L$ و $R L C$ من بين الدارات الكهربائية المستعملة في التراكيب الإلكترونية لمجموعة من الأجهزة الكهربائية. ندرس في هذا الجزء ثنائي القطب $R C$ والدارة $L C$

يتكون التركيب التجريبي الممثل في الشكل $1$ من:

مولد مؤمثل للتوتر قوته الكهرمحركة $E$

مكثفين سعتاهما $C_{1}$ و $C_{2} = 2 μ F$

موصل أومي مقاومته $R = 3 K Ω$

وشيعة معامل تحريضها $L$ ومقاومتها مهملة

قاطع التيار $K$ ذي موضعين

$1$ دراسة ثنائي القطب $R C$

نضع القاطع $K$ في الموضع $(1)$ عند لحظة نختارها أصلا للتواريخ $(t = 0)$

$1 - 1$ بين أن تعبير السعة $C_{e}$ للمكثف المكافئ لتجميع المكثفين على التوالي هو $C_{e} = \frac{C_{1} . C_{2}}{C_{1} + C_{2}}$

$2 - 1$ بين أن المعادلة التفاضلية التي يحققها التوتر $u_{2} (t)$ بين مربطي المكثف ذي السعة $C_{2}$ تكتب: $\frac{d u_{2} (t)}{d t} + \frac{1}{R . C_{e}} . u_{2} (t) = \frac{E}{R . C_{2}}$

$3 - 1$ يكتب حل هذه المعادلة التفاضلية على الشكل $u_{2} (t) = A . (1 - e^{- α t})$ . حدد تعبير كل من $A$ و $α$ بدلالة برامترات الدارة

$4 - 1$ يمثل منحنيا الشكل $2$ تطور التوترين $u_{2} (t)$ و $u_{R} (t)$

يمثل المستقيم $(T)$ المماس للمنحنى الموافق لـ $u_{2} (t)$ عند اللحظة $t = 0$

$1 - 4 - 1$ حدد قيمة:

$E أ$

$ب$ كل من $u_{2} (t)$ و $u_{1} (t)$ في النظام الدائم

$2 - 4 - 1$ بين أن $C_{1} = 4 μ F$

$2$ دراسة التذبذبات الكهربائية في الدارة $L C$

عندما يتحقق النظام الدائم، نؤرجح القاطع $K$ الى الموضع $(2)$ عند لحظة نتخذها أصلا جديدا للتواريخ $(t = 0)$

$1 - 2$ بين أن المعادلة التفاضلية التي يحققها التوتر $u_{L} (t)$ بين مربطي الوشيعة تكتب: $\frac{d^{2} u_{L} (t)}{d t^{2}} + \frac{1}{L . C_{2}} u_{L} (t) = 0$

$2 - 2$ يمثل منحنى الشكل $3$ تغيرات التوتر $u_{L} (t)$ بدلالة الزمن

$1 - 2 - 2$ حدد الطاقة الكلية $E_{t}$ للدارة

$2 - 2 - 2$ احسب الطاقة المغنطيسية $E_{m}$ المخزونة في الوشيعة عند اللحظة $t = 2, 7 m s$

الجزء الثاني: دراسة جودة تضمين الوسع

ننجز عملية تضمين الوسع بواسطة دارة متكاملة منجزة للجداء

نطبق عند المدخل $E_{1}$ للدارة المتكاملة المنجزة للجداء التوتر الحامل $p (t)$ ، وعند المدخل $E_{2}$ التوتر $s (t) + U_{0}$ حيث $s (t)$ التوتر الموافق للإشارة المراد إرسالها و $U_{0}$ المركبة المستمرة (الشكل $4$ )

نحصل عند المخرج $S$ للدارة المتكاملة المنجزة للجداء على التوتر $u (t)$ ، الموافق للإشارة المضمنة الوسع، ذي التعبير $u (t) = k . p (t) . (s (t) + U_{0})$ حيث $s (t) = S_{m} . \cos (2 {πf}_{s} t)$ و $k$ ثابتة تميز الدارة المتكاملة المنجزة للجداء

$1$ يمكن كتابة التوتر المضمن الوسع على الشكل $u (t) = A [\frac{m}{S_{m}} s (t) + 1] . \cos (2 {πf}_{p} t)$ حيث $A = k . P_{m} . U_{0}$ و $m = \frac{S_{m}}{U_{0}}$ نسبة التضمين

أوجد تعبير نسبة التضمين $m$ بدلالة $U_{m a x}$ و $U_{m i n}$ مع $U_{m a x}$ القيمة القصوية لوسع $u (t)$ و $U_{m i n}$ قيمة وسعه الدنوية

$2$ نضبط الخط الضوئي الأفقي ليكون وسط شاشة راسم التذبذب قبل تطبيق أي توتر. نعاين التوتر $u (t)$ فنحصل على الرسم التذبذبي الممثل في الشكل $5$

الحساسية الأفقية: $20 μ S . d i v^{- 1}$

الحساسية الرأسية: $1 V . d i v^{- 1}$ . حدد $f_{p}$ و $f_{s}$ و $m$

ماذا تستنتج بخصوص جودة التضمين ؟

الكهرباء

الجزء الأول: دراسة ثنائي القطب $R C$ والدارة $L C$

$1$ دراسة ثنائي القطب $R C$

$1 - 1$ تعبير السعة $C_{e}$

المكثفين مركبين على التوالي وبالتالي لهما نفس الشحنة

حسب قانون إضافية التوترات $u_{A B} = u_{A D} + u_{D B}$

مع $u_{A B} = \frac{q}{C_{e}}$ و $u_{A D} = \frac{q}{C_{1}}$ و $u_{D B} = \frac{q}{C_{2}}$

ومنه $\frac{q}{C_{e}} = \frac{q}{C_{1}} + \frac{q}{C_{2}}$ أي $\frac{1}{C_{e}} = \frac{C_{1} + C_{2}}{C_{1} . C_{2}}$

نستنتج التعبير:

$C_{e} = \frac{C_{1} . C_{2}}{C_{1} + C_{2}}$

$2 - 1$ حسب قانون إضافية التوترات $u_{1} (t) + u_{2} (t) + u_{R} (t) = E$

$u_{1} + u_{2} + u_{R} = E \Rightarrow \frac{C_{2}}{C_{1}} . u_{2} + u_{2} + R . C_{2} \frac{d u_{2}}{d t} = E \Rightarrow u_{2} (1 + \frac{C_{2}}{C_{1}}) + R . C_{2} \frac{d u_{2}}{d t} = E \Rightarrow u_{2} \frac{C_{2}}{C_{e}} + R . C_{2} \frac{d u_{2}}{d t} = E$

المعادلة التفاضلية تكتب

$\frac{d u_{2} (t)}{d t} + \frac{1}{R . C_{e}} . u_{2} (t) = \frac{E}{R . C_{2}}$

$3 - 1$ تعبير الثابتين $A$ و $α$

حل المعادلة التفاضلية $u_{2} (t) = A . (1 - e^{- α t})$ ومنه فإن $\frac{d u_{2}}{d t} = A . α . e^{- α t}$

نعوض في المعادلة التفاضلية

$A . α . e^{- α t} + \frac{1}{R . C_{e}} A (1 - e^{- α t}) = \frac{E}{R . C_{2}} \Rightarrow A . α . e^{- α t} (α - \frac{1}{R . C_{e}}) + \frac{1}{R . C_{e}} . A - \frac{E}{R . C_{2}} = 0 \Rightarrow \{\begin{cases} α - \frac{1}{R . C_{e}} = 0 \\ \frac{1}{R . C_{e}} . A - \frac{E}{R . C_{2}} = 0 \end{cases} \Rightarrow \{\begin{cases} α = \frac{1}{R . C_{e}} \\ A = \frac{C_{e}}{C_{2}} . E \end{cases} \Rightarrow \{\begin{cases} α = \frac{C_{1} + C_{2}}{R . C_{1} . C_{2}} \\ A = \frac{C_{1}}{C_{2} + C_{1}} . E \end{cases}$

$1 - 4 - 1$ تحديد قيمة:

$E أ$

مبيانيا عند اللحظة $t = 0$ لدينا $u_{R} (0) = 12 V$ و $u_{2} (0) = 0$ و $u_{1} (0) = \frac{C_{2}}{C_{1}} . u_{2} (0) = 0$

حسب قانون إضافية التوترات $u_{1} (0) + u_{2} (0) + u_{R} (0) = E$

أي

$E = u_{R} (0) = 12 V$

$ب$ كل من $u_{2} (t)$ و $u_{1} (t)$ في النظام الدائم

مبيانيا حسب الشكل $2$ نجد $u_{2} = 8 V$

لحساب $u_{2}$ نستعمل قانون إضافية التوترات $u_{1} = E - u_{2} - u_{R} = 12 - 8 - 0 = 4 V$

$2 - 4 - 1$ التوصل الى قيمة $C_{1}$

في النظام الدائم العلاقة تكتب

$C_{1} . u_{1} = C_{2} . u_{2} \Rightarrow C_{1} = \frac{u_{2}}{u_{1}} C_{2} A . N : C_{1} = \frac{8}{4} 2 = 4 μ F$

$2$ دراسة التذبذبات الكهربائية في الدارة $L C$

$1 - 2$ التوصل الى المعادلة التفاضلية

لدينا

$u_{L} = L \frac{d i}{d t} = L \frac{d}{d t} \frac{d q}{d t} = L \frac{d}{d t} \frac{d (C_{2} . u_{2})}{d t} = L . C_{2} . \frac{d^{2} u_{2}}{d t^{2}}$

حسب قانون إضافية التوترات $u_{L} + u_{2} = 0$

أي

$L . C_{2} . \frac{d^{2} u_{2} (t)}{d t^{2}} + u_{2} (t) = 0 \Rightarrow \frac{d^{2} u_{2} (t)}{d t^{2}} + \frac{1}{L . C_{2}} u_{2} (t) = 0 \Rightarrow \frac{d^{2} u_{L} (t)}{d t^{2}} + \frac{1}{L . C_{2}} u_{L} (t) = 0$

$2 - 2$

$1 - 2 - 2$ تحديد الطاقة الكلية للدارة

$E_{T} = E_{e} + E_{m} E_{T} = E_{e_{m a x}} = E_{m_{m a x}} E_{T} = \frac{1}{2} C_{2} . {u_{2_{m a x}}}^{2} E_{T} = \frac{1}{2} C_{2} . {u_{L_{m a x}}}^{2}$

مبيانيا نجد $u_{L_{m a x}} = - u_{2_{m a x}} = - 8 V$

ت.ع:

$E_{T} = \frac{1}{2} \times 2 . 10^{- 6} \times {(- 8)}^{2} = 6, 4 . 10^{- 5} J$

$2 - 2 - 2$ حساب الطاقة المغناطيسية عند اللحظة $t = 2, 7 m s$

عند اللحظة $t = 2, 7 m s$ نجد مبيانيا $u_{L} = 4 V$

$E_{T} = E_{e} + E_{m} \Rightarrow E_{m} = E_{T} - E_{e} \Rightarrow E_{m} = E_{T} - \frac{1}{2} C_{2} . {(u_{L_{m a x}})}^{2}$

ت.ع:

$E_{m} = 6, 4 . 10^{- 5} - \frac{1}{2} \times 2 . 10^{- 6} \times {(- 4, 1)}^{2} \approx 4, 1 . 10^{- 5} J$

الجزء الثاني: دراسة جودة تضمين الوسع

$1$ إيجاد تعبير نسبة التضمين $m$

تعبير التوتر المضمن:

$u (t) = A [\frac{m}{S_{m}} s (t) + 1] . \cos (2 {πf}_{p} t) u (t) = A [\frac{m}{S_{m}} S_{m} \cos (2 {πf}_{s} t) + 1] . \cos (2 {πf}_{p} t) u (t) = A [m . \cos (2 {πf}_{s} t) + 1] . \cos (2 {πf}_{p} t) u (t) = U_{m} (t) . \cos (2 {πf}_{p} t)$

وسع التوتر المضمن $U_{m} (t) = A [m . \cos (2 {πf}_{s} t) + 1]$ يتراوح بين قيمتين حديتين: قيمة قصوية $U_{m a x}$ وقيمة دنوية $U_{m i n}$ حيث

$\{\begin{cases} U_{m a x} = A . (m + 1) \\ U_{m i n} = A . (- m + 1) \end{cases} \Rightarrow \frac{U_{m a x}}{U_{m i n}} = \frac{A . (m + 1)}{A . (- m + 1)} \Rightarrow - m . U_{m a x} + U_{m a x} = m . U_{m i n} + U_{m i n} \Rightarrow m = \frac{U_{m a x} - U_{m i n}}{U_{m a x} + U_{m i n}}$

$2$ تحديد $f_{p}$ و $f_{s}$

ليكن $T_{s}$ دور التوتر المضمن حسب الشكل $5$

$f_{s} = \frac{1}{T_{s}} = \frac{1}{5 d i v \times 20 μ s . d i v^{- 1}} = 10 K H z$

ليكن $T_{p}$ دور التوتر المضمن حسب الشكل $5$

$T_{s} = 16 T_{p} \Rightarrow f_{p} = 16 f_{s} = 160 K H z$

تحديد نسبة التضمين:

حسب الشكل $5$ :

$\{\begin{cases} U_{m a x} = 3 V \\ U_{m i n} = 1 V \end{cases} \Rightarrow m = \frac{U_{m a x} - U_{m i n}}{U_{m a x} + U_{m i n}} = 0, 5$

استنتاج:

التضمين جيد لأن

$\{\begin{cases} m = 0, 5 < 1 \\ f_{p} = 16 . f_{s} \geq 10 . f_{s} \end{cases}$
4

التمرين 4

الميكانيك

(الجزءآن الأول والثاني مستقلان)

الجزء الأول: دراسة تأثير مجال كهرساكن منتظم ومجال مغنطيسي منتظم على حزمة إلكترونات

درس العالم الانجليزي ج.ج.طومسون $(J . J . T h o m s o n)$ تأثير مجال كهرساكن منتظم ومجال مغنطيسي منتظم على حزمة إلكترونات تتحرك بنفس السرعة $\vec{V_{0}}$ وذلك لتحديد الشحنة الكتلية $\frac{e}{m}$ للإلكترون مع $m$ كتلة الإلكترون و $e$ الشحنة الابتدائية

يهدف هذا الجزء الى تحديد هذه النسبة اعتمادا على تجربتين

نعتبر أن حركة الإلكترون تتم في الفراغ وأن تأثير وزنه على هذه الحركة مهمل

$1$ التجربة الأولى

ينتج مدفع إلكترونات حزمة إلكترونات. تصل هذه الحزمة الى النقطة $O$ بالسرعة $\vec{V_{0}} = V_{0} \vec{i}$ فتخضع، أثناء حركتها طول المسافة $d$ ، الى تأثير مجال كهرساكن منتظم $\vec{E}$ محدث بواسطة صفيحتين فلزيتين $(P)$ و $(P')$ متعامدتين مع المستوى $(x O y)$ وتفصل بينهما المسافة $l$ (الشكل $1$ )

نرمز بـ $U$ لفرق الجهد بين $(P)$ و $(P')$ بحيث $U = V_{p} - V_{p'}$ وبـ $D$ للمسافة الفاصلة بين النقطة $I$ والشاشة المستشععة

ندرس حركة إلكترون من هذه الحزمة في المعلم المتعامد والممنظم $R (O, \vec{i}, \vec{j}, \vec{k})$ المرتبط بمرجع أرضي نعتبره غاليليا

نعتبر اللحظة التي يمر فيها الإلكترون من النقطة $O$ أصلا للتواريخ $(t = 0)$

$1 - 1$ بين أن معادلة مسار الإلكترون في المعلم $R (O, \vec{i}, \vec{j}, \vec{k})$ تكتب: $y = \frac{e U}{2 l m {V_{0}}^{2}} x^{2}$

$2 - 1$ تخرج حزمة الإلكترونات من المجال الكهرساكن عند نقطة $S$ فتواصل حركتها لتصطدم بالشاشة عند النقطة $M$

يمثل المستقيم $T$ المماس للمسار عند النقطة $S$ (الشكل $1$ )

بين أن الانحراف الكهربائي $O' M$ لإلكترون يكتب: $O' M = \frac{e D d U}{l m {V_{0}}^{2}}$

$2$ التجربة الثانية

عند وصولها الى النقطة $O$ بالسرعة $\vec{V_{0}} = V_{0} \vec{i}$ تخضع حزمة الإلكترونات بالإضافة الى المجال الكهرساكن السابق الى مجال مغنطيسي $\vec{B}$ منتظم ومتعامد مع $\vec{E}$

نضبط شدة المجال المغنطيسي على القيمة $B = 1, 01 m T$ فتصطدم الإلكترونات بالشاشة عند النقطة $O'$ (الشكل $1$ )

$1 - 2$ حدد منحى متجهة المجال المغنطيسي $\vec{B}$

$2 - 2$ عبر عن سرعة الإلكترونات بدلالة $E$ و $B$

$3$ استنتج تعبير $\frac{e}{m}$ بدلالة $B$ و $U$ و $D$ و $l$ و $d$ و $O' M$ . احسب قيمة $\frac{e}{m}$ علما أن:

$\begin{matrix} O' M = 5, 4 c m \\ D = 30 c m \\ U = 1200 V \\ l = 2 c m \\ d = 6 c m \end{matrix}$

الجزء الثاني: دراسة حركة نواس مرن

يتكون متذبذب ميكانيكي رأسي من جسم صلب $S$ كتلته $m = 200 g$ ونابض لفاته غير متصلة وكتلته مهملة وصلابته $K$

ثبت أحد طرفي النابض بحامل ثابت بينما ثبت الطرف الاخر بالجسم $S$ (الشكل $2$ )

ندرس حركة مركز القصور $G$ للجسم $S$ في معلم $R (O, \vec{k})$ مرتبط بمرجع أرضي نعتبره غاليليا

نمعلم موضع $G$ عند لحظة $t$ بالأنسوب $z$ على المحور $(O, \vec{k})$

عند التوازن، ينطبق $G$ مع الأصل $O$ للمعلم $R (O, \vec{k})$ (الشكل $2$ )

نأخذ $π^{2} = 10$

$1$ الاحتكاكات مهملة

نزيح الجسم $S$ عن موضع توازنه رأسيا ثم نرسله عند لحظة نختارها أصلا للتواريخ $(t = 0)$ بسرعة بدئية $\vec{V_{0}} = V_{0 z} \vec{k}$

يمثل منحنى الشكل $3$ تطور الأنسوب $z (t)$ لمركز القصور $G$ خلال الزمن

$1 - 1$ حدد عند التوازن، تعبير الإطالة $Δ l_{0}$ للنابض بدلالة $m$ و $K$ و $g$ شدة الثقالة

$2 - 1$ أثبت المعادلة التفاضلية التي يحققها الأنسوب $z$ لمركز القصور G

$3 - 1$ يكتب حل هذه المعادلة التفاضلية على شكل $z = z_{m} \cos (\frac{2 π}{T_{0}} t + φ)$ حيث $T_{0}$ الدور الخاص للمتذبذب

حدد قيمة كل من $K$ و $V_{0 z}$

$2$ الاحتكاكات غير مهملة

ننجز تجربتين حيث في كل تجربة نغمر المتذبذب الميكانيكي في سائل معين.نزيح الجسم $S$ رأسيا عن موضع توازنه بمسافة $z_{0}$ ثم نحرره بدون سرعة بدئية عند اللحظة $t = 0$ ، فتتم حركة $S$ داخل السائل

يمثل المنحنيان $(1)$ و $(2)$ تطور الأنسوب $z$ لمركز القصور $G$ خلال الزمن في كل سائل على حدة (الشكل $4$ )

$1 - 2$ أقرن كل منحنى بنظام الخمود المناسب له

$2 - 2$ نختار المستوى الأفقي الذي تنتمي إليه النقطة $O$ ، أصل المعلم $R (O, \vec{k})$ ، مرجعا لطاقة الوضع الثقالية $(E_{p p} = 0) E_{p p}$ والحالة التي يكون فيها النابض غير مشوه مرجعا لطاقة الوضع المرنة $(E_{p e} = 0) E_{p e}$

بالنسبة للتذبذبات الموافقة للمنحنى $(1)$ :

$1 - 2 - 2$ أوجد عند لحظة $t$ تعبير طاقة الوضع $E_{p} = E_{p p} + E_{p e}$ بدلالة $K$ و $z$ و $Δ l'_{0}$ إطالة النابض عند التوازن داخل السائل

$2 - 2 - 2$ احسب تغير الطاقة الميكانيكية للمتذبذب بين اللحظتين $t_{1} = 0$ و $t_{2} = 0, 4 s$

الميكانيك

(الجزءآن الأول والثاني مستقلان)

الجزء الأول: دراسة تأثير مجال كهرساكن منتظم ومجال مغنطيسي منتظم على حزمة إلكترونات

$1$ التجربة الأولى

$1 - 1$ التوصل الى معادلة المسار

المجموعة المدروسة: {الالكترون}

جرد القوى: (بعد إهمال وزن الالكترون أمام شدة القوة الكهرساكنة)

$\vec{F}$ : القوة الكهرساكنة

نعتبر المرجع الأرضي مرجعا غاليليا, نطبق القانون الثاني لنيوتن: $\vec{F} = m . \vec{a}$

متجهة التسارع: $\vec{a} = \frac{\vec{F}}{m} = \frac{q}{m} \vec{E}$

نسقط العلاقة في المعلم $R (O, \vec{i}, \vec{j}, \vec{k})$

حسب الشروط البدئية: $\vec{O M_{0}} (\begin{matrix} 0 \\ 0 \\ 0 \end{matrix})$ و $\vec{V_{0}} (\begin{matrix} V_{0} \\ 0 \\ 0 \end{matrix})$

متجهة التسارع $\vec{a}$ ومتجهة السرعة $\vec{V}$ ومتجهة الموضع $\vec{O M}$

$\vec{a} (\begin{matrix} a_{x} = 0 \\ a_{y} = - \frac{q}{m} E \\ a_{z = 0} \end{matrix}) \overset{(ل م ا ك ت)}{\to} \vec{V} (\begin{matrix} V_{x} = V_{0} \\ V_{y} = - \frac{q}{m} E t \\ V_{z = 0} \end{matrix}) \overset{(ل م ا ك ت)}{\to} \vec{O M} (\begin{matrix} x = V_{0} t \\ y = - \frac{q}{2 m} E t^{2} \\ z = 0 \end{matrix})$

لدينا $q = - e$ و $E = \frac{U}{l}$

بإقصاء الزمن من المعادلتين الزمنيتين نحصل على معادلة المسار

$\{\begin{cases} x = V_{0} t \\ y = - \frac{q}{2 m} E t^{2} \end{cases} \Rightarrow y = \frac{e . U}{2 l m {V_{0}}^{2}} . x^{2}$

$2 - 1$ التوصل الى تعبير $O' M$

عند النقطة $S$ نقطة مغادرة الحزمة المجال الكهرساكن: حيث $x_{s} = d$ و $d = V_{0} . t_{s}$ أي $t_{s} = \frac{d}{V_{0}}$

متجهة السرعة عند النقطة $S$ (انظر الشكل $1$ ) تكتب

$\vec{V_{s}} \{\begin{cases} V_{s x} = V_{0} \\ V_{s y} = \frac{e . U}{m l} . t_{s} = \frac{e . U . d}{m l V_{0}} \end{cases} \Rightarrow \tan α = \frac{V_{s y}}{V_{s x}} = \frac{e . U . d}{m l {V_{0}}^{2}}$

الانحراف الكهربائي $D_{e}$ يمثل المسافة بين النقطة $O'$ نقطة الاصطدام في غياب المجال الكهرساكن والنقطة $M$ بوجوده

$\tan α = \frac{D_{e}}{D} = \frac{e . U . d}{m l {V_{0}}^{2}} \Rightarrow O' M = D_{e} = \frac{e . U . d . D}{m l {V_{0}}^{2}}$

$2$ التجربة الثانية

$1 - 2$ تحديد منحى متجهة المجال المغنطيسي $\vec{B}$

لكي تكون للحزمة الإلكترونية حركة مستقيمية منتظمة يجب أن تكون القوتين $\vec{F_{e}}$ و $\vec{F_{m}}$ متقابلتين

أي $\vec{F_{m}} = - \vec{F_{e}} = - F_{m} \vec{j}$

$\vec{B}$ عمودية على المتجهتين $\vec{V_{0}} = V_{0} \vec{i}$ و $\vec{F_{m}} = - F_{m} \vec{j}$ إذن $\vec{B} = \pm B \vec{k}$

باستعمال قاعدة الأصابع الثلاث لليد اليمنى يتم تحديد منحى $\vec{B}$ : نحصل على $\vec{B} = - B \vec{k}$

$2 - 2$ التعبير عن سرعة الإلكترونات $V_{0}$ بدلالة $E$ و $B$

يخضع الإلكترون لقوتين $\vec{F_{e}}$ و $\vec{F_{m}}$ متقابلتين: $\vec{F_{m}} + \vec{F_{e}} = \vec{0}$

$\{\begin{cases} \vec{F_{m}} = q \vec{V_{0}} \land \vec{B} \\ \vec{F_{e}} = q \vec{E} \end{cases} \Rightarrow \{\begin{cases} F_{m} = q . V_{0} . B \\ F_{e} = e . E \end{cases} \Rightarrow q . V_{0} . B = e . E \Rightarrow V_{0} = \frac{E}{B}$

$3$ تعبير $\frac{e}{m}$

$\{\begin{cases} O' M = \frac{e . U . d . D}{m l {V_{0}}^{2}} \\ V_{0} = \frac{E}{B} \end{cases} \Rightarrow O' M = \frac{e . U . d . D . B^{2}}{m . l . E^{2}} \Rightarrow \frac{e}{m} = \frac{O' M . l . E^{2}}{U . d . D . B^{2}} \Rightarrow \frac{e}{m} = \frac{O' M . U}{l . d . D . B^{2}} (E = \frac{U}{l})$

ت.ع: $\frac{e}{m} = \frac{5, 4 . 10^{- 2} \times 1200}{6 . 10^{- 2} \times 30 . 10^{- 2} \times 2 . 10^{- 2} \times {(1, 01 . 10^{- 3})}^{2}} = 1, 76 . 10^{11} C . K g^{- 1}$

الجزء الثاني: دراسة حركة نواس مرن

$1$ الاحتكاكات مهملة

$1 - 1$ تعبير الإطالة $Δ l_{0}$ عند التوازن

المجموعة المدروسة: الجسم $(S)$

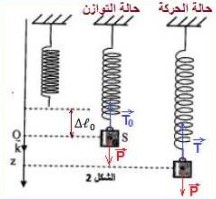
يخضع الجسم عند التوازن الى قوتين (انظر الشكل $2$ )

$\vec{P}$ : وزنه

$\vec{T_{0}}$ : توتر النابض

حسب مبدأ القصور $\vec{T_{0}} + \vec{P} = \vec{0}$ أي $P = T_{0}$ ومنه $m . g = K . Δ l_{0}$

إذن

$Δ l_{0} = \frac{m . g}{K}$

$2 - 1$ إثبات المعادلة التفاضلية التي يحققها الأنسوب $z$ لمركز القصور $G$

يخضع الجسم أثناء حركته الى قوتين (انظر الشكل $2$ )

$\vec{P}$ : وزنه

$\vec{T}$ : توتر النابض

نعتبر المعلم المرتبط بالأرض معلما غاليليا و نطبق القانون الثاني لنيوتن: $\vec{P} + \vec{T} = m . \vec{a_{G}}$

الإسقاط على المحور $O z$ يعطي

$P_{z} + T_{z} = m . a_{z} \Rightarrow m g - K (Δ l_{0} + z) = m . a_{z} \Rightarrow m g - K Δ l_{0} - K z = m . \ddot{z} \Rightarrow - K z = m . \ddot{z} (m . g = K . Δ l_{0}) \Rightarrow \ddot{z} + \frac{K}{m} . z = 0$

$3 - 1$ تحديد قيمة $K$

حسب تعبير الدور الخاص $T_{0}$ لدينا

$T_{0} = 2 π \sqrt{\frac{m}{K}} \Rightarrow {T_{0}}^{2} = 4 π^{2} \frac{m}{K} \Rightarrow K = 4 π^{2} \frac{m}{{T_{0}}^{2}}$

مبيانيا الدور الخاص هو $T_{0} = 0, 4 s$

إذن $K = 4 \times 10 \times \frac{0, 2}{0, 4^{2}} = 50 N . m^{- 1}$

تحديد $V_{0 z}$

حسب حل المعادلة التفاضلية: $z = z_{0} \cos (\frac{2 π}{T_{0}} . t + φ)$

الاشتقاق يعطي $V_{z} = - \frac{2 π}{T_{0}} z_{0} \sin (\frac{2 π}{T_{0}} . t + φ)$

عند $t = 0$ السرعة هي $V_{0 z} = - \frac{2 π}{T_{0}} z_{0} \sin φ$

حسب الشكل $3$ لدينا $z_{0} = 4 c m$

عند $t = 0$ لدينا $z (0) = z_{0} \cos φ$

$\{\begin{cases} z (0) = z_{0} \cos φ \\ z (0) = \frac{z_{0}}{2} \end{cases} \Rightarrow \cos φ = \frac{1}{2} \Rightarrow φ = \pm \frac{π}{3}$

$V_{0 z} = - \frac{2 π}{T_{0}} z_{0} \sin φ < 0 \Rightarrow φ = \frac{π}{3} \Rightarrow V_{0 z} = - \frac{2 π}{0, 4} \times 4 . 10^{- 2} \times \sin \frac{π}{3} \Rightarrow V_{0 z} = - 0, 54 m . s^{- 1}$

$2$ الاحتكاكات غير مهملة

$1 - 2$ إقران المنحنى بنظام الخمود

المنحنى (1) يوافق النظام شبه دوري

المنحنى (2) يوافق النظام لا دوري

$2 - 2$

$1 - 2 - 2$ تعبير طاقة الوضع $E_{p}$

طاقة الوضع تساوي مجموع طاقة الوضع الثقالية $(E_{p p} = - m g z + C)$ وطاقة الوضع المرنة $(E_{p e} = \frac{1}{2} K . {(Δ l_{0} + z)}^{2} + C')$

نختار المستواة الافقي المار من أصل المعلم مرجعا لطاقة الوضع الثقالية: $E_{p p_{0}} = 0 \Rightarrow C = 0$ إذن $E_{p p} = - m g z$

نختار الحالة التي يكون فيها النابض غير مشوه مرجعا لطاقة الوضع المرنة: $E_{p e} (z = - Δ l_{0}) = 0 \Rightarrow C' = 0$ إذن $E_{p e} = \frac{1}{2} K . {(Δ l_{0} + z)}^{2}$

تعبير طاقة الوضع هو

$E_{p} = E_{p p} + E_{p e} E_{p} = - m g z + \frac{1}{2} K . {(Δ l_{0} + z)}^{2} E_{p} = - m g z + \frac{1}{2} K . Δ {l_{0}}^{2} + K . Δ l_{0} . z + \frac{1}{2} K . z^{2}$

بما أن $m g = K . Δ l_{0}$ فإن

$E_{p} = - K . Δ l_{0} . z + \frac{1}{2} K . Δ {l_{0}}^{2} + K . Δ l_{0} . z + \frac{1}{2} K . z^{2} E_{p} = \frac{1}{2} K . (z^{2} + Δ {l_{0}}^{2})$

ملحوظة: منحى $O z$ نحو الأسفل لذلك تعير طاقة الوضع الثقالية هو $E_{p p} = - m g z$

$2 - 2 - 2$ حساب تغير الطاقة الميكانيكية للمتذبذب بين اللحظتين $t_{1} = 0$ و $t_{2} = 0, 4 s$

$Δ E_{m} = Δ E_{p p} + Δ E_{c}$

عندما تكون طاقة الوضع قصوية تكون الطاقة الحركية منعدمة والعكس صحيح

عند اللحظة $t_{1} = 0$ لدينا $z (0) = 3 c m$ و $V_{z} (0) = 0$

عند اللحظة $t_{2} = 0, 4 s$ لدينا $z (t_{2}) = 3 c m$ و $V_{z} (t_{2}) = 0$

إذن

$Δ E_{m} = Δ E_{p p} + Δ E_{c} Δ E_{m} = E_{p p 2} - E_{p p 1} + E_{c 2} - E_{c 1} Δ E_{m} = \frac{1}{2} K [z^{2} (t_{2}) + Δ {l_{0}}^{2}] - \frac{1}{2} K [z^{2} (t_{1}) + Δ {l_{0}}^{2}] Δ E_{m} = \frac{1}{2} K [z^{2} (t_{2}) - z^{2} (t_{1})]$

ت.ع: $Δ E_{m} = 0, 5 \times 50 \times [{(2, 2 . 10^{- 2})}^{2} - {(3 . 10^{- 2})}^{2}] = 1, 04 . 10^{- 2} J$