مسألة: دراسة دالة عددية وحساب التكامل
لدينا
إذن
لدينا
إذن المستقيم الذي معادلته مقارب للمنحنى بجوار
لدينا
إذن
لدينا
هندسيا يقبل فرعا شلجميا في إتجاه محور الأراتيب بجوار
لیكن من
لدينا
ولدينا
جدول التغیرات:
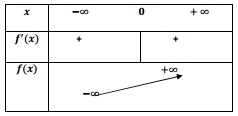
الدالة متصلة وتزايدية قطعا على
إذن المعادلة تقبل حلا وحيدا في حسب مبرهنة القيم الوسطية
ومنه يوجد عدد حقيقي وحيد من المجال بحيث
لیكن من
لدينا
وبما أن فإن إشارة هي إشارة
ولدينا
إذن
وبالتالي يوجد فوق المستقيم على المجال
ولدينا
إذن يوجد تحت المستقيم على المجال
لدينا
ولدينا
و
بما أن تنعدم في مع تغير إشارتها فإن نقطة انعطاف
إنشاء
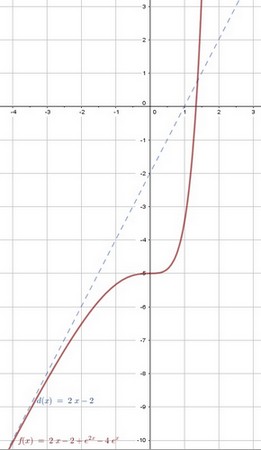
لدينا
المساحة هي:
المعادلة المميزة ب هي:
لدينا
إذن حلول هي الدوال المعرفة بما يلي:
ليكن حل المعادلة الذي يحقق الشرطين و
لدينا
الخلاصة:
الدالة قابلة للاشتقاق على
ولدينا
إذن الدالة قابلة للاشتقاق على ومشتقتها هي:
بما أن فإن و أي
ومنه تزايدية قطعا على
ولدينا متصلة على لأنها قابلة للاشتقاق عليه
إذن تقبل دالة عكسية معرفه على المجال بحيث
نضع
لدينا
الخلاصة:
لدينا
ولدينا
ولدينا أيضا
الخلاصة: