
Mathématiques : 1Bac SM
Séance 18-1 : Produit vectoriel dans l'espace (Cours)
Professeur : Mr CHEDDADI Haitam
Sommaire
I- Orientation de l'espace
1-1/ Trièdre
1-2/ Bonhomme d'ampère - Repère orienté de l'espace
II- Produit vectoriel de Deux vecteur
2-1/ Définition du produit vectoriel
2-2/ Interprétation géométrique du produit vectoriel
III- Propriétés du produit vectoriel
3-1/ Anti-symétrie du produit vectoriel
3-2/ Bilinéarité du produit vectoriel
3-3/ Expression analytique du produit vectoriel
IV- Applications du produit vectoriel
4-1/ Aire d'un triangle
4-2/ Équation d'un plan défini par trois points non alignés
4-3/ Intersection de deux plans de l'espace
4-4/ Distance d’un point à une droite
I- Orientation de l'espace
1-1/ Trièdre
Définition
Trois demi-droites , et de même origine O et non coplanaires déterminent, dans cet ordre un trièdre que l’on le note .
, et sont appelées les arêtes du trièdre

I- Orientation de l'espace
1-2/ Bonhomme d'ampère - Repère orienté de l'espace
Définition
Soit un repère de l'espace .
On pose : et et .
- On dit que le repère est direct lorsque le trièdre est direct.
- On dit que l’espace est orienté positivement lorsqu'il est muni d’un repère direct.
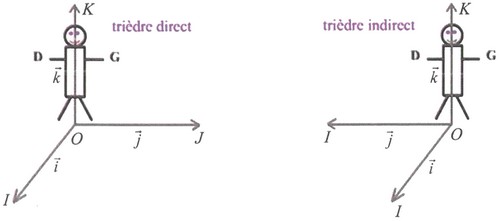
I- Orientation de l'espace
1-2/ Bonhomme d'ampère - Repère orienté de l'espace
Proposition
Si le repère est orthonormal direct, alors :
1) Les repères et sont directs.
2) Les repères , et sont indirects.
3) Les repères , et sont indirects.
Remarque
Soit un point quelconque de l’espace . Alors :
est un repère directLa base est directe.
II- Produit vectoriel de Deux vecteur
2-1/ Définition du produit vectoriel
Définition
Soit et deux vecteurs de l’espace orienté tels que et .
- Si et ne sont pas colinéaires, alors le produit vectoriel des vecteurs et , dans cet ordre, noté , est le vecteur défini par :
- la droite est perpendiculaire au plan ;
- le trièdre est direct ;
- où
- Si et sont colinéaires, alors :

II- Produit vectoriel de Deux vecteur
2-1/ Définition du produit vectoriel
Remarques
- Le produit vectoriel des vecteurs et ne dépend pas du choix du point .
- Le produit vectoriel de deux vecteurs est un vecteur, tandis que le produit scalaire de deux vecteurs est un réel.
- Si , alors et et .
- Si , alors la base est directe. En particulier, si les vecteurs et sont unitaires et orthogonaux, alors est une base orthonormée directe.
- Pour tout vecteur : et
- Les points , et de l'espace sont alignés si, et seulement si :
II- Produit vectoriel de Deux vecteur
2-1/ Définition du produit vectoriel
Applications
Soit et deux vecteurs de l’espace orienté tels que et et .
1)Calculer .
Soit et deux vecteurs de l’espace orienté tels que et et .
- Calculer .
II- Produit vectoriel de Deux vecteur
2-2/ Interprétation géométrique du produit vectoriel
Soit et deux vecteurs de l'espace orienté tels que et et .
Le réel est l'aire du parallélogramme construit sur les représentants et des vecteurs et .
En effet :
Et l'aire du parallélogramme est :

III- Propriétés du produit vectoriel
3-1/ Anti-symétrie du produit vectoriel
Proposition
Pour tous vecteurs et de l’espace orienté, on a :
On dit que le produit vectoriel est antisymétrique.
III- Propriétés du produit vectoriel
3-2/ Bilinéarité du produit vectoriel
Proposition
Soit , et trois vecteurs de l’espace orienté et un nombre réel.
Alors :
On dit que le produit vectoriel est bilinéaire.
III- Propriétés du produit vectoriel
3-3/ Expression analytique du produit vectoriel
Proposition
L'espace est rapporté à une base orthonormée directe .
Soit et deux vecteurs de l’espace .
Alors :
III- Propriétés du produit vectoriel
3-3/ Expression analytique du produit vectoriel
Applications
On considère les vecteurs :
- Déterminer, dans la base , les coordonnées de chacun des vecteurs et .
Dans l’espace rapporté à un repère orthonormé direct , on considère les points :
- Calculer et .
IV- Applications du produit vectoriel
4-1/ Aire d'un triangle
Proposition
Soit , et trois points non alignés de l’espace orienté .
L’aire du triangle est :
IV- Applications du produit vectoriel
4-1/ Aire d'un triangle
Applications
- Calculer l’aire du triangle dans chacun des cas suivants :
IV- Applications du produit vectoriel
4-2/ Équation d'un plan défini par trois points non alignés
Proposition
Soit , et trois points non alignés de l’espace orienté .
On a :
IV- Applications du produit vectoriel
4-2/ Équation d'un plan défini par trois points non alignés
Applications
On considère les deux points et .
- Déterminer une équation cartésienne du plan .
IV- Applications du produit vectoriel
4-3/ Intersection de deux plans de l'espace
Proposition
Soit et deux plans sécants suivant une droite dans l'espace orienté .
Si est un vecteur normal de et est un vecteur normal de , alors est un vecteur directeur de la droite d'intersection .

IV- Applications du produit vectoriel
4-3/ Intersection de deux plans de l'espace
Applications
- Déterminer l’intersection des plans et dans chacun des cas suivants :
IV- Applications du produit vectoriel
4-4/ Distance d’un point à une droite
Proposition
L'espace est rapporté à un repère orthonormé direct .
Soit la droite passant par et dirigée parle vecteur .
La distance d'un point de l’espace à la droite est donnée par :

IV- Applications du produit vectoriel
4-4/ Distance d’un point à une droite
Applications
- Calculer la distance du point à la droite dans chacun des cas suivants :


