Séance 11-2-1 : Dérivabilité d'une fonction numérique - Partie 2 (Cours)

Sommaire

V- Applications de la dérivation

5-1/ Monotonie d’une fonction numérique

5-2/ Extrema d'une fonction dérivable sur un intervalle

VI- Dérivées successives

VII- L'équation différentielle

V- Applications de la dérivation

5-1/ Monotonie d’une fonction numérique

Proposition

Soit $f$ une fonction dérivable sur un intervalle $I$ de $\mathrm{ℝ}$.

- Si la fonction $f$ est constante sur $I$, alors : $\left(\forall x\in I\right) f\text{'}\left(x\right)=0$

- Si la fonction $f$ est croissante sur $I$, alors : $\left(\forall x\in I\right) f\text{'}\left(x\right)\ge 0$

- Si la fonction $f$ est décroissante sur $I$, alors : $\left(\forall x\in I\right) f\text{'}\left(x\right)\le 0$

V- Applications de la dérivation

5-1/ Monotonie d’une fonction numérique

Proposition

Soit $f$ une fonction dérivable sur un intervalle $I$ de $\mathrm{ℝ}$.

- Si $f\text{'}$ est positive sur $I$ et ne s'y annule qu'en un nombre fini de points, alors la fonction $f$ est strictement croissante sur I.

- Si $f\text{'}$ est négative sur $I$ et ne s'y annule qu'en un nombre fini de points, alors la fonction $f$ est strictement décroissante sur /.

- Si $f\text{'}$ est nulle sur $I$, alors la fonction $f$ est constante sur $I$.

Remarques

- Les résultats de la proposition précédente ne sont valables que sur un intervalle.

- La fonction dérivée est un outil puissant pour étudier la monotonie d'une fonction numérique.

Pour étudier la monotonie d'une fonction $f$ dérivable sur un intervalle de $\mathrm{ℝ}$, on calcule la fonction dérivée $f\text{'}$ puis on détermine son signe et on utilise la proposition précédente.

V- Applications de la dérivation

5-1/ Monotonie d’une fonction numérique

Applications

1. En utilisant la fonction dérivée, étudier les variations de la fonction $f$ dans chacun des cas suivantes :

V- Applications de la dérivation

5-2/ Extrema d'une fonction dérivable sur un intervalle

Proposition

Soit $f$ une fonction dérivable sur un intervalle ouvert $I$ et $a$ un élément de $I$.

Si $f$ admet un extremum local au point $a$, alors : $f\text{'}\left(a\right)=0$

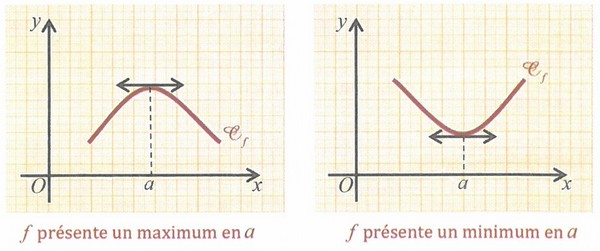
V- Applications de la dérivation

5-2/ Extrema d'une fonction dérivable sur un intervalle

Remarques

- La réciproque de la proposition précédente est évidemment fausse comme le montre l'exemple classique $f\left(x\right)=x^3$ sur $\mathrm{ℝ}$. Pour cet exemple, on a $f\text{'}\left(0\right)=0$ mais $f$ ne présente pas un extremum en $0$ :

La condition $f\text{'}\left(a\right)=0$ est donc nécessaire mais pas suffisante pour que la fonction $f$ présente un extremum un point $a$ d'un intervalle ouvert $I$.

- Si $f$ admet un extremum local au point $a$, alors la tangente à la courbe ${\mathcal{C}}_f$ au point $A\left(a;f\left(a\right)\right)$ est horizontale.

V- Applications de la dérivation

5-2/ Extrema d'une fonction dérivable sur un intervalle

Proposition

Soit $f$ une fonction dérivable sur un intervalle ouvert $I$ et $a$ un élément de $I$.

Si $f\text{'}$ s’annule en $a$ en changeant de signe, alors $f$ admet un extremum en $a$.

V- Applications de la dérivation

5-2/ Extrema d'une fonction dérivable sur un intervalle

Applications

1. Déterminer les extrema de chacune des fonctions suivantes :

$$\begin{gathered} \boxed{1} f\left(x\right)=4x^3-x^2-1 \\ \boxed{2} f\left(x\right)=\sqrt{x^2+2x-3} \\ \boxed{3} f\left(x\right)=\frac{x^2-4}{x^2+1} \end{gathered}$$

VI- Dérivées successives

Définition

Soit $f$ une fonction dérivable sur un intervalle $I$ de $\mathrm{ℝ}$.

On dit que la fonction $f$ est deux fois dérivable sur $I$ si $f$ est dérivable sur / et $f\text{'}$ dérivable sur $I$.

La dérivée de la fonction $I$ s'appelle la dérivée seconde de $f$ est notée $f"$.

Plus généralement, on définit par récurrence la dérivée $n^{ième}$ de la fonction $f$, notée $f^{\left(n\right)}$, comme suit :

- On pose : $f^{\left(0\right)}=f$

- Pour $n\ge 1$, on dit que $f$ est $n$ fois dérivable sur $I$ si elle est $n-1$ fois dérivable sur $I$ et si $f^{\left(n-1\right)}$ est dérivable sur $I$. On pose alors : $f^{\left(n\right)}={\left(f^{\left(n-1\right)}\right)}^{\text{'}}$.

VI- Dérivées successives

Applications

On considère la fonction $f$ définie sur $\mathrm{ℝ}-\left\{1\right\}$ par : $f\left(x\right)=\frac{1}{x-1}$

1. a- Calculer $f\text{'}\left(x\right)$ et $f"\left(x\right)$ pour tout $x\in \mathrm{ℝ}-\left\{1\right\}$

1. b- Montrer que : $\left(\forall x\in \mathrm{ℝ}-\left\{1\right\}\right) \left(\forall n\in \mathrm{\mathbb{N}}*\right) f^{\left(n\right)}\left(x\right)=\frac{{\left(-1\right)}^n.n!}{{\left(x-1\right)}^{n+1}}$

Soit $x\in \mathrm{ℝ}$.

2. Montrer par récurrence que : $\left(\forall n\in \mathrm{\mathbb{N}}*\right) {\sin }^{\left(n\right)}\left(x\right)=\sin \left(x+\frac{n\mathrm{\pi }}{2}\right)$

VII- L'équation différentielle

Définition

Soit $\omega$ un nombre réel non nul.

L'équation $y"+{\omega }^{2}y=0$ où l'inconnue est une fonction $y$ telle que $y"$ est sa dérivée seconde est appelée équation différentielle.

Toute fonction $f$ deux fois dérivable sur $\mathrm{ℝ}$ et vérifiant $f"\left(x\right)+{\omega }^{2}f\left(x\right)=0$ pour tout $x\in \mathrm{ℝ}$ est appelée solution de l'équation différentielle .

VII- L'équation différentielle

Proposition

Soit $\omega$ un nombre réel non nul.

La solution générale de l'équation différentielle $y"+{\omega }^{2}y=0$ est l'ensemble des fonctions $y$ définies sur $\mathrm{ℝ}$ par $y\left(x\right)=\alpha \cos \left(\omega x\right)+\beta \sin \left(\omega x\right)$ où $\left(\alpha ;\beta \right)\in {\mathrm{ℝ}}^2$.

VII- L'équation différentielle

Proposition

Soit $\omega$ un nombre réel non nul et $\left(x_0;y_0;y_1\right)\in {\mathrm{ℝ}}^3$.

Alors l'équation différentielle $y"+{\omega }^{2}y=0$ possède une solution unique $f$ vérifiant les conditions : $f\left(x_0\right)=y_0$ et $f\text{'}\left(x_0\right)=y_1$.

Remarques

- Dans le cas où $\omega =0$, l'équation différentielle $y"+{\omega }^{2}y=0$ devient $y"=0$. Dans ce cas, la solution générale de l'équation $y"=0$ est donnée par $y\left(x\right)=ax+b$ où $\left(a;b\right)\in {\mathrm{ℝ}}^2$.

- La solution générale de l'équation différentielle $y"+{\omega }^{2}y=0$ peut encore s'écrire sous la forme $y\left(x\right)=\lambda \cos \left(\omega x+\phi \right)$ ou $y\left(x\right)=\lambda \sin \left(\omega x+\phi \right)$ avec $\left(\lambda ;\phi \right)\in {\mathrm{ℝ}}^2$.

VII- L'équation différentielle

Applications

1. Résoudre les équations différentielles suivantes :

$$\begin{gathered} \boxed{1} y"+3y=0 \\ \boxed{2} y"+9y=0 \\ \boxed{3} y"+5y=0 \end{gathered}$$

2. Déterminer la solution $G$ de l'équation différentielle $y"+16y=0$ telle que $G\left(\frac{\mathrm{\pi }}{4}\right)=0$ et $G\text{'}\left(\frac{\mathrm{\pi }}{4}\right)=-1$.