Séance 10-2-1 : Limite d'une fonction numérique - Partie 2 (Cours)

Sommaire

VI- Opérations sur les limites

6-1/ Opérations sur les limites finies

6-2/ Limites finies et ordre

6-3/ Opérations sur les limites infinies

VII- Quelques méthodes pour lever une indétermination

7-1/ Limites d'une fonction polynôme ou rationnelle en $+\infty$ et $-\infty$

7-2/ Limites du type $\underset{x\to a}{\lim }\frac{f\left(x\right)}{g\left(x\right)}$ avec $f\left(a\right)=g\left(a\right)=0$

7-3/ Limites du type $\underset{x\to \pm \infty }{\lim }\left(\sqrt{a{x}^2+bx+c}+\alpha x+\beta \right)$

7-4/ Limites de fonctions trigonométriques

VI- Opérations sur les limites

6-1/ Opérations sur les limites finies

Proposition

Soit $f$ et $g$ deux fonctions numériques et $a\in \mathrm{ℝ}$.

Si $\underset{x\to a}{\lim }f\left(x\right)=\mathcal{l}$ et $\underset{x\to a}{\lim }g\left(x\right)=\mathcal{l}\text{'}$, alors :

- $\underset{x\to a}{\lim }\left(f+g\right)\left(x\right)=\mathcal{l}+\mathcal{l}\text{'} ; \underset{x\to a}{\lim }\left(f.g\right)\left(x\right)=\mathcal{ll}\text{'} ; \underset{x\to a}{\lim }\left|\left(f\right)\left(x\right)\right|=\left|\mathcal{l}\right|$

- Si $\mathcal{l}\text{'}\ne 0$ alors : $\underset{x\to a}{\lim }\left(\frac{1}{g}\right)\left(x\right)=\frac{1}{\mathcal{l}\text{'}}$ et $\underset{x\to a}{\lim }\left(\frac{f}{g}\right)\left(x\right)=\frac{\mathcal{l}}{\mathcal{l}\text{'}}$

- Si $k\in \mathrm{ℝ}$ alors : $\underset{x\to a}{\lim }\left(kf\right)\left(x\right)=k\mathcal{l}$

- Si $\mathcal{l}>0$ alors : $\underset{x\to a}{\lim }\sqrt{f\left(x\right)}=\sqrt{\mathcal{l}}$

Remarques

Ces propriétés restent aussi valables quand $x$ tend vers $a$ à droite ou à gauche ou $+\infty$ ou $-\infty$.

On peut démontrer ces propriétés en utilisant la définition de la limite finie en un point.

VI- Opérations sur les limites

6-1/ Opérations sur les limites finies

Applications

On considère la fonction $f:x\mapsto x^3+x^2+\frac{3x}{x+1}-2\sqrt{x^2-1}$.

1. Calculer $\underset{x\to 1^{+}}{\lim }f\left(x\right)$ et $\underset{x\to -2}{\lim }f\left(x\right)$.

2. Calculer les limites suivantes :

$$\begin{gathered} \boxed{1} \underset{x\to +\infty }{\lim }\left(2-\frac{1}{x}\right)\left(\frac{3}{\sqrt{x}}-1\right) \\ \boxed{2} \underset{x\to 1^{-}}{\lim }\left(\mathrm{\pi }-\frac{1}{x^3}\right)\left(\frac{1}{\mathrm{\pi }}+2x\right) \\ \boxed{3} \underset{x\to +\infty }{\lim }\frac{5{\mathrm{x}}^2-1}{3x^2+4} \\ \boxed{4} \underset{x\to \frac{\mathrm{\pi }}{4}}{\lim }\left(\frac{3x+\cos x}{2\sin x}+2x\tan x\right) \end{gathered}$$

VI- Opérations sur les limites

6-2/ Limites finies et ordre

Proposition

Soit $f$, $g$ et $h$ trois fonctions définies sur un ensemble de la forme $I=]a-r;a+r[-\left\{a\right\}$ où $a\in \mathrm{ℝ}$ et $r\in {\mathrm{ℝ}}_{+}^{*}$.

- Si $\underset{x\to a}{\lim }f\left(x\right)=\mathcal{l}$ et $f$ est positive sur $I$, alors : $\mathcal{l}\ge 0$

- Si $\underset{x\to a}{\lim }f\left(x\right)=\mathcal{l}$ et $\underset{x\to a}{\lim }g\left(x\right)=\mathcal{l}\text{'}$ et $f\le g$ sur $I$, alors : $\mathcal{l}\le \mathcal{l}\text{'}$

- Si $\underset{x\to a}{\lim }g\left(x\right)=\mathcal{l}$ et $\underset{x\to a}{\lim }h\left(x\right)=\mathcal{l}$ et $g\le f\le h$ sur $I$, alors : $\underset{x\to a}{\lim }f\left(x\right)=\mathcal{l}$

Remarque

Ces propriétés restent aussi valables quand $x$ tend vers $a$ à droite ou à gauche ou $+\infty$ ou $-\infty$.

VI- Opérations sur les limites

6-2/ Limites finies et ordre

Applications

On considère la fonction $f:x\mapsto \frac{x+1}{\sqrt{1+x^2}}$.

1. Montrer que pour tout $x\in {\mathrm{ℝ}}_{+}^{*}$ : $1\le f\left(x\right)\le 1+\frac{1}{x}$, puis en déduire la limite : $\underset{x\to +\infty }{\lim }f\left(x\right)$

2. Calculer les limites suivantes :

VI- Opérations sur les limites

6-3/ Opérations sur les limites infinies

Limite d'une somme de deux fonctions

VI- Opérations sur les limites

6-3/ Opérations sur les limites infinies

Limite d'un produit de deux fonctions

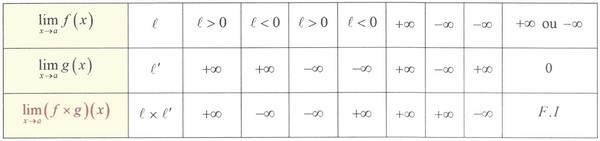
VI- Opérations sur les limites

6-3/ Opérations sur les limites infinies

Limite d’un quotient de deux fonctions

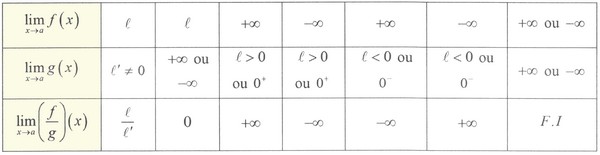
VI- Opérations sur les limites

6-3/ Opérations sur les limites infinies

Limite de l'inverse d’une fonction

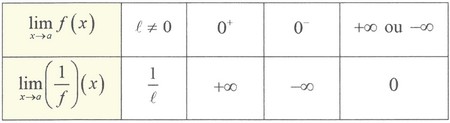
VI- Opérations sur les limites

6-3/ Opérations sur les limites infinies

Applications

1. Calculer les limites suivantes :

On considère la fonction $f$ définie sur $\mathrm{ℝ}-\left\{0;1\right\}$ par : $f\left(x\right)=\frac{2x+1}{x\left(x+1\right)}$

2. Calculer les limites suivantes :

$$\begin{gathered} \underset{x\to +\infty }{\lim }f\left(x\right) ; \underset{x\to -\infty }{\lim }f\left(x\right) \\ \underset{x\to 0^{+}}{\lim }f\left(x\right) ; \underset{x\to 0^{-}}{\lim }f\left(x\right) \\ \underset{x\to 1^{+}}{\lim }f\left(x\right) ; \underset{x\to 1^{-}}{\lim }f\left(x\right) ; \end{gathered}$$

VI- Opérations sur les limites

6-3/ Opérations sur les limites infinies

Remarques

L'obtention d'une forme indéterminée « F .I » signifie que la méthode mise en place pour calculer la limite de la fonction trébuche. Cela ne signifie en aucun cas que la fonction n'a pas de limite.

Des méthodes seront présentées au fur et à mesure, pour lever les indéterminations les plus classiques.

Parmi ces méthodes, on peut citer jusqu'à présent les techniques suivantes :

- Factoriser par le (les) terme(s) de plus haut degré si un terme est prépondérant.

- Factoriser par $x-a$ si $a$ est racine d'un polynôme $P$ : $P\left(x\right)=\left(x-a\right)P\text{'}\left(x\right)$

- Multiplier par l'expression conjuguée : $\left(x-\sqrt{y}\right)\left(x+\sqrt{y}\right)=x^2-y$

- Encadrement, majoration, minoration,

Les tableaux précédents donnent les résultats les plus classiques des limites rencontrées.

Voici trois conseils pour bien manipuler ces tableaux :

- Par exemple, on retiendra que diviser par $0^{+}$, c'est multiplier par $+\infty$ ;

- Il est souhaitable de comprendre ces tableaux au lieu de les apprendre par cœur.

- Une manière de lire ces tableaux est la suivante, mais attention NE JAMAIS L'ECRIRE SUR SA COPIE :

$$\begin{gathered} +\infty -\left(-\infty \right)=+\infty ; -\infty +\mathcal{l}=-\infty ; -\infty \times \left(-\infty \right)=+\infty \\ \frac{\mathcal{l}}{-\infty }=0 ; \frac{-1}{0^{+}}=-\infty ; \frac{+\infty }{0^{+}}=+\infty \end{gathered}$$

VII- Quelques méthodes pour lever une indétermination

7-1/ Limites d'une fonction polynôme ou rationnelle en $+\infty$ et $-\infty$

Proposition

Soit $P$ et $Q$ deux fonctions polynômes définies par :

$$\begin{gathered} P\left(x\right)=a_n{x}^n+a_{n-1}{x}^{n-1}+....+a_{1}x+a_0 \\ Q\left(x\right)=b_p{x}^p+b_{p-1}{x}^{p-1}+....+b_{1}x+b_0 \end{gathered}$$

où $a_n,...,a_1,a_0,b_p,...,b_1,b_0$ des réels tels que $a_n\ne 0$ et $b_p\ne 0$.

- La limite d’une fonction polynôme en $+\infty$ et $-\infty$ est la limite du monôme de plus haut degré :

$\underset{x\to +\infty }{\lim }P\left(x\right)=\underset{x\to +\infty }{\lim }{a}_n{x}^n$ et $\underset{x\to -\infty }{\lim }P\left(x\right)=\underset{x\to -\infty }{\lim }{a}_n{x}^n$

- La limite d’une fonction rationnelle $+\infty$ et $-\infty$ est la limite du quotient des monômes de plus haut degré :

$\underset{x\to +\infty }{\lim }\frac{P\left(x\right)}{Q\left(x\right)}=\underset{x\to +\infty }{\lim }\frac{a_n{x}^n}{b_p{x}^p}$ et $\underset{x\to -\infty }{\lim }\frac{P\left(x\right)}{Q\left(x\right)}=\underset{x\to -\infty }{\lim }\frac{a_n{x}^n}{b_p{x}^p}$

VII- Quelques méthodes pour lever une indétermination

7-1/ Limites d'une fonction polynôme ou rationnelle en $+\infty$ et $-\infty$

Applications

1. Calculer les limites suivantes :

VII- Quelques méthodes pour lever une indétermination

7-1/ Limites d'une fonction polynôme ou rationnelle en $+\infty$ et $-\infty$

Proposition

Soit $f$ une fonction définie et positive sur un intervalle de la forme $[A;+\infty [$ où $A\in \mathrm{ℝ}$.

Si $\underset{x\to +\infty }{\lim }f\left(x\right)=+\infty$, alors $\underset{x\to +\infty }{\lim }\sqrt{f\left(x\right)}=+\infty$.

Remarque

Ces propriétés restent aussi valables quand $x$ tend vers $-\infty$ ou vers $a$ à droite ou à gauche.

VII- Quelques méthodes pour lever une indétermination

7-2/ Limites du type $\underset{x\to a}{\lim }\frac{f\left(x\right)}{g\left(x\right)}$ avec $f\left(a\right)=g\left(a\right)=0$

Applications

1. Calculer les limites suivantes :

2. Calculer les limites suivantes :

VII- Quelques méthodes pour lever une indétermination

7-3/ Limites du type $\underset{x\to \pm \infty }{\lim }\left(\sqrt{a{x}^2+bx+c}+\alpha x+\beta \right)$

Applications

1. Calculer les limites suivantes :

$$\begin{gathered} \boxed{1} \underset{x\to +\infty }{\lim }\left(\sqrt{2x^2+1}-\sqrt{x^2-x-2}\right) \\ \boxed{2} \underset{x\to +\infty }{\lim }\left(\sqrt{x^3+3x^2+4}-x^2+2\right) \\ \boxed{3} \underset{x\to -\infty }{\lim }\left(\sqrt{3x^2-6x-1}+2x-5\right) \\ \boxed{4} \underset{\left|x\right|\to +\infty }{\lim }\left(\sqrt{x^2+x+1}-x-3\right) \\ \boxed{5} \underset{x\to -\infty }{\lim }\left(\sqrt{1-x^3}+x-1\right) \end{gathered}$$

2. Calculer suivant les valeurs du paramètre réel $m$, la limite suivante :

$\underset{x\to +\infty }{\lim }\left(\sqrt{x^2+x+1}+mx\right)$

Soit $a$, $b$ et $c$ trois réels non nuis tels que $a>0$.

3. Calculer suivant les valeurs de a la limite suivante :

$\underset{x\to -\infty }{\lim }\left(\sqrt{a{x}^2+bx+c}+x\right)$

VII- Quelques méthodes pour lever une indétermination

7-4/ Limites de fonctions trigonométriques

Proposition

Soit $a$un réel non nul.

On a :

$\underset{x\to 0}{\lim }\frac{\sin x}{x}=1 ; \underset{x\to 0}{\lim }\frac{\tan x}{x}=1 ; \underset{x\to 0}{\lim }\frac{\sin \left(ax\right)}{ax}=1$

$\underset{x\to 0}{\lim }\frac{\tan \left(ax\right)}{ax}=1 ; \underset{x\to 0}{\lim }\frac{1-\cos x}{x^2}=\frac{1}{2}$

VII- Quelques méthodes pour lever une indétermination

7-4/ Limites de fonctions trigonométriques

Applications

1. Calculer les limites suivantes :