Séance 9-1 : La rotation dans le plan (Cours)

Sommaire

I- Rotation - Rotation réciproque d’une rotation

1-1/ Rotation

1-2/ Rotation réciproque d'une rotation

1-3/ Décomposition d'une rotation

II- Propriétés des rotations

2-1/ Conservation de la distance

2-2/ Conservation des mesures des angles orientés

2-3/ Conservation du coefficient de colinéarité de deux vecteurs

2-4/ Conservation du barycentre

III- Images de certaines figures par une rotation

3-1/ Image d'un cercle par une rotation

3-2/ Image d'une droite, d'une demi-droite et d'un segment

IV- Composition de deux rotations

I- Rotation - Rotation réciproque d’une rotation

1-1/ Rotation

Définition

Dans le plan $\mathcal{P}$ orienté positivement, on considère un point $\Omega$ et un réel $\theta$.

La rotation de centre $\Omega$ et d'angle $\theta$ est la transformation du plan, qui à tout point $M$ du plan associe le point $M\text{'}$ défini par :

- Si $M=\Omega$, alors : $M\text{'}=\Omega$

- Si $M\ne \Omega$, alors : $\left\{\begin{array}{l}\Omega M=\Omega M\text{'}\\ \left(\overline{\overrightarrow{\Omega M};\overrightarrow{\Omega M\text{'}}}\right)\equiv \theta \left[2\mathrm{\pi }\right]\end{array}\right.$

On note cette transformation par $r\left(\Omega ;\theta \right)$, ou simplement $r$ lorsqu'il n'y a pas de confusion possible.

I- Rotation - Rotation réciproque d’une rotation

1-1/ Rotation

Remarque

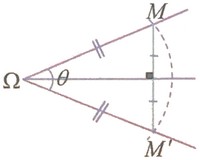
Si $\theta \ne 2k\mathrm{\pi } \left(\mathrm{k}\in \mathrm{\mathbb{Z}}\right)$ , alors $\Omega$ le centre de la rotation $r$ est l'unique point invariant par cette rotation, et dans ce cas : Pour tout point $M$ du plan tel que $M\ne \Omega$ et $r\left(M\right)=M\text{'}$, on a :

- Le point $M\text{'}$ appartient au cercle de centre $\Omega$ et de rayon $\Omega M$.

- La médiatrice du segment $\left[MM\text{'}\right]$ passe par le point $\Omega$.

- Le triangle $\Omega MM\text{'}$ est isocèle de sommet $\Omega$.

I- Rotation - Rotation réciproque d’une rotation

1-1/ Rotation

Applications

Soit $ABC$ un triangle équilatéral tel que : $\left(\overline{\overrightarrow{AB};\overrightarrow{AC}}\right)\equiv \frac{\mathrm{\pi }}{3} \left[2\mathrm{\pi }\right]$

1. Déterminer l'angle de la rotation de centre $B$ et qui transforme $A$ en $C$.

Soit $ABC$ un triangle équilatéral tel que $\left(\overline{\overrightarrow{AB};\overrightarrow{AC}}\right)\equiv \frac{\mathrm{\pi }}{3} \left[2\mathrm{\pi }\right]$, et $I$ le centre de gravité du triangle $ABC$.

On considère la rotation $r$ de centre $I$ et d'angle $\frac{2\mathrm{\pi }}{3}$.

2. a- Montrer que $r\left(A\right)=B$ et $r\left(B\right)=C$ et $r\left(C\right)=A$.

Soit $A\text{'}$ le milieu du segment $\left[BC\right]$.

2. b- Déterminer $r\left(A\text{'}\right)$.

Soit $ABCD$ un carré tel que : $\left(\overline{\overrightarrow{AB};\overrightarrow{AD}}\right)\equiv \frac{\mathrm{\pi }}{2} \left[2\mathrm{\pi }\right]$

On note $K$ et $L$ respectivement les milieux des segments $\left[CD\right]$ et $\left[AD\right]$.

3. Déterminer le centre et l'angle de la rotation r dans chacun des deux cas suivants :

$$\begin{gathered} \boxed{1} r\left(A\right)=B et r\left(B\right)=A \\ \boxed{2} r\left(A\right)=D et r\left(L\right)=K \end{gathered}$$

I- Rotation - Rotation réciproque d’une rotation

1-2/ Rotation réciproque d'une rotation

Proposition

Toute rotation $r\left(\Omega ;\theta \right)$ du plan $\mathcal{P}$ vers $\mathcal{P}$ est une application bijective.

Sa bijection réciproque est la rotation $r\left(\Omega ;-\theta \right)$, et on la note $r^{-1}$ ou $r^{-1}\left(\Omega ;\theta \right)=r\left(\Omega ;-\theta \right)$.

On a donc : Pour tous points $M$ et $N$ du plan :

$r\left(\Omega ;\theta \right)\left(M\right)=N\iff r\left(\Omega ;-\theta \right)\left(N\right)=M$

I- Rotation - Rotation réciproque d’une rotation

1-2/ Rotation réciproque d'une rotation

Applications

Soit $ABCD$ un carré de centre $O$ tel que : $\left(\overline{\overrightarrow{AD};\overrightarrow{AB}}\right)\equiv \frac{\mathrm{\pi }}{2} \left[2\mathrm{\pi }\right]$, et la rotation $r$ de centre $O$ et d'angle $\frac{\mathrm{\pi }}{2}$.

1. Déterminer $r\left(A\right)$, puis déduire $r^{-1}\left(D\right)$.

2. Déterminer $r^{-1}\left(C\right)$, puis déduire $r\left(D\right)$.

I- Rotation - Rotation réciproque d’une rotation

1-3/ Décomposition d'une rotation

Théorème

1) Si $\left(\Delta \right)$ et $\left(\Delta \text{'}\right)$ sont deux droites parallèles, alors $S_{\left(\Delta \text{'}\right)}\circ S_{\left(\Delta \right)}$ est la translation de vecteur $\overrightarrow{u}=\overrightarrow{AA\text{'}}$ où $A$ est un point de la droite $\left(\Delta \right)$ et $A\text{'}=S_{\left(\Delta \text{'}\right)}\left(A\right)$.

2) Toute translation $t$ de vecteur non nul $\overrightarrow{u}$ est décomposable en deux symétries orthogonales d'axes parallèles, dont l'un est choisi arbitrairement et l'autre est son image par la translation de vecteur $\frac{1}{2}\overrightarrow{u}$ ou $-\frac{1}{2}\overrightarrow{u}$.

3) Si $\left(\Delta \right)$ et $\left(\Delta \text{'}\right)$ sont deux droites sécantes en $\Omega$, alors $S_{\left(\Delta \text{'}\right)}\circ S_{\left(\Delta \right)}$ est la rotation de centre $\Omega$ et d'angle $\theta =2\left(\overline{\overrightarrow{u};\overrightarrow{u\text{'}}}\right)$ où $\overrightarrow{u}$ et $\overrightarrow{u\text{'}}$ sont respectivement deux vecteurs directeurs de $\left(\Delta \right)$ et $\left(\Delta \text{'}\right)$.

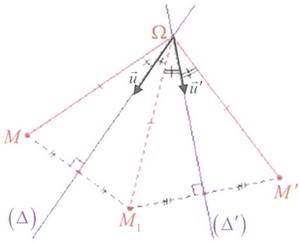
4) Toute rotation $r\left(\Omega ;\theta \right)$ peut s'exprimer comme composée de deux symétries orthogonales $S_{\left(\Delta \right)}$ et $S_{\left(\Delta \text{'}\right)}$ avec $\left(\Delta \right)$ et $\left(\Delta \text{'}\right)$ sont deux droites sécantes en $\Omega$.

Plus précisément : $r=S_{\left(\Delta \text{'}\right)}\circ S_{\left(\Delta \right)}$, avec $\left(\Delta \text{'}\right)\cap \left(\Delta \right)=\left\{\Omega \right\}$ et $\left(\overline{\overrightarrow{u};\overrightarrow{u\text{'}}}\right)\equiv \frac{\theta }{2} \left[2\mathrm{\pi }\right]$ où $\left(\Delta \right)=D\left(\Omega ;\overrightarrow{u}\right)$ et $\left(\Delta \text{'}\right)=D\left(\Omega ;\overrightarrow{u\text{'}}\right)$.

I- Rotation - Rotation réciproque d’une rotation

1-3/ Décomposition d'une rotation

Applications

Soit $ABC$ un triangle équilatéral de centre $O$ tel que : $\left(\overline{\overrightarrow{AB};\overrightarrow{AC}}\right)\equiv -\frac{\mathrm{\pi }}{3} \left[2\mathrm{\pi }\right]$

1. a- Déterminer une mesure de chacun des angles $\left(\overline{\overrightarrow{OB};\overrightarrow{OC}}\right)$ et $\left(\overline{\overrightarrow{OA};\overrightarrow{OB}}\right)$.

1. b- Déterminer puis tracer les droites $\left(\Delta \right)$, $\left(\Delta \text{'}\right)$, $\left({\Delta }_1\right)$ et $\left({\Delta }_2\right)$ telles que :

$r\left(O;-\frac{2\mathrm{\pi }}{3}\right)=S_{\left({\Delta }_1\right)}\circ S_{\left(OA\right)}=S_{\left({\Delta }_2\right)}\circ S_{\left(OB\right)}$

et

$r\left(A;\frac{\mathrm{\pi }}{3}\right)=S_{\left(\Delta \text{'}\right)}\circ S_{\left(AB\right)}=S_{\left(AC\right)}\circ S_{\left(\Delta \right)}$

2. a- Déterminer $S_{\left(\Delta \text{'}\right)}\circ S_{\left(\Delta \right)}$ lorsque $\left(\Delta \right)\perp \left(\Delta \text{'}\right)$.

Soit $\left(\Delta \right)$ et $\left(\Delta \text{'}\right)$ deux droites parallèles et $\left(D\right)$ une droite perpendiculaire à $\left(\Delta \right)$ et $\left(\Delta \text{'}\right)$.

2. b- Déterminer $S_{\left(D\right)}\circ S_{\left(\Delta \right)}$, $S_{\left(\Delta \text{'}\right)}\circ S_{\left(D\right)}$ et $\left(S_{\left(\Delta \text{'}\right)}\circ S_{\left(\Delta \right)}\right)\circ \left(S_{\left(D\right)}\circ S_{\left(\Delta \right)}\right)$.

Soit $\left(\mathcal{C}\right)$ un cercle de centre $O$ et $A$ et $B$ deux points distincts de $\left(\mathcal{C}\right)$.

Soit $M$ un point de $\left(\mathcal{C}\right)$ distinct de $A$ et $B$.

On note $\left(\Delta \right)$ et $\left(\Delta \text{'}\right)$ les médiatrices respectives des segments $\left[AM\right]$ et $\left[BM\right]$.

3. Déterminer $S_{\left(\Delta \text{'}\right)}\circ S_{\left(\Delta \right)}$ et $S_{\left(BM\right)}\circ S_{\left(AM\right)}$.

Soit $ABCD$ un carré tel que : $\left(\overline{\overrightarrow{AB};\overrightarrow{AD}}\right)\equiv \frac{\mathrm{\pi }}{2} \left[2\mathrm{\pi }\right]$

Soit $r$ la rotation de centre $B$ et d'angle $\frac{\mathrm{\pi }}{4}$.

4. Montrer que $r$ est la composée des deux symétries orthogonale dont on déterminera les axes.

II- Propriétés des rotations

2-1/ Conservation de la distance

Proposition

Soit $A$ et $B$ sont deux points du plan $\mathcal{P}$.

Si $r\left(A\right)=A\text{'}$ et $r\left(B\right)=B\text{'}$, alors : $AB=A\text{'}B\text{'}$

On dit que la rotation conserve la distance.

II- Propriétés des rotations

2-2/ Conservation des mesures des angles orientés

Proposition

Soit $A$ et $B$ sont deux points du plan $\mathcal{P}$.

Si $r\left(A\right)=A\text{'}$ et $r\left(B\right)=B\text{'}$, alors : $\left(\overline{\overrightarrow{AB};\overrightarrow{A\text{'}B\text{'}}}\right)\equiv \theta \left[2\mathrm{\pi }\right]$

(On rappelle que $\theta$ désigne l’angle de la rotation $r$)

Remarque

La propriété précédente permet de déterminer l'angle d'une rotation à partir de deux points distincts et leurs images.

II- Propriétés des rotations

2-2/ Conservation des mesures des angles orientés

Proposition

Soit  $A$, $B$, $C$ et $D$ quatre points du plan $\mathcal{P}$ tels que $A\ne B$ et $C\ne D$.

Soit $A\text{'}$, $B\text{'}$, $C\text{'}$ et $D\text{'}$ leurs images respectives par la rotation $r$.

Alors : $\left(\overline{\overrightarrow{AB};\overrightarrow{CD}}\right)\equiv \left(\overline{\overrightarrow{A\text{'}B\text{'}};\overrightarrow{C\text{'}D\text{'}}}\right) \left[2\mathrm{\pi }\right]$

On dit que la rotation conserve les mesures des angles orientés.

II- Propriétés des rotations

2-3/ Conservation du coefficient de colinéarité de deux vecteurs

Proposition

Soit  $A$, $B$ et $C$ trois points alignés tels que $\overrightarrow{AC}=k\overrightarrow{AB}$ où $k\in \mathrm{ℝ}$.

Si $r\left(A\right)=A\text{'}$, $r\left(B\right)=B\text{'}$ et $r\left(C\right)=C\text{'}$, alors : $\overrightarrow{A\text{'}C\text{'}}=k\overrightarrow{A\text{'}B\text{'}}$

On dit que la rotation conserve l'alignement des points et le coefficient de colinéarité de deux vecteurs.

II- Propriétés des rotations

2-3/ Conservation du coefficient de colinéarité de deux vecteurs

Applications

Soit $ABC$ un triangle tel que la mesure principale de l'angle $\left(\widehat{\overrightarrow{AB};\overrightarrow{AC}}\right)$ est positif.

On construit en dehors du triangle $ABC$ des carrés $ACDE$, $BAFG$ et $CBHI$.

1. En utilisant une rotation convenable, montrer que les droites $\left(AI\right)$ et $\left(BD\right)$ sont perpendiculaires.

2. Montrer que les droites $\left(AH\right)$ et $\left(CG\right)$ sont perpendiculaires.

On considère la rotation $r$ de centre $A$ et d'angle $\frac{\mathrm{\pi }}{2}$.

Soit $J$ le milieu du segment $\left[EF\right]$.

On pose : $r\left(J\right)=J\text{'}$

3. a- Montrer que le point $J\text{'}$ appartient à la droite passant par $A$ et parallèle à la droite $\left(BC\right)$.

3. b- En déduire que $\left(AJ\right)$ est une hauteur du triangle $ABC$.

II- Propriétés des rotations

2-4/ Conservation du barycentre

Proposition

Soit $G$ le barycentre du système pondéré $\left\{\left(A;\alpha \right);\left(B;\beta \right)\right\}$ tel que $\alpha +\beta \ne 0$.

Si $r\left(A\right)=A\text{'}$, $r\left(B\right)=B\text{'}$ et $r\left(G\right)=G\text{'}$, alors $G\text{'}$ est le barycentre du système $\left\{\left(A\text{'};\alpha \right);\left(B\text{'};\beta \right)\right\}$.

On dit que la rotation conserve le barycentre.

Remarques

On peut étendre cette propriété au barycentre de trois ou quatre points pondérés.

La rotation conserve le milieu d'un segment et le centre de gravité d'un triangle.

II- Propriétés des rotations

2-4/ Conservation du barycentre

Applications

Soit $ABCD$ et $AEFG$ deux carrés tels que :

$\left(\overline{\overrightarrow{AB};\overrightarrow{AD}}\right)\equiv \frac{\mathrm{\pi }}{2} \left[2\mathrm{\pi }\right]$ et $\left(\overline{\overrightarrow{AE};\overrightarrow{AG}}\right)\equiv \frac{\mathrm{\pi }}{2} \left[2\mathrm{\pi }\right]$ et $\left(\overline{\overrightarrow{AD};\overrightarrow{AE}}\right)\equiv \frac{\mathrm{\pi }}{2} \left[2\mathrm{\pi }\right]$ et $AE=AB$.

Soit $r$ la rotation de centre $A$ et transformant le point $B$ en $E$.

1. a- Déterminer une mesure de l'angle de la rotation $r$.

1. b- Montrer que $r\left(C\right)=F$ et $r\left(D\right)=G$.

1. c- Déterminer la mesure principale de l'angle orienté $\left(\widehat{\overrightarrow{BC};\overrightarrow{EF}}\right)$.

Soit $G$ le barycentre des points pondérés $\left(A;1\right)$, $\left(B;-1\right)$ et $\left(C;-1\right)$.

On pose : $r\left(G\right)=G\text{'}$

2. Montrer que les points $G$, $F$ et $G\text{'}$ sont alignés.

III- Images de certaines figures par une rotation

3-1/ Image d'un cercle par une rotation

Proposition

L'image du cercle $\mathcal{C}\left(O;R\right)$, de centre $O$ et de rayon $R$, est le cercle $\mathcal{C}\text{'}\left(O\text{'};R\right)$ où $O\text{'}=r\left(O\right)$.

III- Images de certaines figures par une rotation

3-2/ Image d'une droite, d'une demi-droite et d'un segment

Proposition

Soit $A$ et $B$ deux points distincts du plan.

Si $r\left(A\right)=A\text{'}$ et $r\left(B\right)=B\text{'}$, alors :

$r\left(\left(AB\right)\right)=\left(A\text{'}B\text{'}\right)$ et $r\left(\left[AB\right]\right)=\left[A\text{'}B\text{'}\right]$ et $r\left(\left[AB\right)\right)=[A\text{'}B\text{'})$

III- Images de certaines figures par une rotation

3-2/ Image d'une droite, d'une demi-droite et d'un segment

Remarques

- La rotation conserve le parallélisme : les images de deux droites parallèles par une rotation sont deux droites parallèles.

- La rotation conserve l’orthogonalité: les images de deux droites perpendiculaires par une rotation sont deux droites perpendiculaires.

- L'image d'un triangle isocèle par une rotation est un triangle isocèle.

- L'image d'un triangle rectangle par une rotation est un triangle rectangle.

- L'image d'un triangle équilatéral par une rotation est un triangle équilatéral.

- L'image d'un rectangle par une rotation est un rectangle.

- L'image de l'intersection de deux figures par une rotation est l'intersection des images de ces deux figures par cette rotation : Si $\left(F_1\right)$ et $\left(F_2\right)$ sont deux figures géométriques, alors :

$r\left(\left(F_1\right)\cap \left(F_2\right)\right)=r\left(\left(F_1\right)\right)\cap r\left(\left(F_2\right)\right)$

III- Images de certaines figures par une rotation

3-2/ Image d'une droite, d'une demi-droite et d'un segment

Applications

Soit $ABCD$ un carré tel que : $\left(\overline{\overrightarrow{AB};\overrightarrow{AD}}\right)\equiv \frac{\mathrm{\pi }}{2} \left[2\mathrm{\pi }\right]$

Soit $I$ un point du segment $\left[BD\right]$, et $\left(\mathcal{C}\right)$ le cercle de centre $I$ et de rayon $IA$.

Le cercle $\left(\mathcal{C}\right)$ coupe la droite $\left(AB\right)$ en $J$ et la droite $\left(AD\right)$ en $K$.

1. Construire une figure convenable.

2. Montrer que $BJ=DK$ et $\left(CI\right)\perp \left(JK\right)$.

IV- Composition de deux rotations

Théorème

Soit $r_1\left({\Omega }_1;{\alpha }_1\right)$ et $r_2\left({\Omega }_2;{\alpha }_2\right)$ deux rotations du plan d’angles non nuls.

- Si ${\Omega }_1={\Omega }_2$, alors $r_1\circ r_2$ est la rotation de centre ${\Omega }_1$ et d’angle ${\alpha }_1+{\alpha }_2$.

De plus, on a dans ce cas : $r_1\circ r_2=r_2\circ r_1$

- Si ${\Omega }_1\ne {\Omega }_2$ et ${\alpha }_1+{\alpha }_2\ne 2k\mathrm{\pi } \left(\mathrm{k}\in \mathrm{\mathbb{Z}}\right)$, alors $r_1\circ r_2$ est une rotation d’angle .

- Si ${\Omega }_1\ne {\Omega }_2$ et ${\alpha }_1+{\alpha }_2=2k\mathrm{\pi } \left(\mathrm{k}\in \mathrm{\mathbb{Z}}\right)$, alors $r_1\circ r_2$ est une translation.

Remarque

Dans le cas où ${\Omega }_1\ne {\Omega }_2$ et ${\alpha }_1+{\alpha }_2=2k\mathrm{\pi } \left(\mathrm{k}\in \mathrm{\mathbb{Z}}\right)$, alors pour déterminer le vecteur de la translation, il suffit de déterminer l’image d’un point connu par la translation $r_1\circ r_2$.

Si par exemple $r_1\circ r_2\left(O\right)=O\text{'}$, alors le vecteur de la translation est $\overrightarrow{OO\text{'}}$ : $r_1\circ r_2=t_{\overrightarrow{OO\text{'}}}$

IV- Composition de deux rotations

Théorème

Soit $ABC$ un triangle équilatéral de centre de gravité $G$ tel que : $\left(\overline{\overrightarrow{AB};\overrightarrow{AC}}\right)\equiv \frac{\mathrm{\pi }}{3} \left[2\mathrm{\pi }\right]$

1. Déterminer la nature de chacune des applications suivantes :

$$\begin{gathered} \boxed{1} r\left(G;\frac{\mathrm{\pi }}{3}\right)\circ r\left(G;-\frac{\mathrm{\pi }}{3}\right) \\ \boxed{2} r\left(C;\frac{\mathrm{\pi }}{3}\right)\circ r\left(B;-\frac{\mathrm{\pi }}{3}\right) \\ \boxed{3} r\left(C;\frac{\mathrm{\pi }}{3}\right)\circ r\left(B;\frac{\mathrm{\pi }}{3}\right) \\ \boxed{4} r\left(A;\frac{\mathrm{\pi }}{3}\right)\circ r\left(I;\frac{2\mathrm{\pi }}{3}\right) \end{gathered}$$