Séance 7-2-1 : Étude analytique du produit scalaire - Partie 2 (Cours)

Sommaire

V- Équation cartésienne d'un cercle

5-1/ Le cercle

5-2/ Équation cartésienne d'un cercle

5-3/ Équation d'un cercle défini par l'un de ses diamètres

5-4/ Équation d'un cercle défini par trois points non alignés

VI- Représentation paramétrique d'un cercle

VII- Ensemble des points $M(x;y)$ du plan tels que $x^2+y^2+ax+by+c=0$

IIX- Intérieur et extérieur d'un cercle

IX- Positions relatives d'une droite et d'un cercle

X- Équation cartésienne d'une droite tangente à un cercle en un point donné de ce cercle

V- Équation cartésienne d'un cercle

5-1/ Le cercle

Définition

Soit $\Omega$ un point du plan $\mathcal{P}$ et $R$ un réel positif.

Le cercle $\left(\mathcal{C}\right)$ de centre $\Omega$ et de rayon $R$ est l'ensemble des points $M$ du plan tels que $\Omega M=R$.

On le note : $\mathcal{C}\left(\Omega ;R\right)$

On a alors : $\mathcal{C}\left(\Omega ;R\right)\iff \Omega M=R$

V- Équation cartésienne d'un cercle

5-2/ Équation cartésienne d'un cercle

Proposition

Une équation cartésienne du cercle $\left(\mathcal{C}\right)$ de centre $\Omega \left(a;b\right)$ et de rayon $R \left(R\ge 0\right)$ est :

${\left(x-a\right)}^2+{\left(y-b\right)}^2=R^2$

que l’on peut écrire $x^2+y^2-2ax-2by+c=0$ où $c=a^2+b^2-R^2$.

V- Équation cartésienne d'un cercle

5-2/ Équation cartésienne d'un cercle

Applications

1. Écrire une équation cartésienne du cercle $\left(\mathcal{C}\right)$ de centre $\Omega$ et de rayon $R$ dans chacun des cas suivants :

$$\begin{gathered} \boxed{1} \Omega \left(2;4\right) et R=3 \\ \boxed{2} \Omega \left(-\frac{1}{2};\frac{3}{2}\right) et R=2\sqrt{2} \\ \boxed{3} \Omega \left(-1;-3\right) et R=\frac{\sqrt{3}}{2} \end{gathered}$$

2. Écrire une équation du cercle cercle $\left(\mathcal{C}\right)$ de centre $\Omega$ et passant par le point $A$ dans chacun des cas suivants :

$$\begin{gathered} \boxed{1} \Omega \left(2;0\right) et A\left(2;4\right) \\ \boxed{2} \Omega \left(1;2\right) et A\left(4;-2\right) \\ \boxed{3} \Omega \left(-2;3\right) et A\left(2;-1\right) \end{gathered}$$

V- Équation cartésienne d'un cercle

5-3/ Équation d'un cercle défini par l'un de ses diamètres

Proposition

Soit $A$ et $B$ deux points distincts dans le plan $\mathcal{P}$.

L’ensemble des points $M$ du plan tels que $\overrightarrow{AM}.\overrightarrow{BM}=0$ est le cercle $\left(\mathcal{C}\right)$ de diamètre $\left[AB\right]$.

Le centre du cercle $\left(\mathcal{C}\right)$ est le point $\Omega$ milieu du segment $\left[AB\right]$, et son rayon est $R=\frac{AB}{2}$.

Si $A\left(x_A;y_A\right)$, $B\left(x_B;y_B\right)$ et $M\left(x,y\right)$, alors une équation cartésienne du cercle $\left(\mathcal{C}\right)$ est :

$\left(x-x_A\right)\left(x-x_B\right)+\left(y-y_A\right)\left(y-y_B\right)=0$

Autrement dit :

$x^2+y^2-\left(x_A+x_B\right)x-\left(y_A+y_B\right)y+\left(x_A.x_B+y_A.y_B\right)=0$

V- Équation cartésienne d'un cercle

5-3/ Équation d'un cercle défini par l'un de ses diamètres

Applications

1. Déterminer une équation cartésienne du cercle $\left(\mathcal{C}\right)$ de diamètre $\left[AB\right]$ dans chacun des cas suivants :

$$\begin{gathered} \boxed{1} A\left(1;3\right) et B\left(2;1\right) \\ \boxed{2} A\left(-2;4\right) et B\left(2;3\right) \\ \boxed{3} A\left(-3;1\right) et B\left(2;5\right) \end{gathered}$$

V- Équation cartésienne d'un cercle

5-4/ Équation d'un cercle défini par trois points non alignés

Proposition

Par trois points non alignés $A$, $B$ et $C$ passe un seul cercle de centre $\left(\mathcal{C}\right)$ le point d'intersection des médiatrices du triangle $ABC$, et de rayon $R=\Omega A$.

Ce cercle est appelé le cercle circonscrit au triangle $ABC$.

V- Équation cartésienne d'un cercle

5-4/ Équation d'un cercle défini par trois points non alignés

Applications

1. Déterminer une équation du cercle $\left(\mathcal{C}\right)$ circonscrit au triangle $ABC$ dans les deux cas suivants :

$$\begin{gathered} \boxed{1} A\left(2;1\right) et B\left(4;-1\right) et C\left(0;3\right) \\ \boxed{2} A\left(3;-1\right) et B\left(5;3\right) et C\left(1:1\right) \end{gathered}$$

VI- Représentation paramétrique d'un cercle

Proposition

Le cercle $\left(\mathcal{C}\right)$ de centre $\Omega \left(a;b\right)$ et de rayon $R$ est l'ensemble des points $M\left(x,y\right)$ du plan qui vérifient le système :

$\left\{\begin{array}{l}x=a+R\cos \theta \\ y=b+R\sin \theta \end{array}\right. \left(\theta \in \mathrm{ℝ}\right)$

Ce système est appelé une représentation paramétrique du cercle $\left(\mathcal{C}\right)$.

VI- Représentation paramétrique d'un cercle

Applications

1. Donner une représentation paramétrique du cercle $\left(\mathcal{C}\right)$ dans les cas suivants :

$$\begin{gathered} \boxed{1} x^2+y^2-2x-6y-6=0 \\ \boxed{2} x^2+y^2+4x-16=0 \\ \boxed{3} x^2+y^2+6x-8y+23=0 \end{gathered}$$

2. Déterminer l'ensemble $\left(E\right)$ des points $M\left(x,y\right)$ du plan tels que :

$\left\{\begin{array}{l}x=\sqrt{2}\cos \theta \\ y=4+\sqrt{2}\sin \theta \end{array}\right. \left(\theta \in \mathrm{ℝ}\right)$

3. Déterminer une équation cartésienne du cercle $\left(\mathcal{C}\right)$ de représentation paramétrique :

$\left\{\begin{array}{l}x=1+3\cos t\\ y=-1+3\sin t\end{array}\right. \left(t\in \mathrm{ℝ}\right)$

VII- Ensemble des points $M(x;y)$ du plan tels que $x^2+y^2+ax+by+c=0$

Proposition

Soit $\left(\Gamma \right)$ l'ensemble des points $M\left(x,y\right)$ du plan $\mathcal{P}$ vérifiant l'équation $x^2+y^2+ax+by+c=0$ où $\left(a;b;c\right)\in {\mathrm{ℝ}}^3$

On pose : $k=a^2+b^2-4c$

- Si $k<0$, alors l'ensemble $\left(\Gamma \right)$ est vide : $\left(\Gamma \right)=\varnothing$

- Si $k=0$, alors l'ensemble $\left(\Gamma \right)$ est un singleton : $\left(\Gamma \right)=\left\{\Omega \left(-\frac{a}{2};-\frac{b}{2}\right)\right\}$

- Si $k>0$, alors l'ensemble $\left(\Gamma \right)$ est le cercle de centre $\Omega \left(-\frac{a}{2};-\frac{b}{2}\right)$ et de rayon $R=\frac{\sqrt{k}}{2}$.

VII- Ensemble des points $M(x;y)$ du plan tels que $x^2+y^2+ax+by+c=0$

Applications

1. Déterminer l'ensemble $\left(E\right)$ des points $M\left(x,y\right)$ vérifiant l'équation cartésienne correspondante à chacun des cas suivants :

IIX- Intérieur et extérieur d'un cercle

Définition

Soit $\left(\mathcal{C}\right)$ le cercle de centre $\Omega$ et de rayon $R>0$, et $M$ un point du plan $\mathcal{P}$.

- Le point $M$ est sur le cercle $\left(\mathcal{C}\right)$ si et seulement si : $\Omega M=R$

- Le point $M$ est à l'intérieur du cercle $\left(\mathcal{C}\right)$ si et seulement si : $\Omega M<R$

- Le point $M$ est à l'extérieur du cercle $\left(\mathcal{C}\right)$ si et seulement si : $\Omega M>R$

IIX- Intérieur et extérieur d'un cercle

Proposition

Soit $\left(\mathcal{C}\right)$ le cercle d'équation cartésienne $x^2+y^2+ax+by+c=0$ où $\left(a;b;c\right)\in {\mathrm{ℝ}}^3$.

Pour tout point $M\left(x_0;y_0\right)$ du plan :

- $M$ est un point du cercle $\left(\mathcal{C}\right)$ si et seulement si : ${x_0}^2+{y_0}^2+a{x}_0+b{y}_0+c=0$

- $M$ est à l’intérieur du cercle $\left(\mathcal{C}\right)$ si et seulement si : ${x_0}^2+{y_0}^2+a{x}_0+b{y}_0+c<0$

- $M$ est à l'extérieur du cercle $\left(\mathcal{C}\right)$ si et seulement si : ${x_0}^2+{y_0}^2+a{x}_0+b{y}_0+c>0$

Ainsi, le cercle $\left(\mathcal{C}\right)$ détermine trois parties disjointes dans le plan $\mathcal{P}$.

IIX- Intérieur et extérieur d'un cercle

Applications

1. Déterminer la position du point $A$ par rapport au cercle $\left(\mathcal{C}\right)$ dans chacun des cas suivants :

a) $\left(\mathcal{C}\right)$ le cercle de centre $\Omega \left(2;3\right)$ et de rayon $R=1$ et le point $A\left(-1;2\right)$.

b) $\left(\mathcal{C}\right) : x^2+y^2-2x+4y=0$ et le point $A\left(0;1\right)$.

c)  $\left(\mathcal{C}\right) : \left\{\begin{array}{l}x=1+2\cos \theta \\ y=1+2\sin \theta \end{array}\right. \left(\theta \in \mathrm{ℝ}\right)$ et le point $A\left(2;1\right)$.

2. Résoudre graphiquement les inéquations suivantes :

$$\begin{gathered} \boxed{1} x^2+y^2+2x-6y+9\ge 0 \\ \boxed{2} x^2+y^2+2y-3<0 \\ \boxed{3} x^2+y^2<4 \end{gathered}$$

3. Résoudre graphiquement les systèmes suivants :

$$\begin{gathered} \boxed{1} \left\{\begin{array}{l}{x}^2+y^2-2x+2y-7<0\\ x-y>0\end{array}\right. \\ \boxed{2} \left\{\begin{array}{l}{x}^2+y^2-x-2y-\frac{11}{4}\ge 0\\ x+2y-3<0\end{array}\right. \\ \boxed{3} \left\{\begin{array}{c}{x}^2+y^2+10x-4y+25<0\\ x+2y-3>0 \\ 3x+y+11\le 0 \end{array}\right. \end{gathered}$$

IX- Positions relatives d'une droite et d'un cercle

Proposition

Soit $\left(\mathcal{C}\right)$ le cercle de centre $\Omega$ et de rayon $R$, et $\left(\mathcal{D}\right)$ une droite dans le plan $\mathcal{P}$ rapporté à un repère orthonormé.

- Si $d\left(\Omega ;\left(\mathcal{D}\right)\right)>R$, alors l'intersection de $\left(\mathcal{D}\right)$ et $\left(\mathcal{C}\right)$ est vide : (2)) n (S?) = 0.

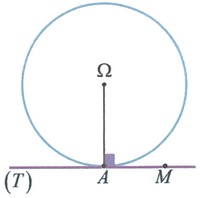
- Si $d\left(\Omega ;\left(\mathcal{D}\right)\right)=R$, alors l'intersection de $\left(\mathcal{D}\right)$ et $\left(\mathcal{C}\right)$ est le singleton $\left\{H\right\}$ où $H$ est le point de contact (ou de tangence) de la droite $\left(\mathcal{D}\right)$ et du cercle $\left(\mathcal{C}\right)$.

- Si $d\left(\Omega ;\left(\mathcal{D}\right)\right)>R$, alors l'intersection de $\left(\mathcal{D}\right)$ et $\left(\mathcal{C}\right)$ est un bipoint $\left\{A;B\right\}$.

IX- Positions relatives d'une droite et d'un cercle

Applications

1. Étudier l’intersection de la droite $\left(\mathcal{D}\right)$ et du cercle $\left(\mathcal{C}\right)$ dans chacun des cas suivants :

$$\begin{gathered} \boxed{1} \left(\mathcal{C}\right) : x^2+y^2-4x+2y=0 et \left(\mathcal{D}\right) : 2x-y=0 \\ \boxed{2} \left(\mathcal{C}\right) : {\left(x+2\right)}^2+{\left(y+2\right)}^2=2 et \left(\mathcal{D}\right) : x-y-2=0 \\ \boxed{3} \left(\mathcal{C}\right) : x^2+y^2-2x+4y-11=0 et \left(\mathcal{D}\right) : x+y-3=0 \end{gathered}$$

X- Équation cartésienne d'une droite tangente à un cercle en un point donné de ce cercle

Proposition

Soit $\left(\mathcal{C}\right)$ le cercle de centre $\Omega$ et de rayon $R$, et $A\left(x_0;y_0\right)$ un point du cercle $\left(\mathcal{C}\right)$, et $\left(T\right)$ la tangente au cercle $\left(\mathcal{C}\right)$ au point $A$.

La droite $\left(T\right)$ est l'ensemble des points $M\left(x;y\right)$ du plan tels que : $\overrightarrow{A\Omega }.\overrightarrow{AM}=0$

Si le cercle $\left(\mathcal{C}\right)$ admet une équation cartésienne de la forme $x^2+y^2+ax+by+c=0$, alors une équation de la tangente $\left(T\right)$ est donnée par :

$\left(T\right) : x{x}_0+y{y}_0+\frac{1}{2}a\left(x+x_0\right)+\frac{1}{2}b\left(y+y_0\right)+c=0$