Séance 7-1-1 : Étude analytique du produit scalaire - Partie 1 (Cours)

Sommaire

I- Étude analytique du produit scalaire

1-1/ Expression analytique du produit scalaire

1-2/ Expression analytique de la norme d'un vecteur et de la distance de deux points

1-3/ Inégalité de Cauchy-Schwarz

1-4/ Inégalité triangulaire

II- Produit scalaire et angles

2-1/ Repérage polaire d'un vecteur

2-2/ Expression de $\cos \left(\widehat{\overrightarrow{u};\overrightarrow{v}}\right)$ et $\sin \left(\widehat{\overrightarrow{u};\overrightarrow{v}}\right)$

2-3/ Aire d'un triangle

III- Étude analytique de la droite dans le plan

3-1/ Vecteur normal à une droite

3-2/ Équation d'une droite définie par un point et un vecteur normal à cette droite

3-3/ Condition de perpendicularité de deux droites

3-4/ Distance d'un point à une droite

I- Étude analytique du produit scalaire

1-1/ Expression analytique du produit scalaire

Proposition

Soit $\overrightarrow{u}=x\overrightarrow{i}+y\overrightarrow{j}$ et $\overrightarrow{v}=x\text{'}\overrightarrow{i}+y\text{'}\overrightarrow{j}$ deux vecteurs du plan.

Alors : $\overrightarrow{u}.\overrightarrow{v}=xx\text{'}+yy\text{'} ; \overrightarrow{i}.\overrightarrow{u}=x ; \overrightarrow{j}.\overrightarrow{v}=y$

I- Étude analytique du produit scalaire

1-1/ Expression analytique du produit scalaire

Applications

Soit les vecteurs $\overrightarrow{u}=\frac{3}{2}\overrightarrow{i}+5\overrightarrow{j}$ et $\overrightarrow{v}=-4\overrightarrow{i}+7\overrightarrow{j}$.

1. Calculer le produit scalaire $\overrightarrow{u}.\overrightarrow{v}$.

Soit les vecteurs $\overrightarrow{u}=\left(\sqrt{3}-1\right)\overrightarrow{i}+2\overrightarrow{j}$ et $\overrightarrow{v}=\left(\sqrt{3}+1\right)\overrightarrow{i}+\frac{3}{2}\overrightarrow{j}$.

2. A-t-on $\overrightarrow{u}\perp \overrightarrow{v}$ ? Justifier la réponse.

Soit les vecteurs $\overrightarrow{u}=\left(2m-1\right)\overrightarrow{i}+4m\overrightarrow{j}$ et $\overrightarrow{v}=3\overrightarrow{i}-2\overrightarrow{j}$ où $m\in \mathrm{ℝ}$.

3. Déterminer $m$ sachant que $\overrightarrow{u}\perp \overrightarrow{v}$.

I- Étude analytique du produit scalaire

1-2/ Expression analytique de la norme d'un vecteur et de la distance de deux points

Proposition

Si $\overrightarrow{u}=x\overrightarrow{i}+y\overrightarrow{j}$ est un vecteur du plan, alors sa norme est : $||\overrightarrow{u}||=\sqrt{x^2+y^2}$

Si $A\left(x_A;y_A\right)$ et $B\left(x_B;y_B\right)$ sont deux points du pian, alors : $AB=\sqrt{{\left(x_B-x_A\right)}^2+{\left(y_B-y_A\right)}^2}$

I- Étude analytique du produit scalaire

1-2/ Expression analytique de la norme d'un vecteur et de la distance de deux points

Applications

On considère les vecteurs $\overrightarrow{u}=2\overrightarrow{i}+3\overrightarrow{j}$, $\overrightarrow{v}\left(\sqrt{5}-2;\sqrt{5}+2\right)$ et $\overrightarrow{w}=\left(2m-1\right)\overrightarrow{i}+3\overrightarrow{j}$ où $m\in \mathrm{ℝ}$.

1. Calculer $||\overrightarrow{u}||$, $||\overrightarrow{v}||$ et $||\overrightarrow{w}||$.

2. Déterminer les valeurs de ni pour lesquelles $||\overrightarrow{w}||=\sqrt{10}$.

On considère dans le plan, les points $A\left(0;3\right)$, $B\left(-1;5\right)$ et $C\left(2m+1;m-1\right)$ où $m\in \mathrm{ℝ}$.

3. Calculer les distances $AB$, $AC$ et $BC$.

4. Est-ce-que le triangle $ABC$ peut être isocèle ? Justifier la réponse.

I- Étude analytique du produit scalaire

1-3/ Inégalité de Cauchy-Schwarz

Proposition

Soit $\overrightarrow{u}$ et $\overrightarrow{v}$ deux vecteurs du plan.

On a alors :

- L'inégalité de Cauchy-Schwarz : $\left|\overrightarrow{u}.\overrightarrow{v}\right|\le ||\overrightarrow{u}||.||\overrightarrow{v}||$

- L'égalité $\left|\overrightarrow{u}.\overrightarrow{v}\right|=||\overrightarrow{u}||.||\overrightarrow{v}||$ aura lieu si, et seulement si, les vecteurs $\overrightarrow{u}$ et $\overrightarrow{v}$ sont colinéaires.

I- Étude analytique du produit scalaire

1-4/ Inégalité triangulaire

Proposition

Soit $\overrightarrow{u}$ et $\overrightarrow{v}$ deux vecteurs du plan.

On a alors :

- L'inégalité triangulaire : $\left|\overrightarrow{u}+\overrightarrow{v}\right|\le ||\overrightarrow{u}||+||\overrightarrow{v}||$

- L'égalité $\left|\overrightarrow{u}+\overrightarrow{v}\right|=||\overrightarrow{u}||+||\overrightarrow{v}||$ aura lieu si, et seulement si, les vecteurs $\overrightarrow{u}$ et $\overrightarrow{v}$ sont colinéaires et ont le même sens.

I- Étude analytique du produit scalaire

1-4/ Inégalité triangulaire

Applications

1. En utilisant l'inégalité de Cauchy-Schwarz, Montrer que :

$\left(\forall \left(x;y\right)\in {\mathrm{ℝ}}^2\right) x+y\le \left(1+x^2\right)\left(1+y^2\right)$

Soit $\left(a;b;c;d\right)\in {\mathrm{ℝ}}^4$ tel que $a\ne 0$ et $b\ne 0$.

2. En utilisant l'inégalité de Cauchy-Schwarz, montrer que :

${\left(a-c\right)}^2+{\left(b-d\right)}^2\ge \frac{{\left(ad-bc\right)}^2}{a^2+b^2}$

3. Montrer, en utilisant l'inégalité de Cauchy-Schwarz, que pour tous réels $a_1,a_2,...,a_n,b_1,b_2,...,b_n$ :

$\sqrt{{\left(\sum _{i=1}^n{a}_i\right)}^2+{\left(\sum _{i=1}^n{b}_i\right)}^2}\le \sum _{i=1}^n\sqrt{{a_i}^2+{b_i}^2}$

II- Produit scalaire et angles

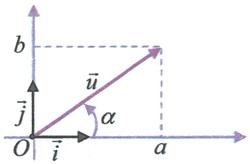
2-1/ Repérage polaire d'un vecteur

Proposition

Soit $\overrightarrow{u}$ un vecteur non nul du plan.

Si $\alpha$ désigne une mesure de l’angle $\left(\widehat{\overrightarrow{i};\overrightarrow{u}}\right)$, alors : $\overrightarrow{u}=||\overrightarrow{u}||.\left[\left(\cos \alpha \right)\overrightarrow{i}+\left(\sin \alpha \right)\overrightarrow{j}\right]$

Donc $a=||\overrightarrow{u}||.\cos \alpha$ et $b=||\overrightarrow{u}||.\sin \alpha$

II- Produit scalaire et angles

2-2/ Expression de $\cos \left(\widehat{\overrightarrow{u};\overrightarrow{v}}\right)$ et $\sin \left(\widehat{\overrightarrow{u};\overrightarrow{v}}\right)$

Proposition

Soit $\overrightarrow{u}=x\overrightarrow{i}+y\overrightarrow{j}$ et $\overrightarrow{v}=x\text{'}\overrightarrow{i}+y\text{'}\overrightarrow{j}$ deux vecteurs non nuls et $\theta$ une mesure de l’angle $\left(\widehat{\overrightarrow{u};\overrightarrow{v}}\right)$.

On a alors les formules suivantes :

$\cos \theta =\frac{\overrightarrow{u}.\overrightarrow{v}}{||\overrightarrow{u}||.||\overrightarrow{v}||}=\frac{xx\text{'}+yy\text{'}}{\sqrt{x^2+y^2}.\sqrt{x{\text{'}}^2+y{\text{'}}^2}}$ et $\cos \theta =\frac{det\left(\overrightarrow{u};\overrightarrow{v}\right)}{||\overrightarrow{u}||.||\overrightarrow{v}||}=\frac{xy\text{'}-yx\text{'}}{\sqrt{x^2+y^2}.\sqrt{x{\text{'}}^2+y{\text{'}}^2}}$

II- Produit scalaire et angles

2-2/ Expression de $\cos \left(\widehat{\overrightarrow{u};\overrightarrow{v}}\right)$ et $\sin \left(\widehat{\overrightarrow{u};\overrightarrow{v}}\right)$

Applications

1. Calculer $\cos \left(\widehat{\overrightarrow{u};\overrightarrow{v}}\right)$ et $\sin \left(\widehat{\overrightarrow{u};\overrightarrow{v}}\right)$ dans les deux cas suivants :

$$\begin{gathered} \boxed{1} \overrightarrow{u}=-\overrightarrow{i}+2\overrightarrow{j} et \overrightarrow{v}=3\overrightarrow{i}+4\overrightarrow{j} \\ \boxed{2} \overrightarrow{u}=\overrightarrow{i}-\overrightarrow{j} et \overrightarrow{v}=\left(\sqrt{3}-1\right)\overrightarrow{i}+\left(\sqrt{3}+1\right)\overrightarrow{j} \end{gathered}$$

On considère les points : $A\left(1;3\right)$, $B\left(3;1\right)$ et $C\left(-3;-1\right)$.

2. Calculer $\cos \left(\widehat{\overrightarrow{BA};\overrightarrow{BC}}\right)$ et $\sin \left(\widehat{\overrightarrow{BA};\overrightarrow{BC}}\right)$.

II- Produit scalaire et angles

2-3/ Aire d'un triangle

Proposition

L'aire du triangle ABC est : $S=\frac{1}{2}\left|det\left(\overrightarrow{AB};\overrightarrow{AC}\right)\right|$

Remarque

On a aussi : $S=\frac{1}{2}\left|det\left(\overrightarrow{BA};\overrightarrow{BC}\right)\right|=\frac{1}{2}\left|det\left(\overrightarrow{CA};\overrightarrow{CB}\right)\right|$

III- Étude analytique de la droite dans le plan

3-1/ Vecteur normal à une droite

Définition

Soit $\left(\mathcal{D}\right)$ une droite du plan.

Tout vecteur non nul et orthogonal à un vecteur directeur de la droite $\left(\mathcal{D}\right)$ est appelé vecteur normal à la droite $\left(\mathcal{D}\right)$.

III- Étude analytique de la droite dans le plan

3-1/ Vecteur normal à une droite

Proposition

Soit $\left(\mathcal{D}\right)$ une droite dans le plan $\mathcal{P}$ rapporté à un repère orthonormé $\left(O;\overrightarrow{i};\overrightarrow{j}\right)$.

- Si $\overrightarrow{n}$ et $\overrightarrow{n\text{'}}$ sont deux vecteurs normaux sur $\left(\mathcal{D}\right)$, alors ils sont colinéaires.

- Si $\overrightarrow{u}\left(\alpha ;\beta \right)$ est un vecteur directeur de $\left(\mathcal{D}\right)$, alors le vecteur $\overrightarrow{n}\left(-\beta ;\alpha \right)$ est normal à $\left(\mathcal{D}\right)$.

- Si une équation cartésienne de $\left(\mathcal{D}\right)$ est $ax+by+c=0$ avec $(a;b)\ne (0;0)$, alors le vecteur  est normal à la droite $\left(\mathcal{D}\right)$.

III- Étude analytique de la droite dans le plan

3-1/ Vecteur normal à une droite

Applications

On considère les droites $\left(\mathcal{D}\right): 5x+2y-3=0$ et $\left(\mathcal{D}\text{'}\right): y=2x-3$.

1. Les droites $\left(\mathcal{D}\right)$ et $\left(\mathcal{D}\text{'}\right)$ sont-elles orthogonales ? Justifier la réponse.

2. Déterminer un vecteur normal à la droite $\left(\mathcal{D}\right)$ dans chacun des cas suivants :

$$\begin{gathered} \boxed{1} \left(\mathcal{D}\right) : x+y+3=0 \\ \boxed{2} \left(\mathcal{D}\right) : y=x \\ \boxed{3} \left(\mathcal{D}\right) : x=3 \\ \boxed{4} \left(\mathcal{D}\right) : 2x-1=0 \end{gathered}$$

III- Étude analytique de la droite dans le plan

3-2/ Équation d'une droite définie par un point et un vecteur normal à cette droite

Proposition

Soit $\overrightarrow{n}$ un vecteur non nul et $A$ un point du plan $\mathcal{P}$.

L'ensemble des points $M$ du plan $\mathcal{P}$ tels que $\overrightarrow{AM}.\overrightarrow{n}=0$ est la droite $\left(\mathcal{D}\right)$ passant par $A$ et de vecteur normal $\overrightarrow{n}$.

Si $A\left(x_A;y_A\right)$ et $\overrightarrow{n}\left(a;b\right)$, alors une équation cartésienne de la droite $\left(\mathcal{D}\right)$ est :

$\left(\mathcal{D}\right): a\left(x-x_A\right)+b\left(y-y_A\right)=0$

III- Étude analytique de la droite dans le plan

3-2/ Équation d'une droite définie par un point et un vecteur normal à cette droite

Applications

1. Écrire une équation cartésienne de la droite $\left(\mathcal{D}\right)$ passant par le point $A$ et de vecteur normal $\overrightarrow{n}$ dans chacun des cas suivants :

$$\begin{gathered} \boxed{1} A\left(2;1\right) et \overrightarrow{n}\left(3;-2\right) \\ \boxed{2} A\left(-\frac{1}{2};3\right) et \overrightarrow{n}=2\overrightarrow{j} \\ \boxed{3} A\left(1;\sqrt{3}\right) et \overrightarrow{n}=\frac{1}{2}\overrightarrow{i}-\frac{\sqrt{3}}{2}\overrightarrow{j} \end{gathered}$$

Dans le plan rapporté à un repère orthonormé $\left(O;\overrightarrow{i};\overrightarrow{j}\right)$, on considère le point $A(0;2)$ et la droite $\left(D\right)$ d'équation cartésienne $2x+\sqrt{7}y-6=0$.

2. Déterminer une équation cartésienne de la droite $\left(\Delta \right)$ passant par le point $A$ et orthogonale à $\left(D\right)$.

III- Étude analytique de la droite dans le plan

3-3/ Condition de perpendicularité de deux droites

Proposition

Soit $\left(\mathcal{D}\right)$ et $\left(\mathcal{D}\text{'}\right)$ deux droites du plan $\mathcal{P}$.

- Si $\overrightarrow{n}$ et $\overrightarrow{n\text{'}}$ sont deux vecteurs normaux respectivement aux droites $\left(\mathcal{D}\right)$ et $\left(\mathcal{D}\text{'}\right)$, alors :

$\left(\mathcal{D}\right)\perp \left(\mathcal{D}\text{'}\right)\iff \overrightarrow{n}\perp \overrightarrow{n\text{'}}\iff \overrightarrow{n}.\overrightarrow{n\text{'}}=0$

- Si les droites $\left(\mathcal{D}\right)$ et $\left(\mathcal{D}\text{'}\right)$ sont définies respectivement par les équations cartésiennes $ax+by+c=0$ et $a\text{'}x+b\text{'}y+c\text{'}=0$, alors :

$\left(\mathcal{D}\right)\perp \left(\mathcal{D}\text{'}\right)\iff aa\text{'}+bb\text{'}=0$

III- Étude analytique de la droite dans le plan

3-3/ Condition de perpendicularité de deux droites

Applications

On considère les droites $\left(D\right): 5x+2y-3=0$ et $\left(D\text{'}\right): y=2x-3$.

1. Les droites $\left(D\right)$ et $\left(D\text{'}\right)$ sont-elles perpendiculaires ? Justifier la réponse.

On considère les droites $\left({\Delta }_1\right): \left(2m-3\right)x-5y+11=0$ et $\left({\Delta }_2\right): 2x+3y+5=0$ où $m\in \mathrm{ℝ}$.

2. Déterminer la valeur de $m$ pour que les droites $\left({\Delta }_1\right)$ et $\left({\Delta }_2\right)$ soient perpendiculaires.

On considère les points $A(1;2)$, $B(-3;-6)$, $C(0;1)$ et $D(2;0)$.

3. Montrer que $\left(AB\right)\perp \left(CD\right)$.

III- Étude analytique de la droite dans le plan

3-4/ Distance d'un point à une droite

Proposition

Soit $\left(\mathcal{D}\right)$ une droite d'équation $ax+by+c=0$ avec $\left(a;b\right)\ne \left(0;0\right)$ et $A\left(x_A;y_A\right)$ un point du plan.

La distance du point $A$ à la droite $\left(\mathcal{D}\right)$ est donnée par :

$d\left(A;\left(\mathcal{D}\right)\right)=\frac{\left|a{x}_A+b{y}_A+c\right|}{\sqrt{a^2+b^2}}$

III- Étude analytique de la droite dans le plan

3-4/ Distance d'un point à une droite

Applications

1. Calculer la distance du point $A$ à la droite $\left(\mathcal{D}\right)$ dans chacun des cas suivants :

$$\begin{gathered} \boxed{1} A\left(2;3\right) et \left(\mathcal{D}\right): 2x-5y+4=0 \\ \boxed{2} A\left(-2;3\right) et \left(\mathcal{D}\right): x-3y+5=0 \\ \boxed{3} A\left(-4;3\right) et \left(\mathcal{D}\right): 3x-5=0 \\ \boxed{4} A\left(0;1\right) et \left(\mathcal{D}\right): y=-2x+3 \end{gathered}$$

Dans le plan rapporté à un repère orthonormé $\left(O;\overrightarrow{i};\overrightarrow{j}\right)$, on considère les points $A\left(1;-1\right)$, $B\left(-1;2\right)$ et $C\left(-3;-2\right)$.

2. Déterminer une équation cartésienne de la droite $\left(AB\right)$.

3. Calculer $d\left(C;\left(AB\right)\right)$, puis en déduire l’aire du triangle $ABC$.

4. Déterminer le couple de coordonnées du point $H$ projeté orthogonal du point $C$ sur la droite $\left(AB\right)$.