Séance 4-2-1 : Généralités sur les fonctions - Partie 2 (Cours)

Sommaire

VII- Représentation graphique de quelques fonctions usuelles

7-1/ La fonction trinôme du second degré - parabole

7-2/ La fonction homographique - hyperbole

7-3/ La fonction $x\mapsto a{x}^3 \left(a\in \mathrm{ℝ}\right)$

7-4/ La fonction $x\mapsto \sqrt{x+a} \left(a\in \mathrm{ℝ}\right)$

7-5/ La fonction partie entière

IIX- Composée de deux fonctions numériques

IX- Fonction périodique

VII- Représentation graphique de quelques fonctions usuelles

7-1/ La fonction trinôme du second degré - parabole

Soit $f$ la fonction définie sur $\mathrm{ℝ}$ par $f\left(x\right)=a{x}^2+bx+c$ où $a$, $b$ et $c$ sont des réels avec $a\ne 0$.

• Tableaux de variations :

• Courbes représentatives :

${\mathcal{C}}_f$ est une parabole de sommet $\Omega \left(-\frac{b}{2a};f\left(-\frac{b}{2a}\right)\right)$ et d'axe de symétrie d'équation $x=-\frac{b}{2a}$.

VII- Représentation graphique de quelques fonctions usuelles

7-1/ La fonction trinôme du second degré - parabole

Applications

1. Dresser le tableau de variations de chacune des fonctions suivantes puis tracer sa courbe représentative :

.$f\left(x\right)=-2x^2+x+1 ; g\left(x\right)=x^2+2x+2 ; h\left(x\right)=-x^2+\left|x\right|$

VII- Représentation graphique de quelques fonctions usuelles

7-2/ La fonction homographique - hyperbole

Soit $f$ la fonction numérique définie sur $\mathrm{ℝ}-\left\{-\frac{d}{c}\right\}$ par $f\left(x\right)=\frac{ax+b}{cx+d}$ où $a$, $b$, $c$ et $d$ sont des réels avec $c\ne 0$, et $ad-bc\ne 0$.

On pose : $\Delta =\left|\begin{array}{cc}a& b\\ c& d\end{array}\right|=ad-bc$

• Tableaux de variations :

• Courbes représentatives :

${\mathcal{C}}_f$ est une hyperbole de centre $\Omega \left(-\frac{d}{c};\frac{a}{c}\right)$ et d'asymptotes les droites d'équations $x=-\frac{d}{c}$ et $y=\frac{a}{c}$.

VII- Représentation graphique de quelques fonctions usuelles

7-2/ La fonction homographique - hyperbole

Applications

1. Dresser le tableau de variations de chacune des fonctions suivantes puis tracer sa courbe représentative :

.$f\left(x\right)=\frac{2x+1}{x-1} ; g\left(x\right)=\frac{3x+1}{x+1} ; h\left(x\right)=-1+\frac{1}{x} ; k\left(x\right)=\frac{\left|x\right|}{\left|x\right|+2}$

VII- Représentation graphique de quelques fonctions usuelles

7-3/ La fonction $x\mapsto a{x}^3 \left(a\in \mathrm{ℝ}\right)$

Soit $f$ la fonction définie sur $\mathrm{ℝ}$ par $f\left(x\right)=a{x}^3$ où $a$ est un réel non nul.

• Tableaux de variations :

• Courbes représentatives :

La fonction $f : x\mapsto a{x}^3$ est impaire et sa courbe ${\mathcal{C}}_f$ est symétrique par rapport à l’origine du repère.

La courbe ${\mathcal{C}}_f$ passe aussi par le point de coordonnées $\left(1;a\right)$ car $f\left(1\right)=a$.

VII- Représentation graphique de quelques fonctions usuelles

7-3/ La fonction $x\mapsto a{x}^3 \left(a\in \mathrm{ℝ}\right)$

Applications

1. Dresser le tableau de variations de chacune des fonctions suivantes puis tracer sa courbe représentative :

.$f\left(x\right)=x^3 ; g\left(x\right)=-\frac{1}{2}{x}^3 ; h\left(x\right)=\frac{1}{4}{x}^2\left|x\right|$

VII- Représentation graphique de quelques fonctions usuelles

7-4/ La fonction $x\mapsto \sqrt{x+a} \left(a\in \mathrm{ℝ}\right)$

Soit $f$ la fonction définie par $f\left(x\right)=\sqrt{x+a}$ où $a$ est un nombre réel.

La fonction $f$ est définie et strictement croissante sur l'intervalle $[-a;+\infty [$.

• Tableaux de variations :

• Courbes représentatives :

VII- Représentation graphique de quelques fonctions usuelles

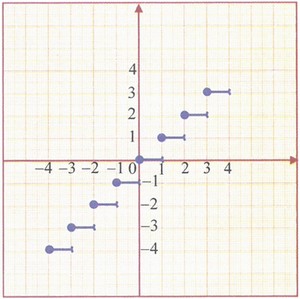
7-5/ La fonction partie entière

Définition

Soit $x$ un nombre réel.

La partie entière de $x$ est le plus grand entier relatif $n$ qui est inférieur ou égal à $x$.

On la note $E\left(x\right)$ ou $\left[x\right]$.

VII- Représentation graphique de quelques fonctions usuelles

7-5/ La fonction partie entière

Applications

1. Déterminer la partie entière de chacun des nombres suivants :

$\frac{17}{3} ; -\frac{2020}{19} ; -2018 ; \frac{24}{25} ; \frac{\mathrm{\pi }}{2} ; \frac{n}{n+1} ; \frac{n+1}{n} ; \sqrt{n+1}-\sqrt{n}$

VII- Représentation graphique de quelques fonctions usuelles

7-5/ La fonction partie entière

Proposition

Pour tout $x\in \mathrm{ℝ}$ : $E\left(x\right)\le x<E\left(x\right)+1$ et $x-1<E\left(x\right)\le x$

Pour tout $x\in \mathrm{ℝ}$ : $E\left(x\right)=x\iff x\in \mathrm{\mathbb{Z}}$

Pour tout $x\in \mathrm{ℝ}$ et pour tout $n\in \mathrm{\mathbb{Z}}$ : $E\left(n+x\right)=E\left(x\right)+n$

VII- Représentation graphique de quelques fonctions usuelles

7-5/ La fonction partie entière

Applications

1. Résoudre dans $\mathrm{ℝ}$ les équations et les inéquations suivantes :

On considère la fonction numérique $f$ définie sur $\mathrm{ℝ}$ par : $f\left(x\right)=x-E\left(x\right)$

2. Calculer : $f\left(-5\right) ; f\left(\sqrt{2}\right) ; f\left(8\right) ; f\left(\frac{3}{2}\right) ; f\left(5,2\right)$

3. Montrer que : $\left(\forall x\in \mathrm{ℝ}\right) 0\le f\left(x\right)<1$

4. Tracer la courbe représentative de $f$ sur l'intervalle $\left[-6;6\right]$.

IIX- Composée de deux fonctions numériques

Définition

Soit $f$ et $g$ deux fonctions définies respectivement sur deux ensembles $I$ et $J$ tels que : $f\left(I\right)\subset J$

La fonction numérique $h$ définie sur $I$ par $h\left(x\right)=g\left(f\left(x\right)\right)$ est appelée composée des fonctions $f$ et $g$ dans cet ordre.

Elle est notée $g\circ f$ (se lit : $g$ rond $f$).

On a alors : $\left(\forall x\in I\right) g\circ f\left(x\right)=g\left(f\left(x\right)\right)$

IIX- Composée de deux fonctions numériques

Remarques

- On n'a pas en général : $g\circ f=f\circ g$

- On a $D_{g\circ f}=\left\{x\in \mathrm{ℝ}/x\in D_f et f\left(x\right)\in D_g\right\}$ et $D_{f\circ g}=\left\{x\in \mathrm{ℝ}/x\in D_g et g\left(x\right)\in D_f\right\}$.

- Pour décomposer une fonction, les conventions de priorité de calcul (entre puissance, produit, somme, ....) permettent de déterminer les fonctions de référence et l'ordre dans lequel les enchaîner.

IIX- Composée de deux fonctions numériques

Applications

1. Définir les fonctions $f\circ g$ et $g\circ f$ dans chacun des cas suivants :

$$\begin{gathered} \boxed{1} f\left(x\right)=x^2 et g\left(x\right)=\frac{2x-1}{x-1} \\ \boxed{2} f\left(x\right)=2x-1 et g\left(x\right)=\frac{x-1}{x+1} \\ \boxed{3} f\left(x\right)=x^2+2 et g\left(x\right)=\sqrt{x} \\ \boxed{4} f\left(x\right)=\sqrt{x^2-1} et g\left(x\right)=\frac{1}{x^2-x} \end{gathered}$$

2. Décomposer la fonction $f$ en deux fonctions dans chacun des cas suivants :

$$\begin{gathered} \boxed{1} f\left(x\right)={\left(x-1\right)}^3 \\ \boxed{2} f\left(x\right)=\sqrt{2-5x} \\ \boxed{3} f\left(x\right)=3-\frac{1}{{\left(2x-1\right)}^2} \end{gathered}$$

IIX- Composée de deux fonctions numériques

Proposition

Soit $f$ et $g$ deux fonctions définies respectivement sur deux ensembles $I$ et $J$ tels que : $f\left(I\right)\subset J$

Si $f$ et $g$ ont le même sens de variation, alors $g\circ f$ est croissante (éventuellement strictement croissante) sur l'intervalle $I$.

Si $f$ et $g$ ont des sens de variation contraires, alors $g\circ f$ est décroissante (éventuellement strictement décroissante) sur l'intervalle $I$.

IIX- Composée de deux fonctions numériques

Applications

1. En utilisant la propriété de la monotonie de la composée de deux fonctions, étudier la monotonie de la fonction $f$ sur l’intervalle $I$ dans chacun des cas suivants :

Soit $f$ la fonction numérique définie sur $\mathrm{ℝ}$ par : $f\left(x\right)=\frac{x^2-2x+2}{2x^2-4x+3}$

2. Montrer que : $\left(\forall x\in \mathrm{ℝ}\right) \frac{1}{2}<f\left(x\right)\le 1$

On considère les fonctions numériques $u$ et $v$ définies par $u\left(x\right)=x^2-2x$ et $v\left(x\right)=\frac{x+2}{2x+3}$.

3. Donner le tableau de variations de chacune des fonctions $u$ et $v$.

4. En utilisant les variations des fonctions n et v, étudier les variations de la fonction $f$ sur chacun des intervalles $[1;+\infty [$ et $]-\infty ;1]$.

IX- Fonction périodique

Définition

Soit $f$ une fonction numérique et $D_f$ son ensemble de définition.

On dit que $f$ est périodique s’il existe un réel non nul $T$ tel que pour tout $x\in D_f$ :

$\left(x+T\right)\in D_f$ et $\left(x-T\right)\in D_f$ et $f\left(x+T\right)=f\left(x\right)$

Le nombre réel $T$ est appelé alors une période de $f$.

La plus petite période strictement positive de la fonction $f$ (lorsqu’elle existe) est appelée la période de la fonction $f$.

IX- Fonction périodique

Applications

Soit $a$ un réel strictement positif.

1. Montrer que la fonction $x\mapsto \tan \left(ax\right)$ est périodique et donner sa période.

2. Déterminer la période de chacune des fonctions suivantes :

$$\begin{gathered} f_1 : x\mapsto {\cos }^{2}x \\ {f}_2 : x\mapsto \sin \left(\frac{x}{2}-\frac{\mathrm{\pi }}{3}\right) \\ {f}_3 : x\mapsto \sin \left(3x\right)+\cos \left(2x\right) \\ {f}_4 : x\mapsto \tan \left(3x\right)-\cos \left(4x\right) \end{gathered}$$

3. Montrer que la fonction $x\mapsto x-E\left(x\right)$ est périodique de période égale à $1$.

IX- Fonction périodique

Proposition

Soit $f$ une fonction périodique de période $T$ et ${\mathcal{C}}_f$ sa courbe représentative dans un repère $\left(O;\overrightarrow{i};\overrightarrow{j}\right)$.

Pour tout $k\in \mathrm{\mathbb{Z}}*$, le nombre $kT$ est aussi une période de la fonction $f$.

La courbe de ${\mathcal{C}}_f$ est invariante par toute translation de vecteur $kT.\overrightarrow{i}$ avec $k\in \mathrm{\mathbb{Z}}$.

Si $x_0\in \mathrm{ℝ}$ est un réel donné, la courbe représentative ${\mathcal{C}}_f$ est la réunion des images de l’ensemble $\left\{M\left(x;f\left(x\right)\right)/x\in D_f\cap [x_0;x_0+T[\right\}$ par toutes les translations de vecteur $kT.\overrightarrow{i}$ avec $k\in \mathrm{\mathbb{Z}}$.

Ainsi, pour étudier une fonction périodique de période $T$, il suffit de l’étudier sur un intervalle de $\mathrm{ℝ}$ de longueur $T$. (Très souvent, on choisit un des deux intervalles $[0;T[$ ou $[-\frac{T}{2};\frac{T}{2}[$).

IX- Fonction périodique

Applications

On considère la fonction $f$ définie sur $\mathrm{ℝ}$, périodique de période $T=3$ et telle que $\left(\forall x\in \left[0;3\right]\right) f\left(x\right)=\left|x-2\right|$.

1. Représenter graphiquement la fonction $f$ sur l'intervalle $I=\left[-6;9\right]$.

2. Calculer : $f\left(9,78\right) ; f\left(-8,75\right) ; f\left(2020\right)$

Pour tout $k\in \mathrm{\mathbb{Z}}$, on pose : $I_k=[3k;3\left(k+1\right)[$

3. Calculer $f\left(x\right)$ en fonction de $x$ et $k$ lorsque $x\in I_k$.