Séance 4-1-1 : Généralités sur les fonctions - Partie 1 (Cours)

Sommaire

I- Ensemble de définition - parité d’une fonction

1-1/ Ensemble de définition d'une fonction numérique

1-2/ Parité d'une fonction numérique

II- Monotonie d'une fonction numérique

2-1/ Sens de variations d'une fonction (Rappels)

2-2/ Monotonie et parité

2-3/ Variations des fonctions $f+\lambda$ et $\lambda f$

III- Comparaison de deux fonctions numériques

3-1/ Fonction positive - fonction négative

3-2/ Comparaison de deux fonctions numériques

IV- Fonction majorée - fonction minorée - fonction bornée

V- Extremums d’une fonction numérique

I- Ensemble de définition - parité d’une fonction

1-1/ Ensemble de définition d'une fonction numérique

Définition

Soit $A$ une partie de $\mathrm{ℝ}$.

Une fonction $f$ définie d'un ensemble $A$ dans $\mathrm{ℝ}$ est la donnée pour chaque élément de $A$ d'un unique élément $y$ de $\mathrm{ℝ}$ appelé image de $x$.

On note alors $y=f\left(x\right)$.

L'ensemble $A$ des nombres réels qui possèdent une image par $f$, est appelé ensemble de définition de la fonction numérique $f$.

Il est noté traditionnellement $D_f$.

I- Ensemble de définition - parité d’une fonction

1-1/ Ensemble de définition d'une fonction numérique

Remarque

L’ensemble de définition d'une fonction $f$ est la plus grande partie de $\mathrm{ℝ}$ sur laquelle on peut calculer la valeur de $f\left(x_0\right)$ en tout point $x_0$ de cette partie.

On a donc : $D_f=\left\{x\in \mathrm{ℝ}/f\left(x\right)\in \mathrm{ℝ}\right\}$

En pratique, on utilise souvent l’équivalence : $x\in D_f\iff \left(x\in \mathrm{ℝ} et f\left(x\right)\in \mathrm{ℝ}\right)$

I- Ensemble de définition - parité d’une fonction

1-1/ Ensemble de définition d'une fonction numérique

Applications

1. Déterminer l’ensemble de définition de la fonction / dans chacun des cas suivants :

I- Ensemble de définition - parité d’une fonction

1-2/ Parité d'une fonction numérique

Définition

Soit $f$ une fonction numérique et $D_f$ son ensemble de définition.

- On dit que la fonction $f$ est paire si pour tout $x\in D_f$ : $-x\in D_f$ et $f\left(-x\right)=f\left(x\right)$

- On dit que la fonction $f$ est impaire si pour tout $x\in D_f$ : $-x\in D_f$ et $f\left(-x\right)=-f\left(x\right)$

I- Ensemble de définition - parité d’une fonction

1-2/ Parité d'une fonction numérique

Proposition

Si $f$ est une fonction paire, alors l'axe des ordonnées est un axe de symétrie de sa courbe ${\mathcal{C}}_f$.

Si $f$ est une fonction impaire, alors l'origine du repère est un centre de symétrie de sa courbe ${\mathcal{C}}_f$.

I- Ensemble de définition - parité d’une fonction

1-2/ Parité d'une fonction numérique

Applications

1. Étudier la parité de la fonction $f$ dans chacun des cas suivants :

II- Monotonie d'une fonction numérique

2-1/ Sens de variations d'une fonction (Rappels)

Définition

Soit $f$ une fonction numérique définie sur un intervalle $I$ inclus dans son ensemble de définition.

On dit que la fonction $f$ est croissante sur $I$ si ;

$\left(\forall \left(x_1;x_2\right)\in I^2\right) \left(x_1\le x_2\Rightarrow f\left(x_1\right)\le f\left(x_2\right)\right)$

On dit que la fonction $f$ est strictement croissante sur $I$ si :

$\left(\forall \left(x_1;x_2\right)\in I^2\right) \left(x_1<x_2\Rightarrow f\left(x_1\right)<f\left(x_2\right)\right)$

On dit que la fonction $f$ est décroissante sur $I$ si :

$\left(\forall \left(x_1;x_2\right)\in I^2\right) \left(x_1\le x_2\Rightarrow f\left(x_1\right)\ge f\left(x_2\right)\right)$

On dit que la fonction $f$ est strictement décroissante sur $I$ si :

$\left(\forall \left(x_1;x_2\right)\in I^2\right) \left(x_1<x_2\Rightarrow f\left(x_1\right)>f\left(x_2\right)\right)$

II- Monotonie d'une fonction numérique

2-1/ Sens de variations d'une fonction (Rappels)

Proposition

Soit $f$ une fonction numérique définie sur un intervalle $I$, et $x_1$ et $x_2$ deux éléments distincts de $I$.

Le nombre $T\left(x_1;x_2\right)=\frac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}$ est appelé taux de variation (ou d'accroissement) de la fonction $f$ entre $x_1$ et $x_2$. De plus, on a les propriétés suivantes :

- $f$ est croissante sur $I$ si, et seulement si : $\left(\forall \left(x_1;x_2\right)\in I^2\right) \left(x_1\ne x_2\Rightarrow T\left(x_1;x_2\right)\ge 0\right)$

- $f$ est strictement croissante sur $I$ si, et seulement si : $\left(\forall \left(x_1;x_2\right)\in I^2\right) \left(x_1\ne x_2\Rightarrow T\left(x_1;x_2\right)>0\right)$

- $f$ est décroissante sur $I$ si, et seulement si : $\left(\forall \left(x_1;x_2\right)\in I^2\right) \left(x_1\ne x_2\Rightarrow T\left(x_1;x_2\right)\le 0\right)$

- $f$ est strictement décroissante sur $I$ si, et seulement si : $\left(\forall \left(x_1;x_2\right)\in I^2\right) \left(x_1\ne x_2\Rightarrow T\left(x_1;x_2\right)<0\right)$

II- Monotonie d'une fonction numérique

2-1/ Sens de variations d'une fonction (Rappels)

Applications

1. Étudier les variations de la fonction numérique $f$ sur les intervalles $I$ et $J$ dans les deux cas suivants :

$$\begin{gathered} \boxed{1} f\left(x\right)=\frac{2x-3}{x+1} ; I=]-1;+\infty [ ; J=]-\infty ;-1[ \\ \boxed{2} f\left(x\right)=\sqrt{x^2-4x+3} ; I=]-\infty ;1] ; J=[3;+\infty [ \end{gathered}$$

II- Monotonie d'une fonction numérique

2-2/ Monotonie et parité

Proposition

Soit $f$ une fonction numérique d’ensemble de définition $D_f$ symétrique par rapport à $0$ (c’est-à-dire que pour tout $x\in D_f$ : $-x\in D_f$) .

Pour tout intervalle $I$ inclus dans ${\mathrm{ℝ}}^{+}\cap D_f$, on pose : $I\text{'}=\left\{-x/x\in I\right\}$

Alors :

- Si la fonction $f$ est paire, alors les sens de monotonie sur $I$ et $I\text{'}$ sont opposés.

- Si la fonction $f$ est impaire, alors les sens de monotonie sur $I$ et $I\text{'}$ sont identiques.

II- Monotonie d'une fonction numérique

2-2/ Monotonie et parité

Applications

Soit $f$ la fonction numérique définie sur $\mathrm{ℝ}*$ par : $f\left(x\right)=x+\frac{2}{x}$

1. Étudier la parité de!a fonction $f$.

2. Étudier la monotonie de la fonction $f$ sur chacun des intervalles $]0;\sqrt{2}]$ et $[\sqrt{2};+\infty [$.

3. En déduire la monotonie de la fonction $f$ sur chacun des intervalles $[-\sqrt{2};0[$ et $]-\infty ;-\sqrt{2}]$.

Soit $g$ la fonction numérique définie sur $\mathrm{ℝ}$ par : $g\left(x\right)=\frac{\left|x\right|}{x^2+\left|x\right|+1}$

4. Étudier la parité de la fonction $g$.

5. Étudier la monotonie de la fonction $g$ sur ${\mathrm{ℝ}}^{+}$.

6. En déduire la monotonie de la fonction $g$ sur ${\mathrm{ℝ}}^{-}$, puis dresser son tableau de variations.

Soit $h$ la fonction numérique définie sur $\mathrm{ℝ}$ par : $h\left(x\right)=x+\left|2x-3\right|-\left|2x+3\right|$

7. Montrer que la fonction $h$ est impaire.

8. Étudier la monotonie de la fonction $h$ sur chacun des intervalles $[0;\frac{3}{2}]$ et $[\frac{3}{2};+\infty [$.

9. Dresser le tableau de variations de la fonction $h$.

10. Tracer la courbe ${\mathcal{C}}_h$ de la fonction $h$ dans un repère orthonormé.

II- Monotonie d'une fonction numérique

2-3/ Variations des fonctions $f+\lambda$ et $\lambda f$

Proposition

Soit $f$ une fonction numérique définie sur un intervalle $I$, et $\lambda$ un nombre réel non nul.

- Les fonctions $f$ et $f+\lambda$ ont le même sens de variation sur l'intervalle $I$.

- Si $\lambda >0$ alors les fonctions $f$ et $\lambda f$ ont le même sens de variation sur l'intervalle $I$.

- Si $\lambda <0$ alors les fonctions $f$ et $\lambda f$ ont des sens de variation opposés sur l'intervalle $I$.

II- Monotonie d'une fonction numérique

2-3/ Variations des fonctions $f+\lambda$ et $\lambda f$

Applications

1. Étudier la monotonie de la fonction $f$ sur l'intervalle $I$ dans chacun des cas suivants :

$$\begin{gathered} \boxed{1} f\left(x\right)=2\sqrt{x}-3 et I={\mathrm{ℝ}}^{+} \\ \boxed{2} f\left(x\right)=x^2-5 et I={\mathrm{ℝ}}^{-} \\ \boxed{3} f\left(x\right)=\frac{x+1}{x} et I=]0;+\infty [ \\ \boxed{4} f\left(x\right)=\frac{14x-10}{x} et I=]-\infty ;0[ \end{gathered}$$

III- Comparaison de deux fonctions numériques

3-1/ Fonction positive - fonction négative

Définition

Soit $f$ une fonction numérique d’ensemble de définition $D_f$.

- On dit que la fonction $f$ est positive sur $D_f$ si $\left(\forall x\in D_f\right) f\left(x\right)\ge 0$, et on écrit : $f\ge 0$

- On dit que la fonction $f$ est négative sur $D_f$ si $\left(\forall x\in D_f\right) f\left(x\right)\le 0$, et on écrit : $f\le 0$

III- Comparaison de deux fonctions numériques

3-1/ Fonction positive - fonction négative

Applications

1. Étudier le signe de la fonction f dans chacun des cas suivants :

$$\begin{gathered} \boxed{1} f\left(x\right)=\frac{3x+2}{-2x^2+x+1} \\ \boxed{2} f\left(x\right)=\frac{x^2+x-6}{2x+1} \\ \boxed{3} f\left(x\right)=\left(x^2+x+1\right)\left(\sqrt{x+1}-1\right) \end{gathered}$$

III- Comparaison de deux fonctions numériques

3-2/ Comparaison de deux fonctions numériques

Définition

Soit $f$ et $g$ deux fonctions numériques définies sur un même ensemble $D$.

On dit que $f$ est inférieure ou égale à $g$ sur $D$ (ou que $g$ est supérieure ou égale à $f$ sur $D$) si :

$\left(\forall x\in D\right) f\left(x\right)\le g\left(x\right)$

On écrit : $f\le g$ sur $D$.

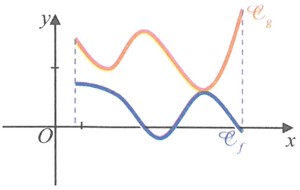
III- Comparaison de deux fonctions numériques

3-2/ Comparaison de deux fonctions numériques

Applications

1. Comparer les fonctions $f$ et $g$ dans chacun des cas suivants :

$$\begin{gathered} \boxed{1} f\left(x\right)=x et g\left(x\right)=\frac{1}{x} \\ \boxed{2} f\left(x\right)=\frac{x}{x+1} et g\left(x\right)=x^2 \\ \boxed{3} f\left(x\right)=\frac{1+2x}{1+4x} et g\left(x\right)=\frac{1-4x}{1-2x} \\ \boxed{4} f\left(x\right)=\sqrt{x^2+4} et g\left(x\right)=x+2 \end{gathered}$$

IV- Fonction majorée - fonction minorée - fonction bornée

Définition

Soit $f$ une fonction numérique et $D_f$ son ensemble de définition.

- On dit que la fonction $f$ est majorée s'il existe un réel $M$ tel que : $\left(\forall x\in D_f\right) f\left(x\right)\le M$

Le nombre $M$ est dit un majorant de la fonction $f$.

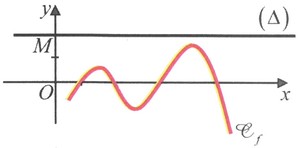
- On dit que la fonction $f$ est minorée s’il existe un réel $m$ tel que : $\left(\forall x\in D_f\right) f\left(x\right)\ge m$

Le nombre $m$ est dit un minorant de la fonction $f$.

- On dit que la fonction $f$ est bornée si elle à la fois majorée et minorée, c’est-à-dire qu’il existe deux réels $m$ et $M$ tels que : $\left(\forall x\in D_f\right) m\le f\left(x\right)\le M$

IV- Fonction majorée - fonction minorée - fonction bornée

Proposition

Soit $f$ une fonction numérique et $D_f$ son ensemble de définition.

Pour que la fonction $f$ soit bornée, il faut et il suffit que :

$\left(\exists \alpha \in {\mathrm{ℝ}}^{+}\right) \left(\forall x\in D_f\right) \left|f\left(x\right)\right|\le \alpha$

IV- Fonction majorée - fonction minorée - fonction bornée

Applications

On considère la fonction numérique $f$ définie sur $\mathrm{ℝ}$ par : $f\left(x\right)=\frac{2x^2+7x+7}{x^2+3x+3}$

1)Montrer que la fonction $f$ est majorée par $\frac{7}{3}$.

2)Montrer que la fonction $f$ est minorée par $1$.

Soit g la fonction numérique définie sur $\mathrm{ℝ}*$ par : $g\left(x\right)=x+\frac{1}{x}$

3. Montrer que la fonction $g$ est majorée par $2$ sur ${\mathrm{ℝ}}_{+}^{*}$.

4. En déduire que la fonction $g$ est minorée par $-2$ sur ${\mathrm{ℝ}}_{-}^{*}$.

Soit $u$ et $v$ les fonctions définies sur $\mathrm{ℝ}$ par $u\left(x\right)=\frac{x^4-x^2}{x^4+1}$ et $v\left(x\right)=2\cos x-7\sin \left(2x\right)+3$

5. Montrer que les fonctions $u$ et $v$ sont bornées sur $\mathrm{ℝ}$.

On considère la fonction numérique $w$ définie sur $\mathrm{ℝ}*$ par : $w\left(x\right)=x-\sqrt{x+1}$

6. Montrer par l'absurde que la fonction $w$ n'est pas majorée sur ${\mathrm{ℝ}}^{+}$.

V- Extremums d’une fonction numérique

Définition

Soit $f$ une fonction numérique, $D_f$ son ensemble de définition et $x_0\in D_f$.

- On dit que $f\left(x_0\right)$ est la valeur maximale absolue (ou le maximum absolu) de la fonction $f$ si :

$\left(\forall x\in D_f\right) f\left(x\right)\le f\left(x_0\right)$

- On dit que $f\left(x_0\right)$ est une valeur maximale relative de la fonction $f$ s’il existe un intervalle ouvert $I$ centré en $x_0$ et inclus dans $D_f$ tel que :

$\left(\forall x\in I\right) f\left(x\right)\le f\left(x_0\right)$

- On dit que $f\left(x_0\right)$ est la valeur minimale absolue (ou le minimum absolu) de la fonction $f$ si :

$\left(\forall x\in D_f\right) f\left(x\right)\ge f\left(x_0\right)$

- On dit que $f\left(x_0\right)$ est une valeur minimale relative de la fonction / s'il existe un intervalle ouvert $I$ centré en $x_0$ et inclus dans $D_f$ tel que :

$\left(\forall x\in I\right) f\left(x\right)\ge f\left(x_0\right)$

- Les valeurs minimales et maximales de la fonction $f$ sont appelées les extremums de $f$.

V- Extremums d’une fonction numérique

Remarques

Ne jamais confondre minorant et minimum d'une fonction. Le minimum d'une fonction est un minorant qui admet un antécédent.

Autrement dit, le réel $m$ est une valeur minimale de $f$ sur $I$ si, et seulement si :

$\left\{\begin{array}{l}\left(\forall x\in I\right) f\left(x\right)\ge m\\ \left(\exists x_0\in I\right) f\left(x_0\right)=m\end{array}\right.$

Ne jamais confondre majorant et maximum d’une fonction. Le maximum d'une fonction est un majorant qui admet un antécédent.

Autrement dit, le réel M est une valeur maximale de $f$ sur $I$ si, et seulement si :

$\left\{\begin{array}{l}\left(\forall x\in I\right) f\left(x\right)\le M\\ \left(\exists x_0\in I\right) f\left(x_0\right)=M\end{array}\right.$

V- Extremums d’une fonction numérique

Applications

On considère les fonctions $f$ et $g$ définies sur $\mathrm{ℝ}$ par $f\left(x\right)=x^2+2x+3$ et $g\left(x\right)=-x^2+3x+5$.

1. Montrer que $2$ est la valeur minimale absolue de la fonction $f$.

2. Montrer que $\frac{29}{4}$ est la valeur maximale absolue de la fonction $g$.

On considère la fonction $h$ définie sur $\mathrm{ℝ}*$ par $h\left(x\right)=\left|x\right|+\frac{1}{\left|x\right|}$.

3. Montrer que $h$ admet un minimum absolu au point $1$.