Séance 2-1 : Ensembles (Cours)

Sommaire

I- Généralités sur les ensembles

1-1/ Notion d'ensemble - élément d'un ensemble

1-2/ Définition d'un ensemble

1-3/ Égalité de deux ensembles

II- Parties d'un ensemble - Inclusion - Complémentaire

2-1/ Inclusion

2-2/ Complémentaire

2-3/ Ensemble des parties d’un ensemble

III- Opérations dans $\mathcal{P}\left(E\right)$

3-1/ Intersection

3-2/ Réunion

3-3/ Règles de calcul

3-4/ Différence de deux ensembles

3-5/ Produit cartésien

I- Généralités sur les ensembles

1-1/ Notion d'ensemble - élément d'un ensemble

Définition

Un ensemble $E$ est une collection d'objets satisfaisant un certain nombre de propriétés et chacun de ces objets est appelé élément de cet ensemble.

Si $x$ est un élément de l'ensemble $E$, on dit que $x$ appartient à $E$ et on note $x\in E$.

Si $x$ n'appartient pas à $E$, on note $x\notin E$.

I- Généralités sur les ensembles

1-2/ Définition d'un ensemble

Il y a deux manières de définir un ensemble E :

• En extension :

On énumère tous les éléments de $E$, c'est-à-dire en donnant la liste de ses éléments, s'il possède un nombre fini d'éléments (pas trop grand).

Dans ce cas, l'ordre dans lequel on donne les éléments n'a aucune importance.

• En compréhension :

On décrit l'ensemble $E$ en donnant une propriété qui caractérise ses éléments.

Si $P\left(x\right)$ est la propriété qui caractérise les éléments de $E$, alors on écrit : $E=\left\{x/P\left(x\right)\right\}$

I- Généralités sur les ensembles

1-2/ Définition d'un ensemble

Applications

1. Écrire en extension les ensembles suivants :

2. Écrire en compréhension les ensembles suivants :

$$\begin{gathered} G=\left\{3;6;9;12;15\right\} \\ H=\left\{1;3;9;27;81;..\right\} \\ J=\left\{...;-8;-3;2;7;12;...\right\} \\ K=\left\{1;-\frac{1}{2};\frac{1}{4};-\frac{1}{8};\frac{1}{16};...\right\} \\ L=\left\{...;\frac{1}{9};\frac{1}{3};1;3;9;...\right\} \end{gathered}$$

I- Généralités sur les ensembles

1-3/ Égalité de deux ensembles

Définition

Soit $E$ et $F$ deux ensembles.

On dit que E et F sont égaux lorsqu'ils ont les mêmes éléments, et on écrit $E=F$.

I- Généralités sur les ensembles

1-3/ Égalité de deux ensembles

Applications

On considère l’ensemble : $E=\left\{x\in \mathrm{ℝ}/-\frac{1}{4}<\frac{x}{x^2+4}<\frac{1}{4}\right\}$

1. Montrer que : $E=\mathrm{ℝ}$

On considère les deux ensembles $A=]-\infty ;-1[$ et $B=\left\{x\in \mathrm{ℝ}/\frac{x}{x+1}>1\right\}$.

2. Montrer que : $A=B$

II- Parties d'un ensemble - Inclusion - Complémentaire

2-1/ Inclusion

Définition

Soit $A$ et $B$ deux parties d'un ensemble $E$.

On dit que $A$ est incluse dans $B$ si chaque élément de $A$ est un élément de $B$.

On note $A\subset B$.

On dit aussi que la partie $A$ est contenue dans $B$ ou que $A$ est un sous-ensemble de $B$.

En d'autres termes : $A\subset B\iff \left[\left(\forall x\in E\right); x\in A\Rightarrow x\in B\right]$

II- Parties d'un ensemble - Inclusion - Complémentaire

2-1/ Inclusion

Remarques

Soit $A$ et $B$ deux parties d'un ensemble $E$.

Dire que $A$ n'est pas inclue dans $B$ signifie qu 'il existe au moins un élément $x\in A$ tel que $x\notin B$, et on écrit $A\subseteq B$.

Pour tout ensemble $A$, on a toujours $\varnothing \subset A$ et $A\subset A$.

II- Parties d'un ensemble - Inclusion - Complémentaire

2-1/ Inclusion

Proposition

Soit $A$, $B$ et $C$ trois parties d'un ensemble E.

Si $A\subset B$ et $B\subset C$, alors $A\subset C$.

$A=B$ si, et seulement si $A\subset B$ et $B\subset A$.

II- Parties d'un ensemble - Inclusion - Complémentaire

2-1/ Inclusion

Remarques

- L'écriture $A\ne B$ signifie que les ensembles $A$ et $B$ sont distincts.

- $A=B\iff \left[\left(\forall x\in E\right); x\in A\iff x\in B\right]$

- Si $A\subset B$ et $B\subset C$, alors on peut écrire $A\subset B\subset C$. Par exemple : $\mathrm{\mathbb{N}}\subset \mathrm{\mathbb{Z}}\subset \mathrm{ℝ}$

II- Parties d'un ensemble - Inclusion - Complémentaire

2-2/ Complémentaire

Définition

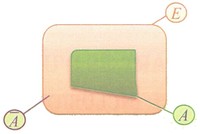
Soit $A$ une partie d'un ensemble $E$.

L’ensemble des éléments de $E$ n'appartenant pas à l'ensemble $A$ est appelé le complémentaire de $A$ dans $E$.

On le note $C_E^A$ ou $\overline{A}$.

On a alors : $C_E^A=\left\{x\in E/x\notin A\right\}$ et $x\in \overline{A}\iff x\notin A$

II- Parties d'un ensemble - Inclusion - Complémentaire

2-2/ Complémentaire

Applications

On considère l'ensemble : $A=\left\{x\in \mathrm{\mathbb{N}}/x^2-4x>0\right\}$

1. Décrire en extension l'ensemble $C_{\mathrm{\mathbb{N}}}^A$.

On considère l'ensemble suivant : $B=\left\{x\in \mathrm{ℝ}/x^2+x<5\right\}$

2. Montrer que : $[2;+\infty [\subset C_{\mathrm{ℝ}}^B$

On considère l'ensemble : $E=\left\{x\in \mathrm{ℝ}/x^4+x^3+x^2+x=2\right\}$

3. Montrer que : $[1;+\infty [\subset C_{\mathrm{ℝ}}^E$

II- Parties d'un ensemble - Inclusion - Complémentaire

2-2/ Complémentaire

Proposition

Soit $A$ et $B$ deux parties d'un ensemble $E$.

Alors :

- $C_E^E=\varnothing$ et $C_E^{\varnothing }=E$ et $C_E^{\overline{A}}=A$

- $A\subset B\iff \overline{B}\subset \overline{A}$

II- Parties d'un ensemble - Inclusion - Complémentaire

2-3/ Ensemble des parties d’un ensemble

Définition

Soit $E$ un ensemble.

On appelle ensemble des parties de $E$, et on note $\mathcal{P}\left(E\right)$, l'ensemble des sous-ensembles de $E$.

En d'autres termes : $A\in \mathcal{P}\left(E\right)\iff A\subset E$

II- Parties d'un ensemble - Inclusion - Complémentaire

2-3/ Ensemble des parties d’un ensemble

Remarques

Les éléments de $\mathcal{P}\left(E\right)$ sont des ensembles. En particulier, on a $\varnothing \in \mathcal{P}\left(E\right)$ et $E\in \mathcal{P}\left(E\right)$.

Si $E$ est un ensemble non vide, alors : $a\in E\iff \left\{a\right\}\in \mathcal{P}\left(E\right)$

III- Opérations dans $\mathcal{P}\left(E\right)$

3-1/ Intersection

Définition

Soit $A$ et $B$ deux parties d'un ensemble $E$.

L'intersection des ensembles $A$ et $B$, notée $A\cap B$, est l'ensemble des éléments de $E$ qui sont dans $A$ et dans $B$.

En d'autres termes : $x\in A\cap B\iff \left(x\in A et x\in B\right)$

On a alors : $A\cap B=\left\{x\in E/x\in A et x\in B\right\}$

III- Opérations dans $\mathcal{P}\left(E\right)$

3-1/ Intersection

Proposition

Soit $A$, $B$ et $C$ trois parties d'un ensemble $E$.

On a alors les propriétés suivantes :

III- Opérations dans $\mathcal{P}\left(E\right)$

3-2/ Réunion

Définition

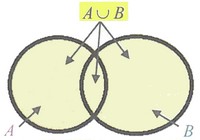
Soit $A$ et $B$ deux parties d'un ensemble $E$.

La réunion des ensembles $A$ et $B$, notée $A\cup B$, est l'ensemble des éléments de $E$ qui sont dans $A$ ou dans $B$.

En d'autres termes : $x\in A\cup B\iff \left(x\in A ou x\in B\right)$

On a alors : $A\cup B=\left\{x\in E/x\in A ou x\in B\right\}$

III- Opérations dans $\mathcal{P}\left(E\right)$

3-2/ Réunion

Proposition

Soit $A$, $B$ et $C$ trois parties d'un ensemble $E$.

On a alors les propriétés suivantes :

III- Opérations dans $\mathcal{P}\left(E\right)$

3-3/ Règles de calcul

Proposition

Soit $A$, $B$ et $C$ trois parties d'un ensemble $E$.

On a alors les propriétés suivantes :

Distributivité de la réunion par rapport à l'intersection :

$A\cup \left(B\cap C\right)=\left(A\cup B\right)\cap \left(A\cup C\right)$

Distributivité de la réunion par rapport à l'intersection :

$A\cap \left(B\cup C\right)=\left(A\cap B\right)\cup \left(A\cap C\right)$

III- Opérations dans $\mathcal{P}\left(E\right)$

3-3/ Règles de calcul

Proposition

Soit $A$, $B$ et $C$ trois parties d'un ensemble $E$.

Alors : $\overline{A\cap B}=\overline{A}\cup \overline{B}$ et $\overline{A\cup B}=\overline{A}\cap \overline{B}$

Ces deux égalités sont appelées « Lois de Morgan ».

III- Opérations dans $\mathcal{P}\left(E\right)$

3-3/ Règles de calcul

Applications

On considère les deux ensembles $A$ et $B$ définis par :

$A=\left\{\frac{\mathrm{\pi }}{6}+\frac{k\mathrm{\pi }}{3}/k\in \mathrm{\mathbb{Z}}\right\}$ et $B=\left\{-\frac{\mathrm{\pi }}{4}+\frac{k\mathrm{\pi }}{3}/k\in \mathrm{\mathbb{Z}}\right\}$

1. Montrer que : $A\cap B=\varnothing$

2. Déterminer l’ensemble $\left(A\cup B\right)\cap \left[-\frac{\mathrm{\pi }}{2};\frac{\mathrm{\pi }}{2}\right]$.

Soit $A$, $B$ et $C$ trois parties d'un ensemble $E$.

3. Montrer que $A\cap \left(B\cup \left(A\cap C\right)\right)=A\cap \left(B\cup C\right)$ et $A\cup \left(B\cap \left(A\cup C\right)\right)=A\cup \left(B\cap C\right)$.

4. Montrer que : $\left(A\cup B\right)\cap \left(B\cup C\right)\cap \left(C\cup A\right)=\left(A\cap B\right)\cup \left(B\cap C\right)\cup \left(C\cap A\right)$

5. Simplifier $A\cap \left(\overline{B\cap C}\right)$ et $\left(A\cap \overline{B}\right)\cap \left(\overline{A\cap \overline{C}}\right)$.

III- Opérations dans $\mathcal{P}\left(E\right)$

3-4/ Différence de deux ensembles

Définition

Soit $A$ et $B$ deux parties d'un ensemble $E$.

La différence des ensembles $A$ et $B$ dans cet ordre, notée $A\backslash B$, est l'ensemble des éléments de $A$ qui ne sont pas dans $B$.

En d'autres termes : $x\in A\backslash B\iff \left(x\in A et x\notin B\right)$

On a alors : $A\backslash B=\left\{x\in E/x\in A et x\notin B\right\}$

$A\backslash B$ se lit « $A$ moins $B$ » ou « $A$ privé de $B$ »

III- Opérations dans $\mathcal{P}\left(E\right)$

3-4/ Différence de deux ensembles

Proposition

Soit $A$ et $B$ deux parties d'un ensemble $E$.

On a alors les propriétés suivantes :

$$\begin{gathered} \boxed{1} A\backslash B=A\cap C_E^B=A\cap \overline{B} \\ \boxed{2} A=\left(A\backslash B\right)\cup \left(A\cap B\right) \end{gathered}$$

III- Opérations dans $\mathcal{P}\left(E\right)$

3-4/ Différence de deux ensembles

Applications

1. Déterminer les ensembles $A$ et $B$ sachant que :

$A\cup B=\left\{1;2;3;....;11\right\}$ et $A\cap B=\left\{4;5;6;11\right\}$ et $A\backslash B=\left\{7;8;9;10\right\}$

Soit $A$, $B$ et $C$ trois parties d'un ensemble $E$.

2. Montrer que $A\backslash \left(B\cap C\right)=\left(A\backslash B\right)\cup \left(A\backslash C\right)$ et $A\backslash \left(B\cup C\right)=\left(A\backslash B\right)\cap \left(A\backslash C\right)$.

3. Montrer que si $A\cap B=A\cap C$ et $B\backslash A=C\backslash A$, alors $B=C$.

Soit $A$, $B$, $C$ et $D$ quatre parties d'un ensemble $E$.

4. Montrer que : $\left[\left(B\backslash C\right)\subset A et \left(C\backslash D\right)\subset A\right]\Rightarrow \left(B\backslash A\right)\subset A$

Soit $A$ et $B$ deux parties d'un ensemble $E$.

On pose : $A\Delta B=\left(A\backslash B\right)\cup \left(B\backslash A\right)$

L’ensemble $A\Delta B$ s’appelle la différence symétrique des ensembles $A$ et $B$.

5. On suppose dans cette question que $A=\left\{1;2;3;5;6\right\}$ et $B=\left\{2;3;7;8;9\right\}$, déterminer $A\Delta B$ puis construire un diagramme de Venn pour schématiser cet ensemble.

6. Montrer que pour tous $A$ et $B$ de $\mathcal{P}\left(E\right)$, on a :

$$\begin{gathered} A\Delta A=\varnothing ; A\Delta E=\overline{A} ; A\Delta \varnothing =A \\ A\Delta B=\left(A\cup B\right)\backslash \left(A\cap B\right) ; A\Delta B=\overline{A}\Delta \overline{B} \end{gathered}$$

7. Montrer que pour tous $A$ et $B$ de $\mathcal{P}\left(E\right)$, on a les deux équivalences suivantes :

$A\Delta B=\varnothing \iff A=B$ et $A\Delta B=A\cap B\iff \left(A=\varnothing et B=\varnothing \right)$

Soit $A$, $B$ et $C$ trois parties d'un ensemble $E$.

8. Établir les deux égalités suivantes :

$$\begin{gathered} A\cap \left(B\Delta C\right)=\left(A\cap B\right)\Delta \left(A\cap C\right) \\ A\Delta \left(B\Delta C\right)=\left(A\Delta B\right)\Delta C \end{gathered}$$

III- Opérations dans $\mathcal{P}\left(E\right)$

3-5/ Produit cartésien

Définition

Soit $E$ et $F$ deux ensembles.

Le produit cartésien des ensembles $E$ et $F$, noté $E\times F$, est l'ensemble des couples $\left(x;y\right)$ tels que $x\in E$ et $y\in F$.

En d'autres termes : $\left(x;y\right)\in E\times F\iff \left(x\in E et y\in F\right)$

On a alors : $E\times F=\left\{\left(x;y\right)/x\in E et y\in F\right\}$

III- Opérations dans $\mathcal{P}\left(E\right)$

3-5/ Produit cartésien

Remarques

Si $E=F$, le produit cartésien $E\times E$ est noté $E^2$ et appelé le carré cartésien de $E$.

Soit $E$ et $F$ deux ensembles. Alors : $E\times F=\varnothing \iff \left(E=\varnothing et F=\varnothing \right)$

III- Opérations dans $\mathcal{P}\left(E\right)$

3-5/ Produit cartésien

Applications

On considère les deux ensembles :

$A=\left\{n\in \mathrm{\mathbb{N}}/n^2<16\right\}$ et $B=\left\{n\in \mathrm{\mathbb{N}}/\left|n-2\right|\le 1\right\}$

1. Écrire en extension l'ensemble $A\times B$, puis représenter un diagramme cartésien de cet ensemble.

2. En utilisant le raisonnement par contre-exemple, justifier que :

$\left(E\times F\right)\cup \left(G\times H\right)\ne \left(E\cup G\right)\times \left(F\cup H\right)$

3. Représenter dans un repère orthonormé les ensembles suivants :

$\left[-1;1\right]\times \left[0;2\right]$ et $[0;+\infty [\times [0;2[$

4. Déterminer les éléments de l'ensemble $\mathcal{P}\left(E\times F\right)$ avec $E=\left\{2;1\right\}$ et $F=\left\{0\right\}$.