Séance 1-1-1 : Notion de logique - Partie 1 (Cours)

Mathématiques : 1Bac SM

Séance 1-1-1 : Notion de logique - Partie 1 (Cours)

Professeur : Mr CHEDDADI Haitam

Sommaire

I- Proposition - fonction propositionnelle

II- Quantificateurs

III- Opérations sur les propositions

3-1/ Négation d'une proposition

3-2/ Disjonction de deux propositions

3-3/ Conjonction de deux propositions

3-4/ Implication de deux propositions

3-5/ Condition suffisante - condition nécessaire

3-6/ Équivalence de deux propositions

I- Proposition - fonction propositionnelle

Définition

On appelle proposition (ou assertion) tout énoncé mathématique qui a une seule signification juste ou fausse ; et ne peut être juste et faux en même temps.

Applications

La phrase : « Les nombres positifs sont des entiers naturels » est-elle une proposition ? Justifier.

Déterminer la valeur de vérité de chacune des propositions suivantes :

P : $« \frac{π}{2} \in ℚ »$

Q : $« {(\sqrt{\frac{3 + \sqrt{5}}{2}} - \sqrt{\frac{3 - \sqrt{5}}{2}})}^{2} = 1 »$

R : $« \cos \frac{π}{7} > 1 »$

S : « Les solutions de l’équation $2018 x^{2} - 2017 x - 1 = 0$ sont $1$ et $- \frac{1}{2018}$ ».

Définition

On appelle fonction propositionnelle (ou prédicat) tout énoncé mathématique contenant une variable qui appartient à un ensemble donné E et qui devient une proposition à chaque fois qu'on remplace la variable par un élément déterminé de l'ensemble E.

L'ensemble E est appelé le domaine de définition de la fonction propositionnelle.

Applications

On considère la fonction propositionnelle : $P (x; y) : « (x; y) \in ℝ^{2}; 2 x - 3 y = 7 »$

Déterminer l'ensemble des valeurs de la variable $(x; y)$ pour lesquelles $P (x; y)$ soit vraie.

Dans chacun des cas suivants, déterminer l’ensemble des nombres réels $S$ , pour que chaque fonction propositionnelle soit une proposition vraie :

A (x) : « x \in ℝ; 3 x^{2} - 2 x - 65 = 0 » C (x) : « x \in ℝ; x^{3} - 6 x + 7 = 0 » P (x) : « x \in ℝ; (2 \sin x - 1) \cos x = 0 »

B (x) : « x \in ℝ; 5 x^{2} - 2 \sqrt{15} x + 3 = 0 » D (x) : « x \in ℝ; - x^{2} + x + 6 \geq 0 » Q (x) : « x \in [- π; π]; \sin (x) \cos (x) \geq 0 »

II- Quantificateurs

Définition

Soit $P (x)$ une fonction propositionnelle d'une variable $x$ d'un ensemble non vide $E$ .

À partir de la fonction propositionnelle $« (x \in E); P (x) »$ , on définit :

- La proposition $« (\exists x \in E); P (x) »$ qui se lit « il existe au moins $x \in E$ tel que $P (x)$ », et qui est vraie lorsqu'il existe au moins $x \in E$ vérifiant la propriété $P (x)$ .

Le symbole $\exists$ s'appelle le quantificateur existentiel.

- La proposition $« (\forall x \in E); P (x) »$ qui se lit « pour toutx $x \in E$ , $P (x)$ » ou « quel que soit $x \in E$ ; $P (x)$ » et qui est vraie lorsque tous les éléments de $E$ vérifient la propriété $P (x)$ .

Le symbole $\forall$ s'appelle le quantificateur universel.

Remarques

- Dans les apparences, $« (\forall x \in E); P (x) »$ ne dépend d'aucun $x$ !

La lettre $x$ figurant dans cette proposition a le statut de variable muette. En effet, cette proposition peut aussi être écrite : $« (\forall y \in E); P (y) »$ , ou encore $« (\forall z \in E); P (z) »$ , sans en modifier le sens.

Il en est de même de la proposition $« (\exists x \in E); P (x) »$ : elle affirme qu'il existe au moins un élément $x \in E$ tel que $P (x)$ soit vraie, mais n'en définit aucun en particulier.

- Pour le quantificateur existentiel, on rencontre dans certaines énoncés $« (\exists! x \in E); P (x) »$ . L'ajout du signe $!$ derrière le symbole $\exists$ le transforme et l'énoncé devient :

« il existe un unique élément $x \in E$ tel que $P (x)$ soit vraie »

- Les quantificateurs doivent être placés avant l'assertion mathématique qu'ils quantifient.

- L'emploi de quantificateurs en guise d'abréviation au milieu d'une phrase en français est exclu : ils ne doivent figurer que dans une phrase mathématique.

- L'ordre d'écriture des quantificateurs est fondamental pour le sens d'une phrase formelle :

Quand deux quantificateurs existentiels se suivent, on peut les échanger sans changer le sens.
Quand deux quantificateurs universels se suivent, on peut les échanger sans changer le sens.
Quand on inverse l'ordre de deux quantificateurs différents, le sens change.

Applications

Déterminer la valeur de vérité de chacune des propositions suivantes :

Q_{1} : « (\exists x \in ℝ); x^{2} + x + 1 = 0 » Q_{2} : « (\exists x \in ℝ); x^{2} + x + 1 > 0 » Q_{3} : « (\exists x \in ℕ); \sqrt{x^{2} + 3} = 2 x - 4 » Q_{4} : « (\exists x \in ℝ) (\forall y \in ℝ); x \leq y »

Q_{5} : « (\exists x \in ℝ *) (\forall y \in ℤ *); x^{y} = 1 » Q_{6} : « (\forall x \in ℝ) (\exists y \in ℝ); x \leq y » Q_{7} : « (\forall x \in ℝ) (\forall y \in ℝ); x^{2} y^{2} > x y »

III- Opérations sur les propositions

3-1/ Négation d'une proposition

Définition

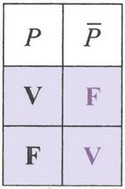
La négation d'une proposition $P$ est la proposition notée $\bar{P}$ ou $\neg P$ telle que la proposition $\bar{P}$ est vraie si la proposition $P$ est fausse et la proposition $\bar{P}$ est fausse si la proposition $P$ est vraie.

La négation est un connecteur logique unaire défini par la table de vérité :

Proposition

Soit $P (x)$ une fonction propositionnelle d'une variable $x$ d'un ensemble non vide $E$ .

La négation de la proposition $« (\forall x \in E) P (x) »$ est la proposition $« (\exists x \in E) \bar{P (x)} »$ .

La négation de la proposition $« (\exists x \in E) P (x) »$ est la proposition $« (\forall x \in E) \bar{P (x)} »$ .

Conséquence

Pour montrer que la proposition $« (\forall x \in E) P (x) »$ est fausse, il suffit de montrer que sa négation $« (\exists x \in E) \bar{P (x)} »$ est vraie.

Ce type de raisonnement est appelé raisonnement par contre-exemple.

Applications

En utilisant un raisonnement par contre-exemple, montrer que les propositions suivantes sont fausses :

P_{1} : « (\forall x \in ℝ *) x + \sqrt{x} \geq 2 » P_{3} : « (\forall x \in ℝ *) x + \frac{1}{x} \geq 2 » P_{5} : « (\forall x \in] 0; 1 [) \frac{2 x}{x^{2} (1 - x^{2})} < 1 »

P_{2} : « (\forall x \in ℝ) (\forall y \in ℝ) 2 x - 4 y \neq 5 » P_{4} : « (\forall x \in ℝ^{+}) (\forall y \in ℝ^{+}) x + y \geq \sqrt{x} + \sqrt{y} » P_{6} : « (\forall α \in] 0; 1 [) (\forall β \in] 0; 1 [) \frac{1}{α} + \frac{1}{β} < 1 - α β »

3-2/ Disjonction de deux propositions

Définition

La disjonction de deux propositions P et Q est la proposition qu'on note (P ou Q).

Elle est fausse seulement si P et Q sont toutes les deux fausses.

La disjonction est un connecteur logique binaire défini par la table de vérité :

Remarques

Les propositions $(P o u Q)$ et $(Q o u P)$ ont le même sens. On dit que la disjonction est une opération commutative.

Les propositions $[(P o u Q) o u R]$ et $[P o u (Q o u R)]$ ont le même sens. On dit que la disjonction est une opération associative.

Applications

Soit $P$ une proposition.

Montrer que la proposition $\bar{(\bar{P} o u P)}$ est fausse.

Soit $a$ et $b$ deux réels de l'intervalle $] 4; + \infty [$ , et on considère les deux équations :

$(E) : x^{2} + a x + b = 0$ et $(F) : x^{2} + b x + a = 0$

Soit $Δ_{1}$ le discriminant de $(E)$ et $Δ_{2}$ celui de $(F)$ , et les propositions :

$P_{1} : « Δ_{1} \geq 0 »$ et $P_{2} : « Δ_{2} \geq 0 »$

Montrer que la proposition $(P_{1} o u P_{2})$ est vraie.

3-3/ Conjonction de deux propositions

Définition

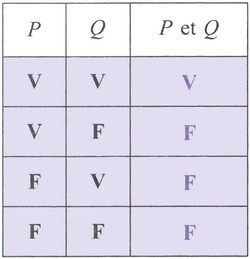
La conjonction de deux propositions $P$ et $Q$ est la proposition qu'on note $(P e t Q)$ .

Elle est vraie seulement si $P$ et $Q$ sont toutes les deux vraies.

La conjonction est un connecteur logique binaire défini par la table de vérité :

Remarques

Les propositions $(P e t Q)$ et $(Q e t P)$ ont le même sens. On dit que la conjonction est une opération commutative.

Les propositions $[(P e t Q) e t R]$ et $[P e t (Q e t R)]$ ont le même sens. On dit que la conjonction est une opération associative.

Les propositions $[P e t (Q o u R)]$ et $[(P e t Q) o u (P e t R)]$ ont le même sens. On dit que la conjonction est distributive par rapport à la disjonction.

Les propositions $[P o u (Q e t R)]$ et $[(P o u Q) e t (P o u R)]$ ont le même sens. On dit que la disjonction est distributive par rapport à la conjonction. (Pour démontrer ces résultats, il suffit d'utiliser les tables de vérité).

Applications

Soit $P$ une proposition.

Montrer que la proposition $\bar{(\bar{P} e t P)}$ est vraie.

Déterminer les réels $x$ et $y$ tels que : $(y = 3 x - 1 e t x^{2} - x = 0)$

En utilisant la distributivité de la conjonction logique par rapport à la disjonction logique, résoudre dans les système suivants :

$(S_{1}) : \{\begin{cases} x^{2} - y^{2} = 0 \\ 2 x^{2} + y^{2} = 3 \end{cases} (S_{2}) : \{\begin{cases} x y - x + y = 1 \\ 2 x^{2} - x y - y = 0 \end{cases} (S_{3}) : \{\begin{cases} 4 x^{2} - y^{2} = 0 \\ (x - 2) (y - 6) = 0 \end{cases}$

Soit $x$ et $y$ deux réels tels que $x \geq 1$ et $y \geq 1$ .

Montrer que : $\sqrt{x - 1} + \sqrt{y - 1} \leq x y$

Déterminer le domaine de définition de la fonction $f$ définie par :

$f (x) = \sqrt{x^{2} - 1} + \frac{x}{2 x - 3}$

3-4/ Implication de deux propositions

Définition

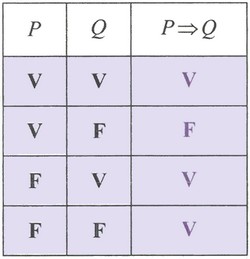
L'implication d'une proposition $P$ à une proposition $Q$ est la proposition qu'on note $(P \Rightarrow Q)$ .

Elle est fausse seulement si $P$ est vraie et $Q$ est fausse.

Les deux propositions $(P \Rightarrow Q)$ et $(\bar{P} o u Q)$ ont la même valeur de vérité.

L'implication est un connecteur logique binaire défini par la table de vérité :

Applications

Déterminer la valeur de vérité des propositions suivantes :

- $P_{1}$ : « (13 est premier) $\Rightarrow$ (56 est divisible par 13) »

- $P_{2}$ : « (47 est premier) $\Rightarrow$ (47 est impair) » .

Soit $x$ et $y$ deux réels non nuls.

On considère les deux propositions $P : « 2 x + 4 y = 1 »$ et $Q : « \frac{1}{x^{2} + y^{2}} \leq 20 »$ .

Montrer que $P \Rightarrow Q$ .

Soit $a$ et $b$ deux réels.

Montrer que : $(|a| < 1 e t |b| < 1) \Rightarrow |a + b| < |1 + a b|$

Soit $x$ un nombre réel.

Montrer les implications suivantes :

$\sqrt{x^{2} + 1} - x = 2 \Rightarrow \sqrt{x^{2} + 1} + x = \frac{1}{2} |x| + |x - 1| = x \Rightarrow x = 1$

Soit $x$ , $y$ et $z$ trois réels dont l'un est nul et les deux autres sont de signes contraires.

On suppose que les réels $x$ , $y$ et $z$ vérifient les implications suivantes :

$x = 0 \Rightarrow y = 0; x > 0 \Rightarrow y < 0; y \neq 0 \Rightarrow z > 0$

Déterminer parmi ces nombres celui qui est nul puis celui qui est strictement positif.

a- Montrer que : $(\forall a \in] 1; + \infty [) \frac{a^{2}}{a - 1} \geq 4$

b- En déduire que pour tous $a$ et $b$ de l'intervalle $] 1; + \infty [$ , on a : $\frac{a^{2}}{b - 1} + \frac{b^{2}}{a - 1} \geq 8$

Soit $(x; y) \in ℝ^{2}$ tel que $|x| \leq 1$ et $|y| \leq 1$ .

Montrer que : $\sqrt{1 - x^{2}} + \sqrt{1 - y^{2}} \leq 2 \sqrt{1 - {(\frac{x + y}{2})}^{2}}$

3-5/ Condition suffisante - condition nécessaire

Proposition

Les deux propositions suivantes sont vraies :

$[(\forall x \in E); A (x) \Rightarrow B (x)] \Rightarrow [((\forall x \in E); A (x)) \Rightarrow ((\forall x \in E); B (x))]$

$[(\exists x \in E) (\forall y \in F) A (x; y)] \Rightarrow [(\forall y \in F) (\exists x \in E) A (x; y)]$

3-6/ Équivalence de deux propositions

Définition

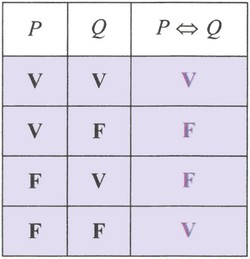
L'équivalence de deux propositions $P$ et $Q$ est la proposition qu'on note $(P \Leftrightarrow Q)$ . Elle est vraie seulement si $P$ et $Q$ ont la même valeur de vérité ; c'est-à-dire toutes les deux sont simultanément vraies ou simultanément fausses.

Les deux propositions $(P \Leftrightarrow Q)$ et $[(P \Rightarrow Q) e t (Q \Rightarrow P)]$ ont la même valeur de vérité.

L’équivalence est un connecteur logique binaire défini par la table de vérité :

Remarques

La notation $« P \Leftrightarrow Q »$ se lit « $P$ est équivalent à $Q$ » ou « $P$ équivaut à $Q$ » et correspond en français à la phrase « $P$ si et seulement si $Q$ ».

Les propositions $(P \Leftrightarrow Q)$ et $(Q \Leftrightarrow P)$ ont la même table de vérité. On dit que l'équivalence est une opération commutative.

On s'intéresse plus souvent aux équivalences vraies qu'aux fausses. En pratique, on écrira $« P \Leftrightarrow Q »$ uniquement lorsqu'il s'agit d'une assertion vraie. Autrement dit, si l'on écrit $« P \Leftrightarrow Q »$ cela sous entend « $P \Leftrightarrow Q$ est vraie».

Les expressions « condition nécessaire et suffisante », « si et seulement si », « il faut et il suffit » signifient toutes « équivalent » ou encore $« \Leftrightarrow »$ .

En pratique, dans une rédaction, on n'emploiera jamais les symboles $\Leftrightarrow$ et $\Rightarrow$ . Le seul endroit où le symbole $\Leftrightarrow$ est toléré, c'est dans les résolutions d'équations ou d'inéquations.

On préférera l'emploi de mots de français : conjonctions de coordination (mais, ou, et, donc, or, car), conjonctions de subordination (parce que, si, puisque, ...) ou adverbes (ainsi, cependant, ...).

Proposition

Soit $P$ , $Q$ et $R$ trois propositions. Alors :

$[(P \Leftrightarrow Q) e t (Q \Leftrightarrow R)] \Rightarrow (P \Leftrightarrow R)$

On dit que l’équivalence est une relation transitive.

Généralisation

Soit $P$ , $R_{1}$ , $R_{2}$ ,..., $R_{n}$ et $Q$ des propositions. Alors :

$[(P \Leftrightarrow R_{1}) e t (R_{1} \Leftrightarrow R_{2}) e t . . . e t (R_{n} \Leftrightarrow Q)] \Rightarrow (P \Leftrightarrow Q)$

Pratiquement : pour montrer qu’une proposition $P$ est vraie, on montre que les équivalences successives $P \Leftrightarrow R_{1}$ et $R_{1} \Leftrightarrow R_{2}$ et ... et $R_{n} \Leftrightarrow Q$ sont vraies et que la proposition $Q$ est vraie. Par conséquent, la proposition $P$ . Ce type de raisonnement s'appelle « raisonnement par équivalences successives » .

Applicatios

Soient $a$ et $b$ deux réels positifs.

Montrer que : $\frac{a}{\sqrt{a^{2} + 1}} < \frac{b}{\sqrt{b^{2} + 1}} \Leftrightarrow a < b$

Montrer que : $a \sqrt{1 + a^{2}} = b \sqrt{1 + b^{2}} \Leftrightarrow a = b$

Soit $(x; y) \in ℝ^{2}$ tel que $x \geq 1$ et $y \geq 4$ .

Montrer que : $\sqrt{x - 1} + 2 \sqrt{y - 4} = \frac{x + y}{2} \Leftrightarrow (x = 2 e t y = 8)$

Soit $(x; y) \in ℝ^{2}$ .

Établir les équivalences suivantes :

$|x + y| \leq \sqrt{x^{2} + 1} + \sqrt{y^{2} + 1} \Leftrightarrow |\sqrt{x^{2} + 1} - \sqrt{y^{2} + 1}| \leq |x - y|$

$(x + y) {(x - y)}^{2} < 0 \Leftrightarrow {(x + y)}^{3} > 4 (x^{3} + y^{3})$

Soit $x$ , $y$ et $z$ trois réels strictement positifs.

Établir les équivalences suivantes :

$x y \sqrt{z} < x z \sqrt{y} < y z \sqrt{x} \Leftrightarrow x < y < z$

$|x - y| < z < x + y \Leftrightarrow |\frac{x^{2} + y^{2} - z^{2}}{x y}| < 2$

Proposition

Les deux propositions suivantes sont vraies :

$[(\forall x \in E) A (x) e t B (x)] \Leftrightarrow [((\forall x \in E) A (x)) e t ((\forall x \in E) B (x))] [(\exists x \in E) A (x) o u B (x)] \Leftrightarrow [((\exists x \in E) A (x)) o u ((\exists x \in E) B (x))]$

Remarques

La proposition $[(\exists x \in E) A (x) e t B (x)] \Leftrightarrow [((\exists x \in E) A (x)) e t ((\exists x \in E) B (x))]$ n'est pas toujours vraie comme le montre l'exemple suivant :

Considérons les deux propositions suivantes :

$P : « ((\exists x \in ℝ) \cos x = 0) e t ((\exists x \in ℝ) \sin x = 0) » Q : « ((\exists x \in ℝ) \cos x = 0 e t \sin x = 0) »$

La proposition $P$ est vraie car $0$ est un réel $x$ tel que $\sin x = 0$ et $\frac{π}{2}$ est un réel $x$ tel que $\cos x = 0$ .

Ainsi, dans les deux affirmations $((\exists x \in ℝ) \cos x = 0) e t ((\exists x \in ℝ) \sin x = 0)$ , la lettre $x$ utilisée deux fois ne désigne pas forcément un même nombre. La proposition $Q$ est évidement fausse car pour tout $x \in ℝ : \cos^{2} x + \sin^{2} x = 1 \neq 0$

En pratique, pour montrer que $P \Leftrightarrow Q$ , on peut utiliser un des raisonnements suivants :

Raisonnement par double implication :

Pour ce type de raisonnement, on suppose que la proposition $P$ est vraie et on montre que $Q$ est vraie et réciproquement.

La démonstration se fait donc en deux étapes: une première débutant par « Supposons $P$ et montrons $Q$ » et une seconde débutant par « Supposons $Q$ et montrons $P$ ».

On passe ensuite de $P$ à $Q$ et de $Q$ à $P$ en utilisant à chaque fois des implications.

Raisonnement par équivalences successives :

Pour ce type de raisonnement, on procède en une seule étape. On passe alors de $P$ à $Q$ (ou bien de $Q$ à $P$ ) en utilisant à chaque fois des équivalences.

Cette méthode est plus courte que la précédente (une seule étape au lieu de deux) mais peut être plus fastidieuse puisqu'on doit vérifier que chaque enchaînement logique de la démonstration est bien une équivalence et pas seulement une implication.

Le raisonnement par équivalences successives est généralement réservé à la résolution d'équations et d'inéquations. On lui préférera en général le raisonnement par double implication.

Retour