Math 3AC - Semestre 2 Devoir 3 Modèle 2

Exercice 1 (6 pts)

$f$ est une fonction linéaire telle que $f\left(x\right)=\frac{-1}{4}x$.

1. Calculer $f\left(4\right)$.

2. Construire $\left(D\right)$ la représentation graphique de $f$ dans un repère orthonormé $\left(O,I,J\right)$.

$g$ est une fonction affine de coefficient $3$ et $g\left(2\right)=4$.

3. Montrer que : $g\left(x\right)=3x-2$

4. Calculer l'image de $1$ par la fonction $g$.

5. Déterminer le nombre réel $x$ dont l'image est $-1$ par la fonction $g$.

6. Construire $\left(\Delta \right)$ la représentation graphique de $g$ dans le même repère $\left(O,I,J\right)$.

7. Calculer les coordonnées du point $K$ l'intersection de $\left(D\right)$ et $\left(\Delta \right)$.

Exercice 2 (5 pts)

On considère la fonction affine $f$ telle que $f\left(x\right)=3x-2$,  et $\left(\Delta \right)$ sa représentation graphique.

1. Calculer $f\left(1\right)$ et $f\left(\frac{1}{3}\right)$.

2. Montrer que $B\left(\frac{3}{2};\frac{5}{2}\right)$ appartient à $\left(\Delta \right)$.

3. Représenter $\left(\Delta \right)$.

$g$ est une fonction linéaire et $\left(L\right)$ sa représentation graphique telle que $\left(L\right)$ coupe $\left(\Delta \right)$ en $B$.

4. Représenter $\left(L\right)$ dans le repère $\left(O,I,J\right)$.

5. Définir $g\left(x\right)$.

Exercice 3 (4 pts)

La série statistique suivante représente la cotisation des élèves de 3AC à une compagne de solidarité :

1. Compléter le tableau statistique.

2. Déterminer le mode et la médiane de cette série statistique.

3. Vérifier que la moyenne arithmétique est 43dhs.

4. Calculer le pourcentage des élèves qui ont cotisé d'un montant strictement supérieur à 40dhs.

Exercice 4 (5 pts)

$SABCD$ est une pyramide de base le carré $ABCD$ et sa hauteur $\left[SA\right]$.

On pose : $AB=3cm$ et $SB=5cm$

1. Montrer que $SA=4cm$.

2. Calculer le volume de la pyramide $SABCD$.

$I$ un point de $\left[SA\right]$ tel que $SI=2,4cm$.

Le plan passant par $I$ et parallèle à $\left(ABCD\right)$ coupe $\left[SB\right]$ en $J$, $\left[SC\right]$ en $K$ et $\left[SD\right]$ en $L$ :

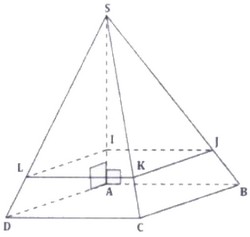
3. Calculer le rapport de réduction.

4. Montrer que $IJ=1,8cm$.

5. Calculer le volume de la pyramide $SIJKL$.