
Physique et Chimie : 2ème Année Bac SVT-STE-STM
Semestre 2 Devoir 2 Modèle 1
Professeur : Mr El GOUFIFA Jihad
Exercice 1 (7 pts)
L’odeur caractéristique de la plupart des fruits est due à l’ester qu’ils contiennent. L’ester contenu dans l’ananas par exemple est le butanoate d’éthyle dont la formule semi-développée est la suivante :
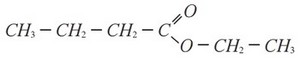
Pour subvenir aux besoins de l’industrie agroalimentaire, on synthétise cet ester facilement et à coût moins élevé.
Données :
On obtient le butanoate d’éthyle en faisant réagir un acide carboxylique avec un alcool , en présence d’acide sulfurique, selon l’équation suivante :

- Citer les caractéristiques de cette réaction.
- Indiquer la formule semi-développée de chacun des réactifs et et les nommer.
On chauffe par reflux un mélange équimolaire contenant de l’acide et de l’alcool en présence d’acide sulfurique.
À l’équilibre chimique, on obtient de butanoate d’éthyle.
- Dresser le tableau d’avancement de l’équation précédente.
- Calculer la valeur de la constante d’équilibre associée à l’équation de la réaction étudiée.
- Calculer la valeur du rendement de cette réaction.
On refait la même réaction en utilisant de l’acide et de l’alcool .
- Comment peut-on augmenter le rendement de cette réaction ?
- Quelle doit être la valeur de pour obtenir un rendement ?
Exercice 2 (7 pts)
On considère un skieur de masse , assimilé à un point matériel, se déplace sur une piste horizontale sous l’action d’une force , d’intensité exercée par une corde horizontale :
Les frottements sont équivalents à une force considérée constante et de sens opposé au mouvement et d’intensité .
Pour étudier ce mouvement, on choisit un repère lié à la terre, et on considère l’instant de départ du skieur en comme origine des dates.
- Déterminer l’équation différentielle vérifiée par la vitesse .
La figure suivante représente les variations de la vitesse en fonction du temps :
- Quelle est la nature du mouvement de ? Justifier.
- Déterminer l’équation de la vitesse , et déduire la valeur de l’accélération .
- Calculer l’intensité de la force des frottements.
Le skieur passe par la position à l’instant .
- Déterminer la distance .
- Déterminer la vitesse à la position .
Données :
Exercice 3 (6 pts)
Un pendule élastique est constitué d'un mobile de masse pouvant se déplacer sur un banc à coussin d'air horizontal. Ce mobile est attaché à un point fixe par un ressort de masse négligeable à spires non jointives, de raideur .
La position du mobile est repérée par l'abscisse x sur l'axe .
A l'équilibre, la position du centre d'inertie coïncide avec le point , origine des abscisses.
On considère que le mobile n'est soumis à aucune force de frottement.
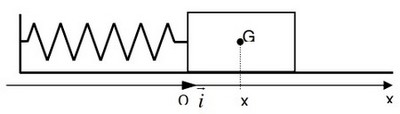
- Indiquer l'expression vectorielle de la force de rappel du ressort en fonction de l'abscisse du centre d'inertie du mobile et de vecteur unitaire.
- Faire l'inventaire des forces qui s'exercent sur le mobile, puis reproduire le schéma ci-dessus et représenter ces forces.
- À l'aide de la deuxième loi de Newton, établir l'équation différentielle du mouvement.
- Sachant que la solution de l’équation différentielle du mouvement est de la forme , déterminer l’expression de la période propre .
Un dispositif d'enregistrement de la position du mobile permet de mesurer la valeur de la période du mouvement :
- Quelle est la valeur numérique de la raideur .
- Montrer que l’énergie mécanique du système est constante et calculer sa valeur pour .


