PC 2Bac SVT-STE-STM - Semestre 2 Devoir 1 Modèle 1

Physique et Chimie : 2ème Année Bac SVT-STE-STM

Semestre 2 Devoir 1 Modèle 1

Professeur : Mr El GOUFIFA Jihad

Exercice 1 (6 pts)

On considère la pile suivante :

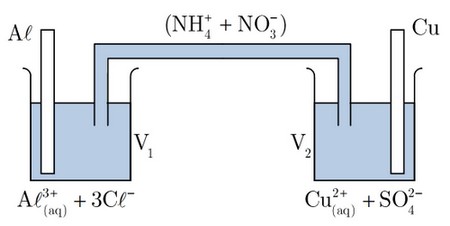
Données :

Les volumes des solutions dans les deux demi-piles valent : $V_{1} = V_{2} = 50 m L$
La concentration effective initiale : ${[C u_{(a q)}^{2 +}]}_{i} = 0, 10 m o l . L^{- 1}$

Lorsqu’on branche un voltmètre électronique avec sa borne COM reliée à l’électrode d’aluminium, on mesure une différence de potentiel $U = + 1, 6 V$ .

On donne : $F = 96500 C . m o l^{- 1}$ et $M (A l) = 27 g . m o l^{- 1}$

Quelle est la polarité de la pile ?

On relie la pile à un petit moteur électrique.

Faire un schéma du dispositif. Indiquer le sens du courant dans le circuit.

Préciser la nature et le sens des porteurs de charges dans ce circuit.

Donner les équations des réactions (qui se produisent aux électrodes. Préciser où ont lieu l’oxydation et la réduction. Identifier l’anode et la cathode.

Écrire l’équation de l’oxydoréduction spontanée qui se produit dans la pile.

La pile fonctionne pendant 1,0 heure en débitant un courant d’intensité $50 m A$ .

Calculer la variation $Δ m (A l)$ de la masse d’aluminium métallique.

Calculer la variation de concentration $Δ [C u^{2 +}]$ en ions cuivre II $C u^{2 +}$ .

Exercice 2 (5 pts)

On se propose de déterminer le coefficient d’inductance $L$ et de la résistance $r$ d’une bobine $(b)$ .

Pour cela on réalise le montage qui se compose de :

Bobine $(b)$ .
Résistor de résistance $R = 90 Ω$ .
Générateur de force électromotrice $E$ et de résistance négligeable.
Interrupteur $K$ .

On ferme l’interrupteur à un instant de date $t = 0$ .

Un système d’acquisition informatisé permet de tracer les courbes $(C_{1})$ et $(C_{2})$ représentant successivement l’évolution de l’intensité du courant $i (t)$ traversant le circuit et l’évolution de la tension $u_{L} (t)$ aux bornes de la bobine.

La droite $(T)$ représente la tangente à la courbe $(C_{1})$ à $t = 0$ :

Établir l’équation différentielle régissant l’établissement du courant $i (t)$ dans le circuit.

Trouver les expressions de $A$ et de $τ$ en fonction des paramètres du circuit pour que l’expression $i (t) = A . (1 - e^{- \frac{t}{τ}})$ soit solution de cette équation différentielle.

Déterminer l’expression de la tension $u_{R} (t)$ aux bornes du conducteur ohmique.

En exploitant les deux courbes $(C_{1})$ et $(C_{2})$ , lorsque le régime permanent est atteint, déterminer la valeur de $r$ , et la valeur de la constante du temps $τ$ .

Vérifier que $L = 1 H$ .

Calculer l’énergie $E_{m}$ emmagasinée par la bobine en régime permanent.

Déterminer l’instant $t$ auquel la bobine a stocké $75 %$ de son énergie maximale.

Exercice 3 (9 pts)

Le but de cet exercice est de déterminer les deux caractéristiques d'une bobine d'un haut-parleur, en réalisant deux expériences différentes.

Expérience 1

Un haut-parleur contient une bobine de coefficient d'inductance $L$ et de résistance interne $r$ .

Pour déterminer ces deux grandeurs, on a réalisé le montage électrique suivant où $E = 12 V$ et $R = 42 Ω$ .

Juste après la fermeture du circuit, on visualise à l'aide d'un dispositif informatique convenable, l'évolution de la tension $u_{R}$ en fonction du temps :

Montrer que la tension $u_{R}$ aux bornes du résistor vérifie l'équation différentielle $τ \frac{d u_{R}}{d t} + u_{R} = A$ , en exprimant les constantes $A$ et $τ$ en fonctions des paramètres du circuit.

S'assurer que la constante $τ$ est homogène à un temps.

Trouver la valeur de la résistance $τ$ .

Trouver la valeur du coefficient d'inductance $L$ de la bobine.

Expérience 2

On monte la bobine précédente, en série, avec un condensateur (initialement chargé complètement) de capacité $C = 0, 2 µ F$ et un résistor de résistance $R' = 200 Ω$ .

On obtient, à l'aide du même dispositif informatique, la courbe suivante qui représente les variations de la tension $u_{C}$ aux bornes du condensateur en fonction du temps :

À quel des trois régimes d'oscillations, correspond la courbe ci-dessus ?

Établir l'équation différentielle vérifiée par la tension $u_{C}$ .

En considérant que la pseudo-période $T$ est égale la période propre $T_{0}$ de l'oscillateur $L C$ , vérifier la valeur de l'inductance de la bobine étudiée.

Calculer l'énergie dissipée par effet joule entre les instants $t_{0} = 0$ et $t_{1} = \frac{3}{2} T$ .

Pour compenser l'énergie dissipée, on monte en sérié dans le circuit précédent un générateur maintenant entre ses bornes une tension uG proportionnelle à l'intensité du courant, tel que $u_{G} (t) = k . i (t)$ .

Établir, dans ce cas, l'équation différentielle vérifiée par la charge $q (t)$ du condensateur.

On fixe le paramètre $k$ sur la valeur $208, 4$ pour obtenir des oscillations électriques sinusoïdales.

Vérifier la valeur de la résistance $r$ de la bobine étudiée.

Retour