Math 2Bac SPC - Semestre 1 Devoir 3 Modèle 2

I- Exercice 1

Soit $g$ la fonction numérique définie sur l’intervalle $]0,+\infty [$ par : $g\left(x\right)=x^2+x-2+2\ln x$

1. Vérifier que $g\left(1\right)=0$.

2. À partir du tableau de variations de la fonction $g$, montrer que $g\left(x\right)\le 0$ pour tout $x$ appartenant à l’intervalle $]0;1]$, et que $g\left(x\right)\ge 0$ pour tout $x$ appartenant à l’intervalle $[1;+\infty [$.

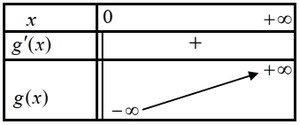
On considère la fonction numérique $f$ définie sur l’intervalle $]0,+\infty [$ par : $f\left(x\right)=x+\left(1-\frac{2}{x}\right)\ln x$

Soit $\left({\mathcal{C}}_f\right)$ la courbe représentative de la fonction $f$ dans un repère orthonormé $\left(O,\overrightarrow{i},\overrightarrow{j}\right)$ (unité : 1cm).

3. Montrer que $\underset{x\to 0^{+}}{\lim }f\left(x\right)=+\infty$, et interpréter géométriquement le résultat.

4. Montrer que $\underset{x\to +\infty }{\lim }f\left(x\right)=+\infty$.

5. Montrer que la courbe $\left({\mathcal{C}}_f\right)$ admet au voisinage de $+\infty$ une branche parabolique de direction asymptotique celle de la droite $\left(D\right)$ d’équation $y=x$.

6. Montrer que $f\text{'}\left(x\right)=\frac{g\left(x\right)}{x^2}$ pour tout $x$ appartenant à l’intervalle $]0,+\infty [$.

7. Montrer que $f$ est décroissante sur l’intervalle $]0;1]$, et croissante sur l’intervalle $[1;+\infty [$.

8. Dresser le tableau de variations de la fonction $f$ sur l’intervalle $]0,+\infty [$.

9. Résoudre dans l’intervalle $]0,+\infty [$ l’équation $\left(1-\frac{2}{x}\right)\ln x=0$.

10. En déduire que la courbe $\left({\mathcal{C}}_f\right)$ coupe la droite $\left(D\right)$ en deux points dont on déterminera les coordonnées.

11. Montrer que $f\left(x\right)\le x$ pour tout $x$ appartenant à l’intervalle $\left[1;2\right]$, et en déduire la position relative de la courbe $\left({\mathcal{C}}_f\right)$ et la droite $\left(D\right)$ sur l’intervalle $\left[1;2\right]$.

12. Construire, dans le même repère $\left(O,\overrightarrow{i},\overrightarrow{j}\right)$, la droite $\left(D\right)$ et la courbe $\left({\mathcal{C}}_f\right)$ (On admettra que la courbe $\left({\mathcal{C}}_f\right)$ possède un seul point d’inflexion dont l’abscisse est comprise entre $2,4$ et $2,5$).

II- Exercice 2

Le plan complexe est rapporté à un repère orthonormé direct $\left(O,\overrightarrow{u},\overrightarrow{v}\right)$.

On considère les points $A$, $B$ et $C$ d'affixes respectives $a=2$ , $b=\sqrt{2}\left(-1+i\right)$ et $c=\sqrt{2}\left(-1-i\right)$.

Soit $E$ d’affixe $e$ le milieu de segment $\left[AB\right]$.

1. Donner une forme trigonométrique des nombres complexes $a$, $b$ et $c$.

2. Placer les points $A$, $B$ et $C$ sur le repère $\left(O,\overrightarrow{u},\overrightarrow{v}\right)$.

3. Montrer que le triangle $OAB$ est isocèle, puis déduire un mesure de l'angle orienté $\left(\overline{\overrightarrow{u},\overrightarrow{OE}}\right)$.

4. Déterminer $e$, puis $\left|e\right|$.

5. Déduire $\cos \left(\frac{3\mathrm{\pi }}{8}\right)$ et $\sin \left(\frac{3\mathrm{\pi }}{8}\right)$.