
Mathématiques : Tronc Commun
Séance 15 (Statistiques)
Professeur : Mr ETTOUHAMY Abdelhak
Sommaire
I- Terminologie statistique et symboles
1-1/ Population – Unité statistique – Caractère – Valeurs – Classes
1-2/ Effectifs – Effectifs cumulés – Fréquences – Fréquences cumulées – Pourcentages
II- Paramètres de position
2-1/ Moyenne arithmétique (ou moyenne statistique)
2-2/ Médiane
III- Paramètres de dispersion
3-1/ Étendue
3-2/ Écart moyen
3-3/ Variance
3-4/ Écart type
IV- Diagrammes
4-1/ Diagramme en bâtons et polygone statistique
4-2/ Diagramme sectoriel
4-3/ Histogramme
V- Exercices
5-1/ Exercice 1
5-2/ Exercice 2
5-3/ Exercice 3
5-4/ Exercice 4
I- Terminologie statistique et symboles
1-1/ Population – Unité statistique – Caractère – Valeurs – Classes
Activité
- Exemple 1
Dix candidats ont passé un concours , les notes obtenues sur 150 points sont :
60 – 70 – 80 – 60 – 60 – 70 – 90 – 70 – 60 – 80
- Exemple 2
Le tableau suivant présente les poids de 60 bébés âgés de 4 mois :
| Poids des bébés en kg | [5;5,5[ | [5,5;6[ | [6;6,5[ | [6,5;7[ | [7;7,5[ |
| Nombres de bébés | 200 | 50 | 30 | 15 | 5 |
- Exemple 3
Le tableau suivant donne le nombre des voitures vendues de chaque marque parmi 300 voitures vendues pendant un mois :
| Marques des voitures | Dacia | Peugeot | Ford | Mercedes | BMW |
| Nombres des voitures vendues | 200 | 50 | 30 | 15 | 5 |
Terminologie statistique
| Termes | Exemple 1 | Exemple 2 | Exemple 3 |
| Population statistique | 10 candidats | 60 bébés | 300 voitures vendues |
| Effectif total (noté N) | N=10 | N=60 | N=300 |
| Unité statistique ou « individu» | Candidat | Bébé | Voiture vendue |
| Caractère (ou variable statistique) | Note obtenue | Poids du bébé | Marque de la voiture |
| Types de caractères | Caractère quantitatif discret | Caractère quantitatif continue | Caractère qualitatif |
| : valeurs du caractère : classes du caractère |
Suivant le sens croissant : |
La 1ère classe est La dernière classe est Le représentant est le milieu de l’intervalle |
I- Terminologie statistique et symboles
1-1/ Population – Unité statistique – Caractère – Valeurs – Classes
Remarques
Le caractère quantitatif discret prend des valeurs isolées (comme les mois de naissances des élèves ou le nombre des membres de la famille pour chaque élève d’une classe de tronc commun .
Le caractère quantitatif continue prend des valeurs très proches (comme les poids ou les hauteurs des
élèves d’un lycée), dans ce cas les valeurs du caractères sont rassemblées dans des intervalles demi
ouverts de même longueur ou de même capacité, chaque intervalle est appelé classe.
Le caractère qualitatif ne peut pas s’exprimer par des nombres (comme les couleurs des yeux ou les marques des voitures préférées).
I- Terminologie statistique et symboles
1-2/ Effectifs – Effectifs cumulés – Fréquences – Fréquences cumulées – Pourcentages
Effectifs
Le nombre de fois tel qu’une valeur est répétée s’appelle effectif, on la note .
La somme des effectifs est le nombre total de la population statistique.
Le couple s’appelle une série statistique.
Toute valeur ou toute classe ayant le plus grand effectif s’appelle valeur (ou classe) modale.
On peut avoir plusieurs valeurs modes (valeurs modales) ou classes modes (ou classes modales).
I- Terminologie statistique et symboles
1-2/ Effectifs – Effectifs cumulés – Fréquences – Fréquences cumulées – Pourcentages
Effectifs cumulés
est une série statistique.
Le nombre s’appelle l’effectif cumulé de la valeur d’un caractère.
I- Terminologie statistique et symboles
1-2/ Effectifs – Effectifs cumulés – Fréquences – Fréquences cumulées – Pourcentages
Fréquences
est une série statistique.
Le nombre s’appelle la fréquence de la valeur d’un caractère.
On note :
I- Terminologie statistique et symboles
1-2/ Effectifs – Effectifs cumulés – Fréquences – Fréquences cumulées – Pourcentages
Fréquences cumulées
est une série statistique.
Le nombre s’appelle la fréquence cumulée de la valeur d’un caractère.
I- Terminologie statistique et symboles
1-2/ Effectifs – Effectifs cumulés – Fréquences – Fréquences cumulées – Pourcentages
Pourcentages
est une série statistique.
Le nombre s’appelle le pourcentage de la valeur d’une caractère .
On note :
La somme des pourcentage est égale à .
II- Paramètres de position
2-1/ Moyenne arithmétique (ou moyenne statistique)
Définition
La moyenne arithmétique d’une série statistique est le nombre tel que :
avec est le nombre des valeurs et .
Remarque
Dans le cas d’une série statistique où les valeurs sont exprimées par classes , les valeurs sont remplacés par les milieux des classes .
Donc :
avec est le nombre de classes.
Exemple
II- Paramètres de position
2-2/ Médiane
Définition
La plus petite valeur du caractère dont l’effectif cumulé est plus grand ou égal à la moitié de l’effectif total est appelée la médiane.
On la note .
Exemple
III- Paramètres de dispersion
3-1/ Étendue
Définition
La différence entre deux valeurs extrêmes s’appelle l’étendue.
Exemple
III- Paramètres de dispersion
3-2/ Écart moyen
Définition
La moyenne des écarts à la moyenne statistique s’appelle l’écart-moyen, on la note :
Exemple
III- Paramètres de dispersion
3-3/ Variance
Définition
La variance d’une série statistique est le nombre tel que :
avec est le nombre des valeurs , et , et est la moyenne arithmétique de la série statistique.
Propriété
La variance d’une série statistique est :
La variance est toujours positive.
Exemple
III- Paramètres de dispersion
3-4/ Écart type
Définition
L’écart type d’une série statistique est le nombre tel que , avec est la variance de la série statistique.
Exemple
IV- Diagrammes
4-1/ Diagramme en bâtons et polygone statistique
Exemple
| Valeurs | |||||
| Effectifs | |||||
| Fréquences |
Diagramme en bâtons des effectifs
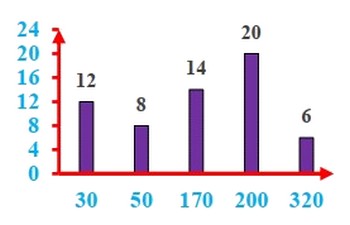
Polygone statistique des effectifs
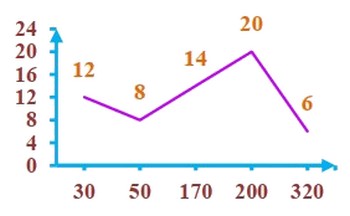
Diagramme en bâtons des fréquences
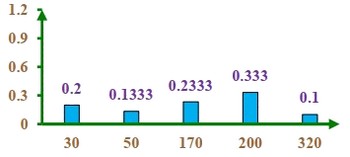
Polygone statistique des fréquences

IV- Diagrammes
4-2/ Diagramme sectoriel
Exemple
| Valeurs | |||||
| Effectifs | |||||
Diagramme sectoriel sur un cercle tout entier
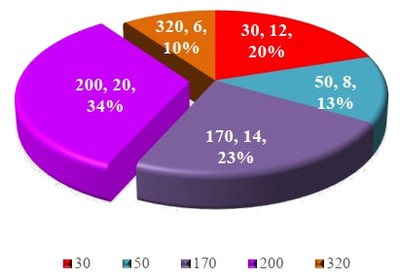
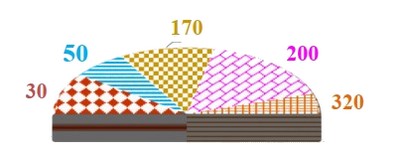
Diagramme sectoriel sur un demi cercle
IV- Diagrammes
4-3/ Histogramme
Exemple
| Classe | |||||
| Effectifs | 2 | 7 | 3 | 10 | 8 |
Histogramme des effectifs des classes d'amplitude 10

V- Exercices
5-1/ Exercice 1
Un ensemble de famille est décrit d’après le nombre des enfants :

- Faire une représentation graphique des effectifs.
- Représenter le polygone des effectifs.
- Donner la moyenne.
- Calculer la médiane
V- Exercices
5-2/ Exercice 2
Voici le relevé d’une étude statistique sur les tailles en cm de 300 élèves d’un établissement :

- Faire le calcul des fréquences, mode, médiane, moyenne, variance.
- Faire la représentation graphique des effectifs, ainsi que le polygone des effectifs.
V- Exercices
5-3/ Exercice 3
La vitesse d’un certain nombre de voiture a été contrôlé sur une autoroute, et on a obtenu le tableau suivant :

- Faire le calcul des fréquences, mode, , moyenne,
- Faire la représentation graphique des effectifs.
V- Exercices
5-4/ Exercice 4
Le tableau suivant récapitule les moyennes annuelles en Mathématiques d’élèves de seconde :

- Compléter la distribution des fréquences.
- Que signifie ECC ? compléter la ligne correspondante.
- Utiliser le tableau pour déterminer la médiane, les premier et troisième quartiles.
- Tracer le polygone des effectifs.


