
Mathématiques : 2Bac SMA-SMB
Séance 12-1-1 : Calcul de probabilités - Partie 1 (Cours)
Professeur : Mr CHEDDADI Haitam
Sommaire
I- Le jargon des probabilités
1-1/ Expérience aléatoire - notion d’événement
1-2/ Opérations sur les événements
1-3/ Systèmes complets d'événements
II- Probabilité d’un événement
2-1/ Loi de probabilité sur un ensemble fini
2-2/ Hypothèse d'équiprobabilité
III- Probabilité conditionnelle
3-1/ Introduction
3-2/ Formule des probabilités composées
3-3/ Formule des probabilités totales
I- Le jargon des probabilités
1-1/ Expérience aléatoire - notion d’événement
Définition 1
Une expérience aléatoire (ou épreuve aléatoire) est une mise en œuvre, dans des conditions bien définies, d'un processus évolutif pour un système (matériel ou modèle) dont l'état final est observable (expérience concrète) ou imaginable (expérience abstraite) mais imprévisible. Un tel état final est appelé résultat de l'expérience aléatoire.
L'ensemble des résultats possibles d'une expérience aléatoire est appelé univers (ou univers des possibilités, ou ensemble fondamental), noté en général .
Un élément de cet ensemble est appelé une issue ou une éventualité. Il est dit réalisé s'il est effectivement constaté lors d'un déroulement particulier de l'expérience aléatoire.
I- Le jargon des probabilités
1-1/ Expérience aléatoire - notion d’événement
Définition 2
On appelle événement lié à une expérience aléatoire, tout résultat de cette expérience pouvant se produire.
Chaque événement lié à cette expérience aléatoire est une partie de l'univers de ses résultats observables.
I- Le jargon des probabilités
1-1/ Expérience aléatoire - notion d’événement
Remarques
La définition 2 montre qu'un événement est une propriété attachée à l'expérience aléatoire qui peut être vérifiée ou non.
Il est bon de remarquer qu'un événement se réalise lorsque le résultat constaté de l'épreuve est l'un des éléments qui constituent l'événement.
L'ensemble de tous les événements est égal à l'ensemble de toutes les parties de , qu'on note .
I- Le jargon des probabilités
1-1/ Expérience aléatoire - notion d’événement
Définition 3
Soit l'univers lié à une expérience aléatoire.
- L'événement se réalise toujours, et est appelé l'événement certain.
- L'événement ne se réalise jamais, et appelé l'événement impossible.
- L'événement , où est appelé événement élémentaire.
I- Le jargon des probabilités
1-2/ Opérations sur les événements
Définition 4
Soit l'univers lié à une expérience aléatoire. et étant deux événements de .
1- L’événement « et » est réalisé si, et seulement si, et sont réalisés au cours de la même expérience. Cet événement est appelé l'intersection des événements et , et on le note .
2- L'événement « ou B » est réalisé si, et seulement si, l’un au moins des deux événements ou est réalisé au cours de la même expérience. Cet événement est appelé la réunion des événements et , et on le note .
3- L’événement « non » est réalisé si, et seulement si, n’est pas réalisé. Cet événement est appelé l’événement contraire de , et on le note .
4- On dit que les événements et sont incompatibles ou disjoints s’ils ne peuvent pas être réalisés simultanément. Donc, et sont incompatibles si, et seulement si, .
I- Le jargon des probabilités
1-2/ Opérations sur les événements
Diagramme de Venn
Pour bien comprendre les opérations sur les événements et ses propriétés, on utilise une création mathématique intéressant qui s'appelle diagramme de Venn.
Ce diagramme permet de représenter sur une figure, un ensemble et certaines de ses parties.
A titre d’exemple :

I- Le jargon des probabilités
1-2/ Opérations sur les événements
Tableau récapitulatif
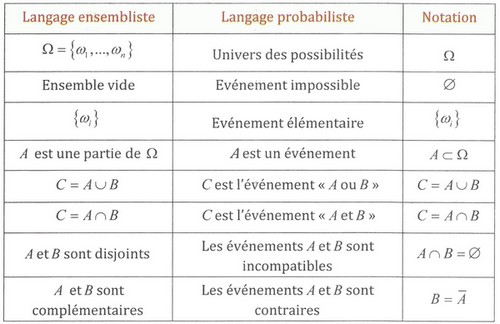
I- Le jargon des probabilités
1-2/ Opérations sur les événements
Proposition 1
Soit l’univers lié à une expérience aléatoire.
, et des événements de .
On a alors les propriétés suivantes :
Remarques
Comme dans le langage ensembliste, les égalités et portent le nom de « les lois de Morgan ».
L’égalité joue un rôle important en calcul des probabilités.
I- Le jargon des probabilités
1-3/ Systèmes complets d'événements
Définition 5
Soit l’univers lié à une expérience aléatoire et des événements de .
On dit que forment un système complet d’événements lorsque les deux conditions suivantes sont vérifiées :
- Les événements sont deux à deux incompatibles :
- Les événements sont complémentaires :
Exemple
forme un système complet d’événements de :

I- Le jargon des probabilités
1-3/ Systèmes complets d'événements
Remarques
1- Pour tout événement non vide de , les événements et forment un système complet d’événements car et .
2- Pour tout univers fini , les événements élémentaires forment un système complet d’événements.
II- Probabilité d’un événement
2-1/ Loi de probabilité sur un ensemble fini
Définition 6
Soit un ensemble fini.
- Définir une loi de probabilité sur , c'est attribuer à chaque éventualité un réel de telle sorte que .
On dit alors que la probabilité de l'événement élémentaire est , et on écrit :
- Étant donné un événements , on définit alors la probabilité de , et on note comme la somme des probabilités des événements élémentaires qui constituent .
Le couple est appelé un espace probabilisé fini.
II- Probabilité d’un événement
2-1/ Loi de probabilité sur un ensemble fini
Proposition 2
Soit l’univers lié à une expérience aléatoire, et une probabilité définie sur .
Soit et deux événements de .
On a alors les propriétés suivantes :
1-
2- Si et sont incompatibles alors :
3- et
En particulier, si alors : et
4-
II- Probabilité d’un événement
2-2/ Hypothèse d'équiprobabilité
Définition 7
Soit l'univers lié à une expérience aléatoire, et une probabilité définie sur .
On dit qu'il y a équiprobabilité, lorsque les probabilités de tous les événements élémentaires sont égales.
On dit aussi que est la probabilité uniforme sur .
II- Probabilité d’un événement
2-2/ Hypothèse d'équiprobabilité
Proposition 3
Dans le cas d’équiprobabilité, on a les formules suivantes :
1) Pour tout :
2) Pour tout événement de :
II- Probabilité d’un événement
2-2/ Hypothèse d'équiprobabilité
Remarques
1- Si l’énoncé du problème contient des phrases comme : « dé non pipé », « pièce non truquée », « manière équiprobable », « tirage au hasard », « boules indiscernables au toucher », ...etc., cela signifie qu’il s’agit bien d’une équiprobabilité. Bien entendu, dans la limite des programmes, on s’intéresse de façon générale à l’équiprobabilité dans la résolution des problèmes.
Mais si l’énoncé indique qu’il n’y a pas d’équiprobabilité, on aura besoin d'autres informations pour résoudre le problème.
2- Jusqu'à présent, pour calculer la probabilité d'un événement , on peut envisager les stratégies suivantes :
- Exprimer en fonction d’événements de probabilités connues dans le langage des événements ;
- Modéliser par une expression ensembliste. Cette traduction se fait en remplaçant les « et » par des « n », les « ou » par des « u » et les négations par des complémentaires ;
- Simplifier ou transformer l'expression obtenue grâce au calcul ensembliste de façon à pouvoir appliquer les formules des calculs des probabilités ; on pourra utiliser dans les simplifications les diagrammes ensemblistes.
III- Probabilité conditionnelle
3-1/ Introduction
Définition 8
Soit une probabilité définie sur un univers , et soit un événement tel que .
Pour tout événement , on pose :
est une probabilité définie sur , appelée probabilité conditionnelle relative à ou probabilité conditionnel sachant .
s'appelle « la probabilité de sachant que est réalisé » ou « la probabilité de sachant » ou encore « la probabilité de conditionnellement à ».
III- Probabilité conditionnelle
3-1/ Introduction
Remarques
- La probabilité de sachant est à bien distinguer de la probabilité de l’intersection de et de égale à . En effet dans le calcul de la probabilité , nous supposons implicitement que l’événement est réalisé tandis que dans le calcul de la probabilité , nous cherchons la probabilité de l’événement ( et ) où l’événement n’est pas a priori réalisé.
- Au lieu de , on note aussi . Cette notation prête à confession. La raison en est qu’elle donne à penser qu’il existe un événement conditionnel « » dont on calculerait la probabilité. Il n'existe pas d’événements conditionnels, mais seulement des probabilités conditionnelles, c’est-à-dire d'autres probabilités sur l'espace probabilisable.
- Il est parfois utile de connaître pour calculer . En effet, on a la relation suivante :
Cette formule est connue sous le nom « Formule de Bayes ».
III- Probabilité conditionnelle
3-1/ Introduction
Corollaire
Soit une probabilité définie sur un univers , et soit un événement tel que .
Puisque est une probabilité sur , elle possède toutes les propriétés d’une probabilité.
En particulier, on a :
1)
2) Pour tout événement vérifiant , on a :
3) Pour tout événement :
4) Pour tous événements et :
5) Pour tous événements et :
III- Probabilité conditionnelle
3-2/ Formule des probabilités composées
Proposition 4
Soit une probabilité définie sur un univers .
Pour tous événements et de , on a la formule suivante dite « Formule des probabilités composées » :
III- Probabilité conditionnelle
3-3/ Formule des probabilités totales
Proposition 5
Soit une probabilité définie sur un univers , et soit un système complet d’événements de .
Pour tout événement , on a la formule suivante dite « Formule des probabilités
totales » :
Si, pour tout , on a , on obtient :
III- Probabilité conditionnelle
3-3/ Formule des probabilités totales
Corollaire
Soit une probabilité définie sur un univers .
Pour tous événements et de , on a :
Si , on obtient :


