Séance 14 - Géométrie dans l'espace

Sommaire

I- Les axiomes de l’espace

II- Détermination d’un plan

III- Positions relatives dans l’espace

3-1/ Positions relatives de deux droites

3-2/ Positions relatives d’une droite et d’un plan

3-3/ Positions relatives de deux plans

IV- Parallélisme dans l’espace

4-1/ Parallélisme de deux droites

4-2/ Parallélisme d’une droite et un plan

4-3/ Parallélisme de deux plans

V- Orthogonalité dans l’espace

5-1/ Orthogonalité de deux droites

5-2/ Orthogonalité d’une droite et un plan

5-3/ Orthogonalité de deux plans

VI- Surfaces et volumes de certains solides

VII- Exercices

7-1/ Exercice 1

7-2/ Exercice 2

7-3/ Exercice 3

7-4/ Exercice 4

I- Les axiomes de l’espace

Axiome 1

Par deux points distincts $A$ et $B$ de l’espace $\left(\mathcal{E}\right)$ passe une et une seule droite notée $\left(AB\right)$.

Axiome 2

Par trois points non alignés de l’espace $\left(\mathcal{E}\right)$ passe un plan et un seul noté $\left(ABC\right)$.

Axiome 3

Si A et B sont deux points distincts d’un plan (P) de l’espace $\left(\mathcal{E}\right)$, alors la droite $\left(AB\right)$ est incluse dans le plan $\left(P\right)$.

Axiome 4

$\left(P\right)$ et $\left(P\text{'}\right)$ sont deux plans distincts de l’espace $\left(\mathcal{E}\right)$.

Si un point $A$ est commun aux deux plans, alors les deux plans se coupent suivant une droite passant par le point $A$.

II- Détermination d’un plan

Toutes les propriétés de la géométrie plane reste valables à chaque plan $\left(P\right)$ de l’espace $\left(\mathcal{E}\right)$.

Un plan $\left(P\right)$ est déterminé soit par :

1. Une droite $\left(D\right)$ et un point qui n’appartienne pas à cette droite $\left(A\notin \left(D\right)\right)$.
2. Trois points $A$ et $B$ et $C$ non alignés de l’espace $\left(\mathcal{E}\right)$.
3. Deux droites $\left(D\right)$ et $\left(D\text{'}\right)$ sécantes de l’espace $\left(\mathcal{E}\right)$.
4. Deux droites $\left(D\right)$ et $\left(D\text{'}\right)$ strictement parallèles de l’espace $\left(\mathcal{E}\right)$.

III- Positions relatives dans l’espace

3-1/ Positions relatives de deux droites

Cas 1 : $\left(D\right)$ et $\left(D\text{'}\right)$ sont sécantes au point $I : \left(\left(D\right)\cap \left(D\text{'}\right)=\left\{I\right\}\right)$

Cas 2 : $\left(D\right)$ et $\left(D\text{'}\right)$ sont parallèles : $\left(D\right)//\left(D\text{'}\right)$

Cas 3 : $\left(D\right)$ et $\left(D\text{'}\right)$ sont non coplanaires : $\left(D\right)\cap \left(D\text{'}\right)=\varnothing$

III- Positions relatives dans l’espace

3-2/ Positions relatives d’une droite et d’un plan

Cas 1 : $\left(D\right)$ est incluse dans le plan $\left(P\right)$ : $\left(D\right)\subset \left(P\right)$

$\left(D\right)\cap \left(P\right)=\left(D\right)$

Cas 2 : $\left(D\right)$ et $\left(P\right)$ sont strictement parallèles : $\left(D\right)//\left(P\right)$

$\left(D\right)\cap \left(P\right)=\varnothing$

Cas 3 : $\left(D\right)$ coupe le plan $\left(P\right)$ au point $I$

$\left(D\right)\cap \left(P\right)=\left\{I\right\}$

III- Positions relatives dans l’espace

3-3/ Positions relatives de deux plans

Cas 1 : $\left(P\right)$ et $\left(P\text{'}\right)$ sont confondus : $\left(P\right)=\left(P\text{'}\right)$

$\left(P\right)\cap \left(P\text{'}\right)=\left(P\right)$

Cas 2 : $\left(P\right)$ et $\left(P\text{'}\right)$ sont strictement parallèles : $\left(P\right)//\left(P\text{'}\right)$

$\left(P\right)\cap \left(P\text{'}\right)=\varnothing$

Cas 3 :$\left(P\right)$ et $\left(P\text{'}\right)$ sont sécants suivant une droite $\left(D\right)$

$\left(P\right)\cap \left(P\text{'}\right)=\left(D\right)$

IV- Parallélisme dans l’espace

4-1/ Parallélisme de deux droites

Définition

Deux droites $\left(D\right)$ et $\left(D\text{'}\right)$ de l’espace sont parallèles si et seulement si :

• $\left(D\right)$ et $\left(D\text{'}\right)$ sont coplanaires disjointes.

Ou

• $\left(D\right)$ et $\left(D\text{'}\right)$ sont confondues.

On note $\left(D\right)//\left(D\text{'}\right)$

IV- Parallélisme dans l’espace

4-1/ Parallélisme de deux droites

Propriétés

1- D’un point $O$ de l’espace passe une et une seule droite $\left(\Delta \right)$ parallèle a une droite $\left(D\right)$ donnée de l’espace.

2- Soient $\left(D\right)$, $\left(D\text{'}\right)$ et $\left(\Delta \right)$ trois droites de l’espace $\left(\mathcal{E}\right)$.

- Si $\left(D\right)$ et $\left(D\text{'}\right)$ sont parallèles et une droite $\left(\Delta \right)$ est parallèle à l’une des deux droites, alors $\left(\Delta \right)$ est parallèle à l’autre droite :

$\left\{\begin{array}{l}\left(D\right)//\left(D\text{'}\right)\\ \left(\Delta \right)//\left(D\right)\end{array}\right.\Rightarrow \left(\Delta \right)//\left(D\text{'}\right)$

- Si une droite $\left(\Delta \right)$ est parallèle à chacune des droites $\left(D\right)$ et $\left(D\text{'}\right)$, alors $\left(D\right)$ et $\left(D\text{'}\right)$ sont parallèles :

$\left\{\begin{array}{l}\left(\Delta \right)//\left(D\text{'}\right)\\ \left(\Delta \right)//\left(D\right)\end{array}\right.\Rightarrow \left(D\right)//\left(D\text{'}\right)$

IV- Parallélisme dans l’espace

4-2/ Parallélisme d’une droite et un plan

Définition

Une droite $\left(D\right)$ est parallèle à un plan $\left(P\right)$ si et seulement si :

• La droite $\left(D\right)$ est un incluse dans le plan $\left(P\right)$ : $\left(D\right)\subset \left(P\right)$

Ou

• $\left(D\right)$ et $\left(P\right)$ sont disjoints : $\left(D\right)\cap \left(P\text{'}\right)=\varnothing$

IV- Parallélisme dans l’espace

4-2/ Parallélisme d’une droite et un plan

Propriété

Une droite $\left(D\right)$ est parallèle à un plan $\left(P\right)$ si et seulement si : il existe une droite $\left(D\text{'}\right)$ incluse dans le plan $\left(P\right)$ tel que $\left(D\right)$ et $\left(D\text{'}\right)$ sont parallèles.

IV- Parallélisme dans l’espace

4-3/ Parallélisme de deux plans

Définition

Deux plans $\left(P\right)$ et $\left(P\text{'}\right)$ sont parallèles si et seulement si :

• $\left(P\right)$ et $\left(P\text{'}\right)$ sont confondus : $\left(P\right)=\left(P\text{'}\right)$

Ou

• $\left(P\right)$ et $\left(P\text{'}\right)$ sont disjoints : $\left(P\right)\cap \left(P\text{'}\right)=\varnothing$

IV- Parallélisme dans l’espace

4-3/ Parallélisme de deux plans

Propriétés

1- D’un point $O$ de l’espace passe un et un seul plan $\left(P\text{'}\right)$ parallèle a un plan $\left(P\right)$ donné de l’espace.

2- Si deux plans $\left(P\right)$ et $\left(P\text{'}\right)$ sont parallèles, alors tout plan $\left(Q\right)$ parallèle à l’un des deux plans est parallèle à l’autre plan.

3- Si un plan $\left(Q\right)$ est parallèle à chacun des plans $\left(P\right)$ et $\left(P\text{'}\right)$, alors les deux plans $\left(P\right)$ et $\left(P\text{'}\right)$ sont parallèles.

4- Deux plans $\left(P\right)$ et $\left(P\text{'}\right)$ sont parallèles si et seulement si l’un d’eux contient deux droites sécantes $\left(D\right)$ et $\left(D\text{'}\right)$ parallèles au deuxième plan :

IV- Parallélisme dans l’espace

4-3/ Parallélisme de deux plans

Propriétés

1- Si deux plans$\left(P\right)$ et $\left(P\text{'}\right)$ sont parallèles, alors toute droite $\left(D\right)$  qui coupe l’un des deux plans coupe l’autre plan :

2- Si deux plans $\left(P\right)$ et $\left(P\text{'}\right)$ sont parallèles, alors tout plan $\left(Q\right)$ qui coupe l’un des deux plans suivant une droite $\left(\Delta \right)$  coupe l’autre plan suivant une droite $\left(\Delta \text{'}\right)$ et les droites sont parallèles :

3- Si une droite $\left(D\right)$ est strictement parallèle à deux plans sécants $\left(P\right)$ et $\left(P\text{'}\right)$ suivant une droite $\left(\Delta \right)$, alors les deux droites $\left(D\right)$ et $\left(\Delta \right)$ sont parallèles :

V- Orthogonalité dans l’espace

5-1/ Orthogonalité de deux droites

Définition

$\left(D\right)$ et $\left(\Delta \right)$ deux droites sont orthogonales si et seulement si deux droites $\left(D\text{'}\right)$ et $\left(\Delta \text{'}\right)$ sont sécantes à un point $A$ de l’espace et orthogonales tel que $\left(D\right)//\left(D\text{'}\right)$ et $\left(\Delta \right)//\left(\Delta \text{'}\right)$.

On note : $\left(\Delta \right)\perp \left(D\right)$.

V- Orthogonalité dans l’espace

5-1/ Orthogonalité de deux droites

Propriétés

Si deux droites $\left(D\right)$ et $\left(D\text{'}\right)$ sont orthogonales, alors toute droite $\left(\Delta \right)$ parallèle à l’une de ces deux droites est orthogonale à l’autre droite.

Si deux droites $\left(D\right)$ et $\left(D\text{'}\right)$ sont parallèles, alors toute droite $\left(\Delta \right)$ orthogonale à l’une des deux droites est orthogonale à l’autre droite.

V- Orthogonalité dans l’espace

5-2/ Orthogonalité d’une droite et un plan

Définition

Une droite $\left(D\right)$ est orthogonale à un plan $\left(P\right)$ de l’espace si et seulement si la droite $\left(D\right)$ est orthogonale à toute droite $\left(\Delta \right)$ du plan $\left(P\right)$.

On note : $\left(D\right)\perp \left(P\right)$, et on lit : $\left(D\right)$ est orthogonale au plan $\left(P\right)$.

V- Orthogonalité dans l’espace

5-2/ Orthogonalité d’une droite et un plan

Propriétés

1- Une droite $\left(D\right)$ est orthogonale à un plan $\left(P\right)$ de l’espace si et seulement si la droite $\left(D\right)$ est orthogonale à deux droites sécantes du plan $\left(P\right)$.

2- Si deux droites $\left(D\right)$ et $\left(D\text{'}\right)$ sont parallèles, alors tout plan $\left(P\right)$ orthogonal à l’une de ces deux droites est orthogonal à l’autre droite.

3- Si deux plans $\left(P\right)$ et $\left(P\text{'}\right)$ sont parallèles, alors toute droite $\left(D\right)$ orthogonale à l’un des deux plans est orthogonale à l’autre plan.

V- Orthogonalité dans l’espace

5-3/ Orthogonalité de deux plans

Définition

Deux plans $\left(P\right)$ et $\left(P\text{'}\right)$ de l’espace $\left(\mathcal{E}\right)$ sont orthogonaux si et seulement si l’un des deux plans contient une droite $\left(D\right)$ orthogonale à l’autre plan.

On note : $\left(P\right)\perp \left(P\text{'}\right)$

V- Orthogonalité dans l’espace

5-3/ Orthogonalité de deux plans

Propriétés

1- Si deux plans $\left(P\right)$ et $\left(P\text{'}\right)$ de l’espace $\left(\mathcal{E}\right)$ sont orthogonaux à une même droite, alors les plans sont parallèles.

2- Si deux plans $\left(P\right)$ et $\left(P\text{'}\right)$ de l’espace $\left(\mathcal{E}\right)$ sont parallèles :

• Si un plan $\left(Q\right)$ est orthogonal à l’un des deux plans, alors $\left(Q\right)$ est orthogonal à l’autre.
• Si une droite $\left(D\right)$ est orthogonale à l’un des deux plans, alors $\left(D\right)$ est orthogonale à l’autre.

3- Pour tout plan $\left(Q\right)$ orthogonal à deux plans sécants $\left(P\right)$ et $\left(P\text{'}\right)$ suivant une droite $\left(D\right)$, on a : $\left(D\right)\perp \left(Q\right)$.

VI- Surfaces et volumes de certains solides

Cube	Parallélépipède rectangle
Aire (surface) latérale : $S_L=4a^2$ Aire (surface) totale : $S_T=6a^2$ Volume : $V=a^3$	Aire (surface) latérale : $S_L=2\left(L+l\right)\times h$ Aire (surface) totale : $S_T=S_L+2L\times l$ Volume : $V=L\times l\times h$
Cylindre droit	Cône de révolution
Aire (surface) latérale : $S_L=2\mathrm{\pi }\times \mathrm{R}\times \mathrm{h}$ Volume : $V=\mathrm{\pi }\times {\mathrm{R}}^2\times \mathrm{h}$	Volume : $V=\frac{1}{3}\mathrm{\pi }\times {\mathrm{R}}^2\times \mathrm{h}$
Pyramide	Prisme droit
Surface de la base : $S_H$ Volume : $V=\frac{1}{3}{S}_H\times h$	Périmètre de la base : $P_B$ Surface de la base : $S_B$ Aire (surface) latérale : $S_L=P_B\times h$ Volume : $V=S_B\times h$

Sphère

Rayon : $R$

Volume : $V=\frac{4}{3}\mathrm{\pi }\times {\mathrm{R}}^3$

VII- Exercices

7-1/ Exercice 1

Dans un tétraèdre $ABCD$, $I$ est un point de l’arête $\left[AB\right]$ et $J$ est un point de l’arête $\left[CD\right]$.

Le but de l’exercice est de trouver l’intersection des plans $\left(AJB\right)$ et $\left(CID\right)$.

1. Prouver que chacun des points $I$ et $J$ appartient à la fois aux plans $\left(AJB\right)$ et $\left(CID\right)$.

2. Quelle est alors l’intersection de ces deux plans.

VII- Exercices

7-2/ Exercice 2

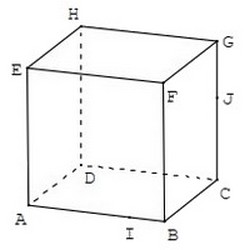
On considère un cube $ABCDEFGH$, $I$ est un point de l’arête $\left[AB\right]$ et $J$ est un point de l’arête $\left[CG\right]$.

1. Montrer que les points $I$ et $J$ appartiennent à la fois aux plans $\left(ABJ\right)$ et $\left(CGI\right)$.

2. Quelle est l’intersection des plans $\left(ABJ\right)$ et $\left(CGI\right)$ ?

VII- Exercices

7-3/ Exercice 3

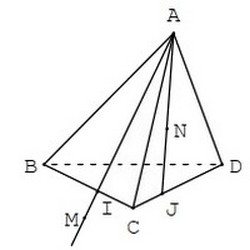
$ABCD$ est un tétraèdre, $I$ est un point de l’arête $\left[BC\right]$ et $J$ un point de l’arête $\left[CD\right]$.

$N$ est un point du segment $\left[AJ\right]$ et $M$ un point de la demi-droite $\left[AI\right)$ extérieur au segment $\left[AI\right]$.

1. Quelle est l’intersection des plans $\left(AIJ\right)$ et $\left(BCD\right)$ ?

2. Démontrer que les points $M$, $N$, $I$ et $J$ sont dans un même plan.

On note $P$ le point d’intersection de la droite $\left(MN\right)$ et du plan $\left(BCD\right)$.

3. Prouver que $P$ est sur $\left(IJ\right)$.

VII- Exercices

7-4/ Exercice 4

$ABCDEFGH$ est un cube, $I$ est le milieu de $\left[AB\right]$.

On se propose de représenter la droite $\left(\Delta \right)$ d’intersection des plans $\left(DIF\right)$ et $\left(EFG\right)$.

1. Pourquoi $F$ appartient-il à $\left(\Delta \right)$ ?

2. Quelle est l’intersection des plans $\left(DIF\right)$ et $\left(ABC\right)$?

3. Que sait-on sur les plans $\left(ABC\right)$ et $\left(EFG\right)$ ? En déduire la droite $\left(\Delta \right)$.