Séance 22 - Le champ magnétique créé par un courant électrique

Sommaire

I- Champ magnétique créé par un fil rectiligne

1-1/ Spectre magnétique et lignes de champs magnétiques

1-2/ Caractéristiques du vecteur champ magnétique

II- Champ magnétique créé par un conducteur circulaire (bobine plate)

2-1/ Définition

2-2/ Spectre magnétique et lignes de champs magnétiques

2-3/ Caractéristiques du vecteur champ magnétique

III- Champ magnétique créé par un solénoïde

3-1/ Définition

3-2/ Spectre magnétique et lignes de champs magnétiques

3-3/ Caractéristiques du vecteur champ magnétique

IV- Exercices

4-1/ Exercice 1

4-2/ Exercice 2

4-3/ Exercice 3

4-4/ Exercice 4

I- Champ magnétique créé par un fil rectiligne

1-1/ Spectre magnétique et lignes de champs magnétiques

Un fil de longueur infinie parcouru par un courant d’intensité $I$, crée un champ magnétique dont les lignes de champ sont des cercles concentriques centrés sur le fil et situé dans le plan perpendiculaire au fil.

I- Champ magnétique créé par un fil rectiligne

1-2/ Caractéristiques du vecteur champ magnétique

Direction

Portée par la tangente au cercle du spectre passant par M.

Sens

Donné par les règles d’orientation :

Intensité

Donnée par la relation : $B=\frac{{\mu }_0}{2\mathrm{\pi }}.\frac{I}{d}$

$B$ : intensité du champ magnétique au point $M$.
${\mu }_0$: perméabilité magnétique du vide (ou de l’aire), sa valeur est ${\mu }_0=4\mathrm{\pi }.{10}^{-7} \left(\mathrm{SI}\right)$
$I$ : intensité du courant.
$d=OM$ : La distance du point $M$ au fil.

Donc : $B=2.{10}^{-7}.\frac{I}{d}$

II- Champ magnétique créé par un conducteur circulaire (bobine plate)

2-1/ Définition

Une bobine est constituée d’un enroulement de fil conducteur sur un cylindre de rayon $r$.

Si la longueur de la bobine $L$ est faible par rapport à son rayon $R$, on a une bobine plate.

II- Champ magnétique créé par un conducteur circulaire (bobine plate)

2-2/ Spectre magnétique et lignes de champs magnétiques

Dans un plan perpendiculaire au plan de la bobine et contenant son centre, les lignes de champ sont des droites rectilignes près du centre et s’incurvent en s’éloignant de celui-ci pour devenir des cercles fermés près des fils conducteurs.

II- Champ magnétique créé par un conducteur circulaire (bobine plate)

2-3/ Caractéristiques du vecteur champ magnétique

Sens

Le sens du vecteur champ magnétique est déterminé par la règle du bonhomme d’Ampère ou de la main droite.

• La face nord de la bobine est la face par laquelle sortent les lignes de champ.
• La face sud de la bobine est la face par laquelle entrent les lignes de champ.

On regarde l’une des faces :

• s’il correspond au sens indiqué par la lettre S on regarde sur la face sud.
• s’il correspond à celui indiqué par la lettre N on regarde sur la face nord.

Intensité

L’intensité du champ magnétique crée par une bobine plate de rayon $R$, contenant $N$ spires et parcouru par un courant continu $I$ en son centre $O$ est : $B=\frac{{\mu }_0}{2}\frac{N.I}{R}$

III- Champ magnétique créé par un solénoïde

3-1/ Définition

Un solénoïde est constitué d’un fil conducteur enroulé régulièrement en hélice de façon à former une bobine dont la longueur est grande par rapport à son rayon.

Si $L$ et $R$ sont du même ordre de grandeur on a une bobine.

Si $L>10R$ on a un solénoïde infini.

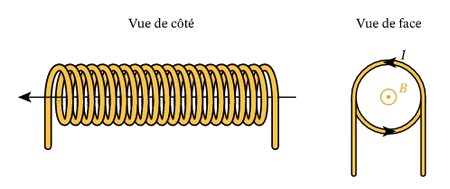
III- Champ magnétique créé par un solénoïde

3-2/ Spectre magnétique et lignes de champs magnétiques

À l’intérieur d’un solénoïde les lignes de champ sont des droites parallèles, le champ est donc uniforme.

À l’extérieur du solénoïde, le spectre magnétique ressemble à celui d’un aiment droit.

III- Champ magnétique créé par un solénoïde

3-3/ Caractéristiques du vecteur champ magnétique

Sens

Règle de la main droite (valable dans tous les cas) :

• Pouce : sens de $\overrightarrow{B}$
• Doigts courbés : sens du courant $I$

Intensité

A l’intérieur du solénoïde le champ magnétique est uniforme d’intensité :

$B={\mu }_0.\frac{N}{L}.I={\mu }_0.n.I$

$n=\frac{N}{L}$ : densité de spires, avec $L$ (longueur du solénoïde) et $N$ (nombre de spires).

IV- Exercices

4-1/ Exercice 1

Le schéma suivant représente un aimant droit qui crée un champ magnétique.

On place une aiguille aimantée au point $M$ qui indique ce champ magnétique qu’a pour valeur $B_1=3.{10}^{-3}T$ :

On approche du point $M$ une bobine, son axe est perpendiculaire à l’axe de l’aimant, lorsque un courant $I$ traverse la bobine l’aiguille se dévie d’un angle $\alpha =30°$ :

1. Comment on explique la déviation de l’aiguille ?

2. Déterminer les caractéristiques du champ magnétique indiqué par l’aiguille.

3. Calculer l’intensité du champ magnétique créé par la bobine.

4. Sur la figure, déterminer le sens du courant électriques dans la bobine.

IV- Exercices

4-2/ Exercice 2

Soit un solénoïde de longueur $L$ et de nombre de spires $N=800$, à l’intérieur du solénoïde se trouve une aiguille aimantée mobile autour d’un pivote vertical passant par son centre d’inertie.

Quand un courant électrique d’intensité $I=20mA$ traverse la bobine, l’aiguille se dévie d’un angle $\theta =45°$ :

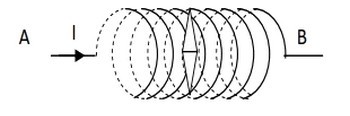
1. Représenter sur le schéma le vecteur champ magnétique créé par le courant à l’intérieur du solénoïde.

2. Représenter sur le schéma le vecteur champ magnétique indiqué par l’aiguille.

3. Déterminer les caractéristiques du champ magnétique créé par le courant.

4. Déduire la valeur de $L$.

5. Déterminer les caractéristiques du champ magnétique total à l’intérieur de solénoïde.

Au voisinage du solénoïde est placé un aimant droit qui crée un champ magnétique sa valeur à la position de l’aiguille est $B\text{'}=3.{10}^{-6}T$ :

6. Calculer la valeur du champ magnétique indiqué par l’aiguille.

7. Calculer l’angle que forme l’aiguille avec l’horizontale.

On donne la composante tangentielle du champ terrestre $B_H=2.{10}^{-5}T$.

IV- Exercices

4-3/ Exercice 3

On pose un aimant droit à côté d'un fil conducteur rectiligne de longueur infini tel que le fil est perpendiculaire au plan qui contient aimant.

Le fil est parcouru par un courant d’intensité $I=15A$ dont le sens est indiqué dans la ligure :

L’aimant crée en un point $M$ distant du fil de $d=2cm$, un champ magnétique d’intensité $B_2=4.{10}^{-4}T$.

1. Calculer $B_1$ l’intensité du champ magnétique crée par le courant électrique traversant le fil conducteur au point $M$.

2. Représenter sur la figure (sans échelle) au point $M$ le vecteur $\overrightarrow{B_1}$ du champ magnétique crée par le courant électrique traversant le fil conducteur, le vecteur $\overrightarrow{B_2}$ du champ magnétique crée par l’aimant, et le vecteur $\overrightarrow{B_T}$ du champ magnétique total au point $M$.

3. Déterminer par calcul $B_T$ l’intensité du champ magnétique total au point $M$.

4. Calculer l'angle $\alpha =\left(\overrightarrow{B_1};\overrightarrow{B_T}\right)$.

IV- Exercices

4-4/ Exercice 4

On considère deux barreaux aimantés $A_1$ et $A_2$ posés sur le même alignement avec un point $M$ comme l’indique la figure suivante :

Les intensités des champs magnétiques créés par $A_1$ et $A_2$ au point $M$ sont : $B_1=20mT$ et $B_2=30mT$.

1. Représenter les vecteurs champ magnétique en utilisant l'échelle suivante $\left(1cm\to 10mT\right)$. Puis représenter le vecteur champ magnétique globale au point $M$.

2. Déterminer graphiquement puis par calcul l'intensité du champ magnétique $\overrightarrow{B}$ global au point $M$, puis déterminer l’angle que forme $\overrightarrow{B}$ avec le plan horizontal (on néglige le champ magnétique terrestre).

On considère une bobine de rayon $R=2,5cm$ et de longueur $L=60cm$ composée de $N=600 spires$ et parcourue par un courant électrique d'intensité $I=239mA$ comme l'indique la figure suivante :

3. Donner la définition d'un solénoïde.

4. Montrer que la bobine précédente peut être considérée comme un solénoïde.

5. Déterminer l'intensité du champ magnétique crée par ce solénoïde.

6. Préciser la nature de chacune des faces du solénoïde.

7. Préciser les pôles de l'aiguille aimantée.

8. Déterminer le sens et la direction du champ magnétique $\overrightarrow{B}$ créé par le solénoïde à son intérieur.

9. Représenter le spectre du champ magnétique créé par le solénoïde.

Le diamètre du fil enroulé est $d=2mm$.

10. Quelle est le nombre de couches enroulées sur le cylindre formant le solénoïde ?