
Mathématiques : Tronc Commun
Séance 12 (Transformations du plan)
Professeur : Mr ETTOUHAMY Abdelhak
Sommaire
I- Transformations dans le plan
II- Symétrie axiale
III- Symétrie centrale
IV- Translation
V- Homothétie
VI- Propriétés caractéristiques de , et
6-1/ Propriétés
6-2/ Les images de certaines figures géométriques par les transformations
6-3/ Tableau récapitulatif
VII- Exercices
7-1/ Exercice 1
7-2/ Exercice 2
7-3/ Exercice 3
7-4/ Exercice 4
I- Transformations dans le plan
Définition
Toute relation qui associe à tout point du plan au point de tel que vérifie une ou plusieurs conditions, on l’appelle transformation du plan , on la note ou ou ou ....
On écrit
On dit que le point a pour image par la transformation , ou encore le point est l’image du point .
Exemple
Soient et deux points du plan .
Soit la transformation du plan définie par tel que
II- Symétrie axiale
Définition
La symétrie axiale de droite du plan est la transformation qui transforme tout point de au point tel que la droite soit la médiatrice du segment .
On écrit
Exemple
III- Symétrie centrale
Définition
La symétrie centrale de centre le point du plan est la transformation qui transforme tout point de au point tel que le point soit le milieu du segment .
On écrit
Exemple
Remarques
équivaut à
équivaut à
est le seul point invariant par la symétrie centrale , d’où .
IV- Translation
Définition
La translation du vecteur du plan est la transformation qui transforme tout point de au point tel que le point .
On note la translation par
On écrit :
Exemple
Remarques
équivaut à le quadrilatère est parallélogramme (avec )
équivaut à
équivaut à
Si aucun point de est invariant.
Tous les points du plan sont invariant par la translation de vecteur nul
V- Homothétie
Définition
L’homothétie de centre un point donné du plan et de rapport est la transformation qui transforme tout point de au point tel que .
On note l’homothétie par
On écrit :
Exemple
Remarques
Si , ona et et sont alignés.
Si , on a (tous les points ont pour image - l’homothétie n’est pas intéressante).
Si , on a (tous les points sont invariants - l’homothétie n’est pas intéressante).
Pour cela on prend
Si , on a ' avec est le milieu de , l’homothétie est la symétrie centrale , ou encore .
Si , on a ' avec .
Si , on a ' avec appartienne à la demi droite opposée à .
VI- Propriétés caractéristiques de ,
6-1/ Propriétés
Soit une transformation dans le plan tel que pour tous points et de on a et .
- La transformation est une translation si et seulement si .
- La transformation est une homothétie si et seulement si et
VI- Propriétés caractéristiques de , et
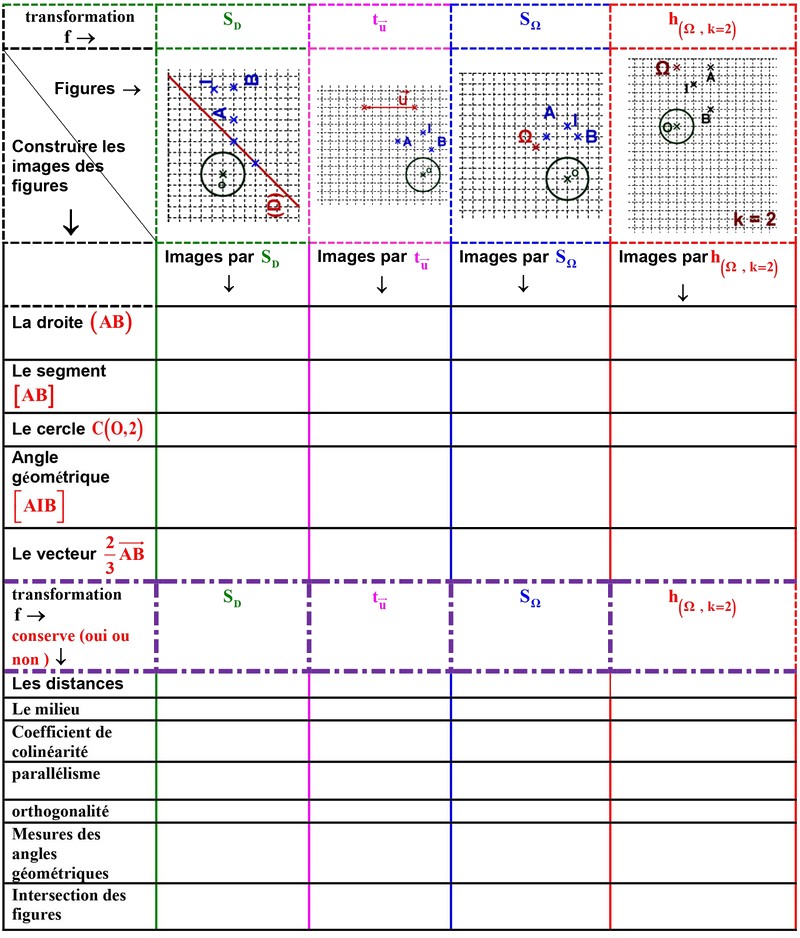
6-2/ Les images de certaines figures géométriques par les transformations
Soient et deux points du plan et et leurs images par l’une des transformations suivantes : symétrie axiale ou symétrie centrale ou translation ou homothétie .
1- L’mage de la droite par les transformations précédentes est la droite , et .
2- L’mage du segment par les transformations précédentes est le segment , et , sauf l’homothétie .
3- L’mage du vecteur par les transformations précédentes est le vecteur , sauf l’homothétie .
4- L’mage du cercle par les transformations précédentes est le cercle , sauf l’homothétie (le cercle ).
5- L’mage de l’angle géométrique par les transformations précédentes est l’angle géométrique de mêmes mesure .
6- Les transformations précédentes conservent les distance ( sauf l’homothétie ), et le milieu, et les mesures des angles géométriques, et le coefficient de colinéarité, et le parallélisme, et l’orthogonalité, et l’intersection des figures.
VI- Propriétés caractéristiques de , et
6-3/ Tableau récapitulatif
VII- Exercices
7-1/ Exercice 1
Soit un vecteur du plan.
est un quadrilatère du plan tel que est l’image de par la translation de vecteur et est l’image de par la translation de vecteur .
- Montrer que : .
Soit le milieu du segment .
- Monter que est un parallélogramme.
est un triangle.
Pour tout point du plan on considère le tel que
- Montrer que est l’image de par une translation de vecteur à préciser.
VII- Exercices
7-2/ Exercice 2
- Exprimer vectoriellement la proposition suivante : est l’image de par l’homothétie de centre et de rapport .
- Exprimer la relation vectorielle par une homothétie.
- Déterminer le centre et le rapport de l’homothétie qui transforme en dans les cas suivants :
Soient et deux points du plan .
Soit la transformation plane qui à tout point associe le point tel que .
- Montrer que a un unique point invariant .
- Exprimer en fonction de .
- En déduire la nature de la transformation .
VII- Exercices
7-3/ Exercice 3
est un rectangle.
On considère la translation de vecteur .
Soient , , et les images respectives de , , et par .
- Montrer que est un rectangle.
On considère les points et du plan définis par et
- Montrer que .
VII- Exercices
7-4/ Exercice 4
est un parallélogramme et et sont deux points du plan tels que et .
- Construire une figure convenable.
- Montrer que la droite est l’image de la droite par la translation de vecteur .
Soit l’homothétie de centre et qui transforme en .
- Montrer que le rapport de est .
Soit l’image de par .
- Montrer que


