Séance 11 - Généralités sur les fonctions

Sommaire

I- Généralités sur les fonctions numériques

1-1/ Fonction numérique d’une variable numérique

1-2/ Représentation graphique (ou courbe représentative) d’une fonction numérique

1-3/ Égalité de deux fonctions

II- Fonction paire – fonction impaire

2-1/ Fonction paire

2-2/ Fonction impaire

III- Sens de variation d’une fonction

IV- Taux d’accroissement d’une fonction

V- Extremums d’une fonction

VI- Étude de certains fonctions

6-1/ Fonction $f\left(x\right)=a{x}^2 \left(a\ne 0\right)$

6-2/ Fonction $f\left(x\right)=\frac{a}{x} \left(a\ne 0\right)$

6-3/ Fonction $f\left(x\right)=a{x}^2+bx+c \left(a\ne 0\right)$

6-4/ Fonction $f\left(x\right)=\frac{ax+b}{cx+d} \left(ad-bc\ne 0\right)$

VII- Exercices

7-1/ Exercice 1

7-2/ Exercice 2

7-3/ Exercice 3

7-4/ Exercice 4

I- Généralités sur les fonctions numériques

1-1/ Fonction numérique d’une variable numérique

Vocabulaire

La relation qui nous permet de lier chaque élément $x\in \mathrm{ℝ}$ par un seul élément $y\in \mathrm{ℝ}$  est appelée fonction numérique de la variable réelle $x$ définie de $\mathrm{ℝ}$ vers $\mathrm{ℝ}$.

On la note par $f$ ou $g$ ou $h$ …

•  $y=f\left(x\right)$ est l’image de $x$ par $f$.
•  $x$ est un antécédent de $y$ par $f$.

Si l’image de $x$ existe, on dit que la fonction $f$ est définie en $x$.

Tous les réels $x$ qui ont des images par la fonction $f$ constituent un ensemble appelé ensemble de définition ou domaine de définition, on le note par $D$ ou $D_f$.

I- Généralités sur les fonctions numériques

1-2/ Représentation graphique (ou courbe représentative) d’une fonction numérique

Définition

Soit $f$ une fonction numérique de la variable réelle $x$ définie sur $D_f\left(D_f\subset \mathrm{ℝ}\right)$

Le plan $\left(P\right)$ est rapporté au repère $\left(O,\overrightarrow{i},\overrightarrow{j}\right)$.

On appelle courbe représentative de la fonction $f$, notée $\left(C_f\right)$ ou ${\mathcal{C}}_f$, l’ensemble des points $M$ de $\left(P\right)$
de coordonnées $\left(x,f\left(x\right)\right)$ où $x\in D_f$.

Un point $M\left(x,y\right)\in \left(C_f\right)$ équivaut à $x\in D_f$ et $y=f\left(x\right)$.

La relation $y=f\left(x\right)$ s’appelle équation cartésienne de la courbe $\left(C_f\right)$ dans le repère $\left(O,\overrightarrow{i},\overrightarrow{j}\right)$.

I- Généralités sur les fonctions numériques

1-3/ Égalité de deux fonctions

Définition

Soient $f$ et $g$ deux fonctions définies respectivement sur $D_f$ et $D_g$.

On dit que les deux fonctions $f$ et $g$ sont égales si et seulement si :

• $D_f=D_g$
• Pour tout $x$ de $D_f$ on a : $f\left(x\right)=g\left(x\right)$

Dans ce cas on écrit : $f=g$

Remarque

Si $f=g$, alors les courbes $\left(C_f\right)$ et $\left(C_g\right)$ de $f$ et $g$ sont confondues.

II- Fonction paire – fonction impaire

2-1/ Fonction paire

Définition

Soit $f$ une fonction numérique de la variable réelle $x$ définie sur $D_f$.

On dit que $f$ est une fonction paire sur $D_f$ si et seulement si pour tout $x$ de $D_f$ on a :

• $-x$ est aussi un élément de $D_f$.
• $f\left(-x\right)=f\left(x\right)$( c.à.d. $-x$ et $x$ ont la même image).

II- Fonction paire – fonction impaire

2-1/ Fonction paire

Remarque

La courbe d’une fonction $f$ paire est symétrique par rapport à l’axe des ordonnées.

Si la fonction $f$ est paire sur $D_f$, il suffit de connaître la partie de la courbe $\left(C_f\right)$ tel que les abscisses sont positives, ces abscisses constituent une partie de ${\mathrm{ℝ}}^{+}$ appelée domaine d’étude de la fonction $f$, notée $D_E$.

On a : $D_E=D_f\cap {\mathrm{ℝ}}^{+}$

II- Fonction paire – fonction impaire

2-2/ Fonction impaire

Définition

Soit $f$ une fonction numérique de la variable réelle $x$ définie sur $D_f$.

On dit que $f$ est une fonction impaire sur $D_f$ si et seulement si pour tout $x$ de $D_f$ on a :

• $-x$ est aussi un élément de $D_f$.
• $f\left(-x\right)=-f\left(x\right)$( c.à.d. $-x$ et $x$ ont des images opposées)

II- Fonction paire – fonction impaire

2-2/ Fonction impaire

Remarque

La courbe d’une fonction $f$ impaire est symétrique par rapport à l’origine du repère.

Si la fonction $f$ est impaire sur $D_f$, il suffit de connaître la partie de la courbe $\left(C_f\right)$ tel que les abscisses sont positives, ces abscisses constituent une partie de ${\mathrm{ℝ}}^{+}$ appelée domaine d’étude de la fonction $f$, notée $D_E$.

On a : $D_E=D_f\cap {\mathrm{ℝ}}^{+}$

III- Sens de variation d’une fonction

Définitions

Soit $f$ une fonction numérique de la variable réelle $x$ définie sur $D_f$.

$I$ est un intervalle inclus dans $D_f$.

On dit que $f$ est une fonction croissante sur l’intervalle $I$ si et seulement si pour tous $x$ et $x\text{'}$ de $I$ on a $x<x\text{'}\Rightarrow f\left(x\right)\le f\left(x\text{'}\right)$ (le sens de l’inégalité ne change pas).

On dit que $f$ est une fonction strictement croissante sur l’intervalle $I$ si et seulement si pour tous $x$ et $x\text{'}$ de $I$ on a $x<x\text{'}\Rightarrow f\left(x\right)<f\left(x\text{'}\right)$ (le sens de l’inégalité ne change pas).

On dit que $f$ est une fonction décroissante sur l’intervalle $I$ si et seulement si pour tous $x$ et $x\text{'}$ de $I$ on a $x<x\text{'}\Rightarrow f\left(x\right)\ge f\left(x\text{'}\right)$ (le sens de l’inégalité change ).

On dit que $f$ est une fonction strictement décroissante sur l’intervalle $I$ si et seulement si pour tous $x$ et $x\text{'}$ de $I$ on a $x<x\text{'}\Rightarrow f\left(x\right)>f\left(x\text{'}\right)$ (le sens de l’inégalité change).

On dit que $f$ est une fonction constante sur l’intervalle $I$ si et seulement si pour tous $x$ et $x\text{'}$ de $I$ on a $f\left(x\right)=f\left(x\text{'}\right)$.

III- Sens de variation d’une fonction

Remarque

Si la fonction $f$ est croissante ou bien décroissante sur l’intervalle $I$, on dit que $f$ est monotone sur $I$.

Si la fonction $f$ est strictement croissante ou bien strictement décroissante sur l’intervalle $I$, on dit que $f$ est strictement monotone sur $I$.

Déterminer les variations d’une fonction c’est de rechercher les intervalles sur lesquelles la fonction $f$ est strictement monotone ou constante.

On résume l’ensemble de définition de la fonction $f$ et les variations de la fonction $f$ par un tableau appelé tableau de variation de $f$.

IV- Taux d’accroissement d’une fonction

Définition

Soit $f$ une fonction numérique de la variable réelle $x$ définie sur $D_f$.

$I$ est un intervalle inclus dans $D_f$.

Soient $x$ et $x\text{'}$ de $I$ tel que $x\ne x\text{'}$, le nombre $\frac{f\left(x\right)-f\left(x\text{'}\right)}{x-x\text{'}}$ est appelé le taux d’accroissement de la fonction $f$ entre $x$ et $x\text{'}$, on note $T_f$, d’où $T_f=\frac{f\left(x\right)-f\left(x\text{'}\right)}{x-x\text{'}}$

IV- Taux d’accroissement d’une fonction

Propriété

$T_f$ est le taux d’accroissement de la fonction $f$ sur un intervalle $I$.

• Si $T_f>0$ alors la fonction $f$ est strictement croissante sur l’intervalle $I$.
• Si $T_f<0$ alors la fonction $f$ est strictement décroissante sur l’intervalle $I$.
• Si $T_f=0$ alors la fonction $f$ est constante sur l’intervalle $I$.

V- Extremums d’une fonction

Définition

Soit $f$ une fonction numérique de la variable réelle $x$ définie sur $D_f$.

$I$ est un intervalle inclus dans $D_f$, et $a\in I$.

$f\left(a\right)$ est une valeur maximale de la fonction $f$ sur l’intervalle $I$ équivaut à $f\left(x\right)\le f\left(a\right)$.

$f\left(a\right)$ est une valeur minimale de la fonction $f$ sur l’intervalle $I$ équivaut à $f\left(x\right)\ge f\left(a\right)$.

V- Extremums d’une fonction

Remarque

$f\left(a\right)$ est un extremum de la fonction f signifie que $f\left(a\right)$ est une valeur maximale ou bien  est une valeur minimale de $f$.

Si $f\left(a\right)$ est une valeur maximale de la fonction $f$ sur Df on dit que $f\left(a\right)$ est une valeur maximale absolue de $f$ (sinon on dit que $f\left(a\right)$ est une valeur maximale relative).

Si $f\left(a\right)$ est une valeur minimale de la fonction $f$ sur Df on dit que $f\left(a\right)$ est une valeur minimale absolue de $f$ (sinon on dit que $f\left(a\right)$ est une valeur minimale relative).

VI- Étude de certains fonctions

6-1/ Fonction $f\left(x\right)=a{x}^2 \left(a\ne 0\right)$

Propriété

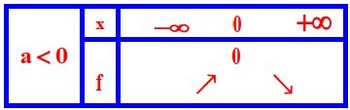
Soit $f$ une fonction numérique de la variable réelle $x$ définie par $f\left(x\right)=a{x}^2 \left(a\ne 0\right)$

La fonction $f$ est paire sur $D_f=\mathrm{ℝ}$.

1er cas : $a>0$	2ème cas : $a<0$
Monotonie de la fonction $f$
La fonction $f$ est strictement croissante sur $[0,+\infty [$ et strictement décroissante sur $]-\infty ,0]$	La fonction $f$ est strictement décroissante sur $[0,+\infty [$ et strictement croissante sur $]-\infty ,0]$
Tableau de variation de la fonction $f$
Courbe représentative de la fonction $f$ dans un repère orthonormé $\left(O,\overrightarrow{i},\overrightarrow{j}\right)$

La courbe représentative de la fonction $f$ est appelée parabole, de sommet l’origine $O$ du repère $\left(O,\overrightarrow{i},\overrightarrow{j}\right)$, d’axe de symétrie l’axe des ordonnées (la droite d’équation $x=0$).

VI- Étude de certains fonctions

6-2/ Fonction $f\left(x\right)=\frac{a}{x} \left(a\ne 0\right)$

Propriété

Soit $f$ une fonction numérique de la variable réelle $x$ définie par $f\left(x\right)=\frac{a}{x} \left(a\ne 0\right)$

La fonction $f$ est impaire sur $D_f=\mathrm{ℝ}*$.

1er cas : $a>0$	2ème cas : $a<0$
Monotonie de la fonction $f$
La fonction $f$ est strictement décroissante sur $[0,+\infty [$ et strictement décroissante sur $]-\infty ,0]$	La fonction $f$ est strictement croissante sur $[0,+\infty [$ et strictement croissante sur $]-\infty ,0]$
Tableau de variation de la fonction $f$
Courbe représentative de la fonction $f$ dans un repère orthonormé $\left(O,\overrightarrow{i},\overrightarrow{j}\right)$

La courbe représentative de la fonction $f$ est appelée hyperbole de centre de symétrie l’origine $O$, d’asymptote horizontale l’axe des abscisses (la droite d’équation $y=0$), et d’asymptote verticale l’axe des ordonnées (la droite d’équation $x=0$).

VI- Étude de certains fonctions

6-3/ Fonction $f\left(x\right)=a{x}^2+bx+c \left(a\ne 0\right)$

Propriété

Soit $f$ une fonction numérique de la variable réelle $x$ définie par $f\left(x\right)=a{x}^2+bx+c \left(a\ne 0\right)$

La fonction $f$ s’écrit de la forme $f\left(x\right)=a{\left(x+\alpha \right)}^2+\beta$ avec $\alpha ,\beta \in \mathrm{ℝ}$

La courbe représentative de la fonction $f$ est un parabole, de sommet le point $S\left(-\alpha ,\beta \right)$, d’axe de symétrie la droite d’équation $x=-\alpha$).

La courbe représentative de la fonction $f$ est obtenue en utilisant la translation du vecteur $\overrightarrow{u}=\alpha \overrightarrow{i}+\beta \overrightarrow{j}$ de la courbe $f\left(x\right)=a{x}^2$.

VI- Étude de certains fonctions

6-4/ Fonction $f\left(x\right)=\frac{ax+b}{cx+d} \left(ad-bc\ne 0\right)$

Propriété

Soit $f$ une fonction numérique de la variable réelle $x$ définie par $f\left(x\right)=\frac{ax+b}{cx+d} \left(ad-bc\ne 0\right)$

La fonction $f$ s’écrit de la forme $f\left(x\right)=\beta +\frac{k}{x+\alpha }$ avec $k,\alpha ,\beta \in \mathrm{ℝ}$ et $x\ne \alpha$

La courbe représentative de la fonction $f$ est un hyperbole, de centre de symétrie le point $S\left(-\alpha ,\beta \right)$, d’asymptote horizontale la droite d’équation $y=\beta$, et d’asymptote verticale la droite d’équation $x=-\alpha$.

La courbe représentative de la fonction $f$ est obtenue en utilisant la translation du vecteur $\overrightarrow{u}=\alpha \overrightarrow{i}+\beta \overrightarrow{j}$ de la courbe $f\left(x\right)=\frac{k}{x}$.

VII- Exercices

7-1/ Exercice 1

Soit $f$ une fonction numérique définie par $f\left(x\right)=2x^2-3$

1. Déterminer les images des nombres suivants $1 ; -1 ; \frac{1}{2} ; \sqrt{5} ; -2$ par la fonction $f$.

2. Déterminer l’ensemble de définition de fonctions suivantes :

3. Comparer les fonctions suivantes :

$$\begin{gathered} \overline{)1} f_1\left(x\right)=x et g_1\left(x\right)=\frac{x^2}{x} \\ \overline{)2} f_2\left(x\right)=\frac{1}{\sqrt{x}-2} et g_2\left(x\right)=\frac{\sqrt{x}+2}{x-4} \end{gathered}$$

VII- Exercices

7-2/ Exercice 2

La figure suivante présente la courbe d’une fonction :

1. Déterminer $D_f$ l’ensemble de définition de $f$.

2. Déterminer les images des nombres suivants : $-5 ; -4 ; -3 ; -2 ; 0 ; 4$

3. Déterminer les antécédents de $5$ et $3$.

4. Étudier la parité de fonctions suivantes :

$$\begin{gathered} \overline{)1} f_1:x\mapsto \left|x\right|-\frac{1}{x^2} \\ \overline{)2} f_2:x\mapsto \frac{x}{x^2-1} \\ \overline{)3} f_3:x\mapsto x^2+x-3 \\ \overline{)4} f_4:x\mapsto \left|x-1\right|-\left|x+1\right| \end{gathered}$$

VII- Exercices

7-3/ Exercice 3

Partie 1

La courbe $\left(C_f\right)$ suivante est la courbe d’une fonction $f$, on précise de plus que $f(3,5)=0$.

1. Déterminer $D_f$ l’ensemble de définition de $f$.

2. Dresser le tableau de variation de $f$.

3. Résoudre graphiquement les inéquations $f\left(x\right)\ge 0$ et $f\left(x\right)<0$.

4. Résoudre graphiquement l’inéquation : $f\left(x\right)>2$

On considère les fonctions $g$ et $h$ définie par : $g\left(x\right)=\sqrt{f\left(x\right)}$ et $h\left(x\right)=\frac{4x-5\sqrt{x}}{f\left(x\right)}$

5. Donner $D_g$ et $D_h$.

Partie 2

Les fonctions $f$ et $g$ sont définies sur $\mathrm{ℝ}$.

Leurs représentations graphiques sont données dans le graphe suivant :

1. Résoudre graphiquement ce qui suit :

$$\begin{gathered} g\left(x\right)=2 ; f\left(x\right)=7 ; f\left(x\right)=2 ; g\left(x\right)<2 ; f\left(x\right)\ge 2 \\ g\left(x\right)=f\left(x\right) ; g\left(x\right)\ge f\left(x\right) ; g\left(x\right)<f\left(x\right) ; g\left(x\right)\ge 0 \end{gathered}$$

VII- Exercices

7-4/ Exercice 4

Partie 1

Soit $f$ une fonction numérique définie par : $f\left(x\right)=x+\frac{4}{x}$

1. Déterminer $D_f$ l’ensemble de définition de $f$.

2. Montrer que $f$ est impaire.

3. Montrer que si $a$ et $b$ sont deux nombres réel distincts non nuls, alors :

$\frac{f\left(b\right)-f\left(a\right)}{b-a}=\frac{ba-4}{ba}$

4. Étudier les variations de $f$ sur chacun des intervalles $[2,+\infty [$ et $]0,2]$.

5. En déduire les variations de $f$ sur chacun des intervalles $]-\infty ,-2]$ et $[-2,0[$.

6. Dresser le tableau de variations de $f$ sur $D_f$.

Partie 2

Soit $f$ une fonction définie par : $f\left(x\right)=-x^2+2x$

1. Déterminer $D_f$ l’ensemble de définition de $f$.

2. Montrer que $1$ est un maximum de $f$ sur $D_f$.

3. Montrer que si $a$ et $b$ sont deux nombres réel distincts de $D_f$, alors :

$\frac{f\left(b\right)-f\left(a\right)}{b-a}=2-a-b$

4. Étudier les variations de $f$ sur chacun des intervalles $[1,+\infty [$ et $]-\infty ,1]$.

5. Dresser le tableau de variations de $f$ sur $D_f$.

On considère la fonction $g$ définie par : $g\left(x\right)=-x^2+2\left|x\right|$

6. Déterminer $D_g$ l’ensemble de définition de $g$

7. Montrer que pour tout $x$ de ${\mathrm{ℝ}}^{+}$, on a : $g\left(x\right)=f\left(x\right)$

8. En déduire le tableau de variation de $g$.