Séance 7-1-1 : Calcul intégral - Partie 1 (Cours)

Sommaire

I- Intégrale d'une fonction continue sur un segment

1-1/ Intégrale et primitives

1-2/ Expression d'une primitive à l'aide d'une intégrale

1-3/ Interprétation géométrique d'une intégrale

II- Techniques de calcul d’intégrales

2-1/ Utilisation des primitives

2-2/ Intégration par parties

2-3/ Intégration par changement de variable

I- Intégrale d'une fonction continue sur un segment

1-1/ Intégrale et primitives

Définition 1

Soit $f$ une fonction continue sur un intervalle $I$, et soit $a$ et $b$ deux éléments de $I$.

Le nombre $F\left(b\right)-F\left(a\right)$, où $F$ est une primitive de $f$, est appelé l’intégrale de la fonction $f$ de $a$ à $b$, et on le note ${\int }_a^{b}f\left(x\right)dx$.

On écrit alors : ${\int }_a^{b}f\left(x\right)dx={\left[F\left(x\right)\right]}_a^b=F\left(b\right)-F\left(a\right)$

I- Intégrale d'une fonction continue sur un segment

1-1/ Intégrale et primitives

Remarque

${\int }_a^{b}f\left(x\right)dx$ se lit « somme de $f\left(x\right)$ de $a$ et $b$ » ou « intégrale de  de $a$ et $b$ »

Les nombres $a$ et $b$ s'appellent les bornes de cette intégrale.

Dans l'écriture ${\int }_a^{b}f\left(x\right)dx$, la lettre $x$ peut être remplacée par une autre lettre.

Ainsi, on a : ${\int }_a^{b}f\left(x\right)dx={\int }_a^{b}f\left(t\right)dt={\int }_a^{b}f\left(u\right)du=....$

I- Intégrale d'une fonction continue sur un segment

1-1/ Intégrale et primitives

Applications

1. Déterminer la dérivée de la fonction $F:x\mapsto \ln \left(x+\sqrt{x^2+1}\right)$ sur ${\mathrm{ℝ}}^{+}$, puis calculer $L={\int }_0^{\frac{3}{4}}\frac{1}{\sqrt{x^2+1}}dx$.

2. Calculer les intégrales suivantes :

$$\begin{gathered} I={\int }_1^{\sqrt{3}}\frac{dx}{1+x^2} \\ J={\int }_{\frac{1}{e}}^e\frac{{\ln }^{3}x}{x}dx \end{gathered}$$

I- Intégrale d'une fonction continue sur un segment

1-1/ Intégrale et primitives

Propriété 1

Soit $f$ une fonction continue sur un intervalle $I$. Alors on a pour tous $a$, $b$ et $c$ de $I$ :

${\int }_a^{a}f\left(x\right)dx=0$ et ${\int }_a^{b}f\left(x\right)dx=-{\int }_b^{a}f\left(x\right)dx$

${\int }_a^{b}f\left(x\right)dx={\int }_a^{c}f\left(x\right)dx+{\int }_c^{b}f\left(x\right)dx$ (C'est la relation de Chasles pour les intégrales).

I- Intégrale d'une fonction continue sur un segment

1-1/ Intégrale et primitives

Applications

 Calculer les intégrales suivantes :

$$\begin{gathered} A={\int }_0^2\left|3x-4\right|dx \\ B={\int }_{-3}^2\left|x^2-3x-4\right|dx \\ C={\int }_{-\frac{\mathrm{\pi }}{2}}^{\frac{\mathrm{\pi }}{3}}\left|\sin 2x\right|dx \end{gathered}$$

I- Intégrale d'une fonction continue sur un segment

1-1/ Intégrale et primitives

Propriété 2

Soit $f$ et $g$ deux fonctions continues sur un intervalle $I$.

Pour tout $\left(a,b\right)\in I^2$ et pour tout $\lambda \in \mathrm{ℝ}$ :

${\int }_a^b\left(f\left(x\right)+g\left(x\right)\right)dx={\int }_a^{b}f\left(x\right)dx+{\int }_a^{b}g\left(x\right)dx$

et

${\int }_a^b\lambda f\left(x\right)dx=\lambda {\int }_a^{b}f\left(x\right)dx$

I- Intégrale d'une fonction continue sur un segment

1-2/ Expression d'une primitive à l'aide d'une intégrale

Proposition 1

Soit $f$ une fonction continue sur un intervalle $I$ et $a$ un élément de $I$.

La fonction $\phi$ définie sur $I$ par $\phi \left(x\right)={\int }_a^{x}f\left(t\right)dt$ est la primitive de $f$ sur $I$ s'annulant en $a$.

I- Intégrale d'une fonction continue sur un segment

1-2/ Expression d'une primitive à l'aide d'une intégrale

Remarques

1- La fonction $\phi$ citée dans la proposition 1 est dérivable sur $I$ et de plus : $\left(\forall x\in I\right) \phi \text{'}\left(x\right)=f\left(x\right)$

Il s'ensuit donc que pour tout $x_0\in I$ :

$\underset{x\to x_0}{\lim }\frac{1}{x-x_0}{\int }_{x_0}^{x}f\left(t\right)dt=\underset{x\to x_0}{\lim }\frac{\phi \left(x\right)-\phi \left(x_0\right)}{x-x_0}=\phi \text{'}\left(x_0\right)=f\left(x_0\right)$

On a aussi :

$\underset{h\to 0}{\lim }\frac{1}{h}{\int }_{x_0}^{x_0+h}f\left(t\right)dt=f\left(x_0\right)$

2- Puisque $\ln$ est la primitive de la fonction $x\mapsto \frac{1}{x}$ sur ${\mathrm{ℝ}}_{+}^{*}$ qui s'annule en $1$ alors : $\left(\forall x\in {\mathrm{ℝ}}_{+}^{*}\right) \ln x={\int }_1^x\frac{1}{t}dt$

I- Intégrale d'une fonction continue sur un segment

1-2/ Expression d'une primitive à l'aide d'une intégrale

Proposition 2

Soit $f$ une fonction continue sur un intervalle $I$ et $v$ une fonction dérivable sur un intervalle $J$ telle que $v\left(J\right)\subset I$. Alors pour tout $a\in I$  :

La fonction $F:x\mapsto {\int }_a^{v\left(x\right)}f\left(t\right)dt$ est dérivable sur $J$ et de plus :

$\left(\forall x\in J\right) F\text{'}\left(x\right)=v\text{'}\left(x\right)f\left(v\left(x\right)\right)$

I- Intégrale d'une fonction continue sur un segment

1-2/ Expression d'une primitive à l'aide d'une intégrale

Applications

Montrer que les fonctions $F$ et $G$ définies par $F\left(x\right)={\int }_{\sin x}^{\cos x}\sqrt{1-t^2}dt$ et $G\left(x\right)={\int }_{-x}^{2x}\ln \left(e^t+1\right)dt$ sont dérivables sur $\mathrm{ℝ}$ et déterminer leurs fonctions dérivées.

I- Intégrale d'une fonction continue sur un segment

1-3/ Interprétation géométrique d'une intégrale

Proposition 3

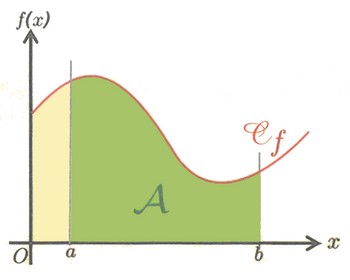
Soit $f$ une fonction continue et positive sur un segment $\left[a;b\right] \left(a<b\right)$ et ${\mathcal{C}}_f$ sa courbe représentative dans un repère orthogonal.

L'aire du domaine délimité par la courbe ${\mathcal{C}}_f$, l'axe des abscisses et les droites d'équations $x=a$ et $x=b$ est $\mathcal{A}={\int }_a^{b}f\left(x\right)dx$ (exprimée en unités d’aire)

I- Intégrale d'une fonction continue sur un segment

1-3/ Interprétation géométrique d'une intégrale

Applications

Soit $f$ la fonction numérique définie sur $\mathrm{ℝ}$ par $f\left(x\right)=6+5e^x-e^{2x}$, et ${\mathcal{C}}_f$ sa courbe représentative dans un repère orthonormé $\left(O,\overrightarrow{i},\overrightarrow{j}\right)$ avec $||\overrightarrow{i}||=||\overrightarrow{j}||=2cm$.

      Résoudre dans $\mathrm{ℝ}$ l'inéquation $f\left(x\right)\ge 0$, puis déterminer l'aire du domaine délimité par ${\mathcal{C}}_f$, les axes du repère et la droite d'équation $x=\ln \left(\frac{5}{2}\right)$.

II- Techniques de calcul d’intégrales

2-1/ Utilisation des primitives

Pour calculer une intégrale, on envisage en premier temps d'utiliser le tableau des primitives des fonctions usuelles et leurs propriétés.

Ainsi, et avant d'entamer le calcul d'une intégrale d'une fonction $f$, on doit vérifier la continuité de $f$ sur l'intervalle d'intégration, puis voir si $f$ s'écrit sous la forme $u\text{'}.\left(v\text{'}\circ u\right)$ (car une primitive de $f$ est donc $v\circ u$), ou bien voir si le problème demande de transformer l'expression de la fonction $f$ en une somme des fonctions faciles à intégrer.

Maintenant que le lien entre recherche de primitives et calcul d'intégrales a été rappelé, nous allons donner deux méthodes permettant de simplifier le calcul d'intégrales et donc la recherche des primitives, à savoir :

• Intégration par parties
• Intégration par changement de variable

II- Techniques de calcul d’intégrales

2-2/ Intégration par parties

Proposition 4

Soit $u$ et $v$ deux fonctions dérivables sur un intervalle $I$ telles que ses dérivées $u\text{'}$ et $v\text{'}$ soient continues sur $I$.

Alors pour tout $\left(a;b\right)\in I^2$ on a :

${\int }_a^{b}u\text{'}\left(t\right)v\left(t\right)dt={\left[u\left(t\right)v\left(t\right)\right]}_a^b-{\int }_a^{b}u\left(t\right)v\text{'}\left(t\right)dt$

II- Techniques de calcul d’intégrales

2-2/ Intégration par parties

Applications

En appliquant la formule d'intégration par parties, calculer les intégrales suivantes :

$$\begin{gathered} I_1={\int }_1^{\ln 2}x{e}^{x}dx \\ {I}_2={\int }_1^{2}x\sqrt{2-x}dx \\ {I}_3={\int }_0^{\sqrt{3}}\ln \left(t^2+1\right)dx \end{gathered}$$

II- Techniques de calcul d’intégrales

2-3/ Intégration par changement de variable

Proposition 5

Soit $f$ une fonction continue sur un intervalle $I$.

Soit $u$ une fonction dérivable sur un intervalle $E$ telle que $u\text{'}$ est continue sur $E$ et $u\left(E\right)\subset I$.

On a alors pour tout $\left(\alpha ,\beta \right)\in E^2$ :

${\int }_{\alpha }^{\beta }f\left(u\left(t\right)\right).u\text{'}\left(t\right)dt={\int }_{u\left(\alpha \right)}^{u\left(\beta \right)}f\left(x\right)dx$

Si $u$ est une bijection de $E$ vers $I$, alors pour tout $\left(a;b\right)\in I^2$ on a :

${\int }_a^{b}f\left(x\right)dx={\int }_{u^{-1}\left(a\right)}^{u^{-1}\left(b\right)}f\left(u\left(t\right)\right).u\text{'}\left(t\right)dt$

II- Techniques de calcul d’intégrales

2-3/ Intégration par changement de variable

Remarque

Pratiquement et en posant $x=u\left(t\right)$, on trouve $\frac{dx}{dt}=u\text{'}\left(t\right)$, c’est-à-dire que $dx=u\text{'}\left(t\right)dt$, de sorte que l'expression $f\left(u\left(t\right)\right).u\text{'}\left(t\right)dt$ soit égale à l'expression $f\left(x\right)dx$, et on a :

$t=\alpha \Rightarrow x=u\left(\alpha \right)$ et $t=\beta \Rightarrow x=u\left(\beta \right)$

On dit qu’on a effectué un changement de variable en posant $x=u\left(t\right)$.

II- Techniques de calcul d’intégrales

2-3/ Intégration par changement de variable

Applications

Calculer les intégrales suivantes :

$$\begin{gathered} I_1={\int }_0^1\sqrt{\frac{1-x}{1+x}}dx (poser x=\cos t) \\ {I}_2={\int }_0^3\frac{1}{1+\sqrt{1+x}}dx (poser t=1+\sqrt{1+x}) \end{gathered}$$