
Mathématiques : 1Bac S.Exp – STE – STM – Eco
Séance 1 (Notions de logique)
Professeur : Mr ETTOUHAMY Abdelhak
Sommaire
I- Définitions
1-1/ Proposition
1-2/ Fonction propositionnelle
1-3/ Quantificateurs
II- Opérations sur les propositions
2-1/ La négation d’une proposition
2-2/ La conjonction de deux propositions – La disjonction de deux propositions
2-3/ L’implication de deux propositions
2-4/ L’équivalence de deux propositions
2-5/ Les lois logiques
III- Types de raisonnements
3-1/ Raisonnement par contre exemple
3-2/ Raisonnement par des équivalences successives
3-3/ Raisonnement déductif
3-4/ Raisonnement par la contraposée
3-5/ Raisonnement par la disjonction des cas
3-6/ Raisonnement par l'absurde
3-7/ Raisonnement par la récurrence
V- Exercices
5-1/ Exercice 1
5-2/ Exercice 2
5-3/ Exercice 3
5-4/ Exercice 4
5-5/ Exercice 5
5-6/ Exercice 6
5-7/ Exercice 7
I- Définitions
1-1/ Proposition
tout énoncé mathématique (texte mathématique) qui a un sens pouvant être vrai ou faux (mais pas les deux en même temps) est une proposition.
On note souvent une proposition par les lettres P, Q ou R ..etc...
Exemple
I- Définitions
1-2/ Fonction propositionnelle
On appelle une fonction propositionnelle, tout énoncé mathématique contenant une variable x ou plusieurs variables (x,y, z,...), et qui appartiennent à des ensembles déterminés.
On note P(x) ou P(x,y;z,...).
Exemple
I- Définitions
1-3/ Quantificateurs
Quantificateur universel
L’expression suivante « pour tout x de E la proposition Q(x) est vraie », on la note : .
Le symbole s’appelle quantificateur universel et il se lit :
- pour tout
- quel que soit
Exemple :
I- Définitions
1-3/ Quantificateurs
Quantificateur existentiel
L’expression suivante « il existe un x de E tel que la proposition Q(x) est vraie », on la note : .
Le symbole s’appelle quantificateur existentiel et il se lit :
- il existe
Exemple :
I- Définitions
1-3/ Quantificateurs
Symbole
L’expression suivante « il existe un unique x de E tel que la proposition Q(x) est vraie », on la note : .
Exemple :
I- Définitions
1-3/ Quantificateurs
Remarques
- L’ordre des quantificateurs de même type (universel ou bien existentiel) ne change pas le sens de la fonction propositionnelle.
- L’ordre des quantificateurs de types différents (universel et existentiel) change le sens de la fonction propositionnelle.
- La négation du quantificateur est le quantificateur .
- La négation du quantificateur est le quantificateur .
- Les écritures suivantes sont équivalentes :
- Les écritures suivantes sont équivalentes :
II- Opérations sur les propositions
2-1/ La négation d’une proposition
La négation d’une proposition est la proposition qu’on note ou non P tel que les valeurs de vérité de P et sont opposées.

II- Opérations sur les propositions
2-2/ La conjonction de deux propositions – La disjonction de deux propositions
La conjonction de deux propositions
La conjonction de deux propositions et est la proposition notée ou bien .
Elle est vraie seulement dans le cas où et sont toutes les deux vraies.

II- Opérations sur les propositions
2-2/ La conjonction de deux propositions – La disjonction de deux propositions
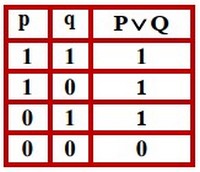
La disjonction de deux propositions
La disjonction de deux propositions et est la proposition notée ou bien .
Elle est fausse seulement dans le cas où et sont toutes les deux fausses.
II- Opérations sur les propositions
2-2/ La conjonction de deux propositions – La disjonction de deux propositions
Propriétés
La conjonction et la disjonction sont commutatives :
La conjonction et la disjonction sont associatives :
La négation de la conjonction :
La négation de la disjonction :
La conjonction est distributive sur la disjonction :
La disjonction est distributive sur la conjonction :
II- Opérations sur les propositions
2-3/ L’implication de deux propositions
Définition
L’implication de deux propositions puis est la proposition ; qu’on note par .
On lit implique Q.
La proposition s’appelle les données (ou hypothèses) de l’implication.
La proposition s’appelle la conclusion de l’implication.

II- Opérations sur les propositions
2-3/ L’implication de deux propositions
Propriétés
L’implication est transitive :
La négation de l’implication :
La contraposée :
II- Opérations sur les propositions
2-4/ L’équivalence de deux propositions
Définition
L’équivalence de deux propositions et est la proposition ; qu’on note par .
On lit est équivalente à ou bien si et seulement si .

II- Opérations sur les propositions
2-4/ L’équivalence de deux propositions
Propriétés
L’équivalence est transitive :
II- Opérations sur les propositions
2-5/ Les lois logiques
Définition
Une loi logique est une proposition qui est vraie quel que soit la vérité des propositions qui la constitue.
III- Types de raisonnements
3-1/ Raisonnement par contre exemple
Pour prouver que la propriétés suivante est fausse , il suffit de prouver que est vraie (c.à.d. de trouver un élément x de E qui ne vérifie pas P(x), c'est ce qu’on appelle un contre exemple).
Ce mode de raisonnement s’appelle raisonnement par contre exemple.
Exemple
III- Types de raisonnements
3-2/ Raisonnement par des équivalences successives
Pour démontrer que l’équivalence suivant est vrai, on démontrer que : et et et ... et .
Ce mode de raisonnement s’appelle raisonnement par des équivalences successives.
Exemple
III- Types de raisonnements
3-3/ Raisonnement déductif
Si on a l’implication est vraie et on a dans un exercice comme donnée la proposition donc on déduit que la proposition est vraie.
Ce mode de raisonnement s’appelle raisonnement par déduction.
Exemple
III- Types de raisonnements
3-4/ Raisonnement par la contraposée
Pour démontrer l’implication suivante , il suffit de démontrer l’implication suivante .
Ce mode de raisonnement s’appelle raisonnement par la contraposée.
Exemple
III- Types de raisonnements
3-5/ Raisonnement par la disjonction des cas
Lorsqu’on utilise plusieurs cas dans une démonstration, le raisonnement utilisé s’appelle raisonnement par disjonction des cas.
Exemple
III- Types de raisonnements
3-6/ Raisonnement par l'absurde
Pour démontrer qu’une proposition (conclusion ou résultat), et on a parmi les données la proposition .
On suppose que et au cour de la démonstration on trouve une contradiction
Ce mode de raisonnement s’appelle raisonnement par l'absurde.
Exemple
III- Types de raisonnements
3-7/ Raisonnement par la récurrence
Soient et une relation portant sur les entiers naturels tel que .
Pour démontrer que la relation est vraie pour tout , on utilise les étapes suivantes :
- On vérifie que est vraie pour (c.à.d. est vraie).
- On suppose que est vraie pour avec , la supposition s’appelle hypothèse de récurrence
- On démontre que la relation est vraie pour ( c.à.d. est vraie )
Ce mode de raisonnement s’appelle raisonnement par récurrence.
Exemple
V- Exercices
5-1/ Exercice 1
- Déterminer la valeur de vérité des propositions suivantes puis déterminer leurs négations :
V- Exercices
5-2/ Exercice 2
- Écrire les propositions suivantes en utilisant les quantificateurs :
"Pour tout entier naturel il existe un entier naturel tel que "
"Il existe un réel tel que pour tout , on a "
"Tout réel inférieur ou égal à est négatif"
"Il n’existe aucun nombre rationnel solution de l’équation "
"La fonction est constante sur "
"Tout entier naturel est pair ou impair"
"L’équation a une et une seule solution dans "
"Pour tout réel , il existe un unique entier relatif tel que "
"Il existe au moins un élément réel tel que pour tout , on a "
V- Exercices
5-3/ Exercice 3
- Déterminer la valeur de vérité des propositions suivantes puis déterminer leurs négations :
V- Exercices
5-4/ Exercice 4
Soit la proposition suivante :
- Donner la négation de la proposition .
- En déduire que est fausse.
Soit la proposition suivante : .
- Déterminer la vérité de la proposition .
- Donner la négation de .
V- Exercices
5-5/ Exercice 5
Raisonnement par le contre-exemple
- Montrer que la proposition suivante est fausse : "".
- Montrer que la proposition suivante est fausse : " est pair".
- Montrer que la proposition suivante est fausse : " est un entier premier".
Raisonnement par l’absurde
- Montrer que .
- Montrer que .
- Montrer que .
- Montrer que .
V- Exercices
5-6/ Exercice 6
Raisonnement par les équivalences
- Soient et deux réels. Montrer que .
- Montrer que ∀ x ∈ ℝ * :
Raisonnement par la disjonction des cas
- Résoudre dans l’équation suivante : .
- Montrer que ∀ n ∈ ℕ : est un nombre pair.
V- Exercices
5-7/ Exercice 7
Raisonnement par la contraposée
- Soient . Montrer que .
- Soient . Montrer que .
- Soient . Montrer que .
Raisonnement par la récurrence
- Montrer que est divisible par .
- Montrer que .


