Séance 4-1-1 : Fonctions logarithmiques - Partie 1 (Cours)

Sommaire

I- Fonction logarithme népérien

1-1/ Définition de la fonction ln

1-2/ Monotonie de la fonction ln

1-3/ Propriétés algébriques

1-4/ Limites usuelles

1-5/ Tableau de variations de la fonction ln

1-6/ Courbe de la fonction ln

1-7/ Limites fondamentales

1-8/ Dérivée logarithmique

I- Fonction logarithme népérien

1-1/ Définition de la fonction ln

Définition 1

La primitive de la fonction $x\mapsto \frac{1}{x}$ sur $]0;+\infty [$ et qui s'annule en $1$ est appelée la fonction logarithme népérienne.

On la note $\ln$.

Remarques

Le domaine de définition de la fonction $\ln$ est $]0;+\infty [$, et $\ln \left(1\right)=0$.

La fonction $\ln$ est dérivable sur $]0;+\infty [$ et de plus :

$\left(\forall x\in ]0;+\infty [\right) \ln \text{'}\left(x\right)=\frac{1}{x}$

On rappelle que toute fonction continue sur un intervalle admet une primitive d éfinie sur cet intervalle.

I- Fonction logarithme népérien

1-1/ Définition de la fonction ln

Applications

Déterminer le domaine de définition de chacune des fonctions suivantes :

$$\begin{gathered} f\left(x\right)=\ln \left(x+4\right)-\ln \left(25-x^2\right) \\ g\left(x\right)=\ln \left(x^2-8x+7\right) \end{gathered}$$

I- Fonction logarithme népérien

1-2/ Monotonie de la fonction ln

Proposition 1

La fonction ln est strictement croissante sur $]0;+\infty [$.

On a alors :

Pour tout $\left(x,y\right)\in {\left(]0;+\infty [\right)}^2$ :

$\ln x<\ln y\iff x<y$ et $\ln x=\ln y\iff x=y$

Pour tout $x\in ]0;+\infty [$ :

$\ln x=0\iff x=1$ et $\ln x>0\iff x>1$ et $\ln x<0\iff x<1$

I- Fonction logarithme népérien

1-2/ Monotonie de la fonction ln

Applications

1. Résoudre dans $\mathrm{ℝ}$ les équations et les inéquations suivantes :

$$\begin{gathered} \overline{)1} \ln \left(2x-3\right)=\ln \left(4-x\right) \\ \overline{)2} \ln \left(x^2+x\right)=\ln \left(-2x-2\right) \\ \overline{)3} \ln \left(3x^2+4x+2\right)=0 \\ \overline{)4} \ln \left(4x-5\right)>\ln \left(2x+3\right) \end{gathered}$$

I- Fonction logarithme népérien

1-3/ Propriétés algébriques

Proposition 2

Pour deux réels strictement positifs $x$ et $y$ on a : $\ln \left(xy\right)=\ln x+\ln y$ (Propriété fondamentale)

De cette propriété fondamentale on peut déduire les propriétés algébriques de la Proposition 3.

I- Fonction logarithme népérien

1-3/ Propriétés algébriques

Proposition 3

1- Pour tout réel strictement positif $x$, on a : $\ln \left(\frac{1}{x}\right)=-\ln x$

2- Pour tout $\left(x,y\right)\in {\left(]0;+\infty [\right)}^2$, on a : $\ln \left(\frac{x}{y}\right)=\ln x-\ln y$

3- Pour tout $n\in \mathrm{\mathbb{N}}*$, et pour tous réels strictement positifs $x_1,x_2,....,x_n$, on a :

$\ln \left(x_1{x}_2,....x_n\right)=\ln \left(x_1\right)+\ln \left(x_2\right)+...+\ln \left(x_n\right)$

C'est-à-dire : 

$\ln \left(\prod _{k=1}^n{x}_k\right)=\sum _{k=1}^n\ln \left(x_k\right)$

4- Pour tout $x\in ]0;+\infty [$, et pour tout $r\in \mathrm{\mathbb{Q}}$, on a : $\ln \left(x^r\right)=r\ln x$

I- Fonction logarithme népérien

1-3/ Propriétés algébriques

Remarques

1- Soit $a$ et $b$ deux réels strictement négatifs.

On a alors $ab>0$ et $\frac{a}{b}>0$.

11 s'ensuit donc : $\ln \left(ab\right)=\ln \left|a\right|+\ln \left|b\right|$ et $\ln \left(\frac{a}{b}\right)=\ln \left|a\right|-\ln \left|b\right|$

2- On a pour tout $x\in ]0;+\infty [$ et pour tout entier $n\ge 2$ : 

$\ln \left(\sqrt{x}\right)=\frac{1}{2}\ln x$ et $\ln \left(\sqrt[n]{x}\right)=\frac{1}{n}\ln x$

I- Fonction logarithme népérien

1-4/ Limites usuelles

Proposition 4

$$\begin{gathered} \underset{x\to +\infty }{\lim }\ln \left(x\right)=+\infty \\ \underset{x\to 0^{+}}{\lim }\ln \left(x\right)=-\infty \end{gathered}$$

I- Fonction logarithme népérien

1-5/ Tableau de variations de la fonction ln

Proposition 5

La fonction ln est une bijection de l'intervalle $]0;+\infty [$ vers $\mathrm{ℝ}$.

L'équation $\ln \left(x\right)=1$ admet une unique solution dans $]0;+\infty [$. On la note $e$ :

$\ln \left(x\right)=1\iff x=e$

Remarques

À l’aide de la calculatrice, on trouve comme valeur approchée de e : 2,718281828

On a pour tout $r\in \mathrm{\mathbb{Q}}$ : $ln\left(e^r\right)=r$

I- Fonction logarithme népérien

1-6/ Courbe de la fonction ln

Proposition 6

Soit $\mathcal{C}$ la courbe représentative de la fonction ln dans un repère orthonormé. Alors :

La courbe $\mathcal{C}$ admet l'axe des ordonnées comme asymptote.

La courbe $\mathcal{C}$ admet une branche parabolique de direction l'axe des abscisses : $\underset{x\to +\infty }{\lim }\frac{\ln x}{x}=0$

La courbe $\mathcal{C}$ est concave sur $]0;+\infty [$.

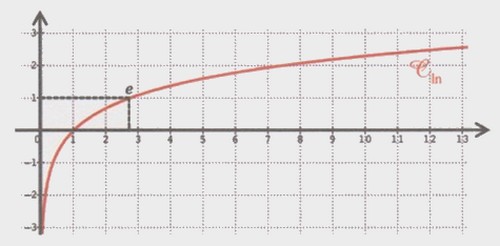
I- Fonction logarithme népérien

1-7/ Limites fondamentales

Proposition 7

On a :

$\underset{x\to 0^{+}}{\lim }x\ln x=0 ; \underset{x\to 1}{\lim }\frac{\ln x}{x-1}=1 ; \underset{x\to 0}{\lim }\frac{\ln \left(1+x\right)}{x}=1$

On a pour tout $r\in {\mathrm{\mathbb{Q}}}_{+}^{*}$ :

$\underset{x\to +\infty }{\lim }\frac{\ln x}{x^r}=0 ; \underset{x\to 0^{+}}{\lim }{x}^r\ln x=0$

I- Fonction logarithme népérien

1-7/ Limites fondamentales

Applications

Calculer les limites suivantes :

I- Fonction logarithme népérien

1-8/ Dérivée logarithmique

Proposition 8

Soit $u$ une fonction dérivable sur un intervalle $I$ de $\mathrm{ℝ}$ telle que $\left(\forall x\in I\right) , u\left(x\right)\ne 0$.

Alors la fonction $x\mapsto \ln \left|u\left(x\right)\right|$ est dérivable sur $I$, et on a : $\left(\ln \left|u\left(x\right)\right|\right)\text{'}=\frac{u\text{'}\left(x\right)}{u\left(x\right)}$

I- Fonction logarithme népérien

1-8/ Dérivée logarithmique

Applications

Déterminer les dérivées des fonctions suivantes :

$$\begin{gathered} \overline{)1} f\left(x\right)=\ln \left|\ln x\right| \\ \overline{)2} g\left(x\right)=x.\sqrt[3]{\ln x-2} \\ \overline{)3} h\left(x\right)=\ln \left|\cos x\right| \\ \overline{)4} k\left(x\right)=\ln \left(\frac{1}{2-\ln x}\right) \end{gathered}$$

I- Fonction logarithme népérien

1-8/ Dérivée logarithmique

Définition 2

Soit $u$ une fonction dérivable sur un intervalle $I$ telle que $\left(\forall x\in I\right) , u\left(x\right)\ne 0$.

La fonction $\frac{u\text{'}}{u}$ est appelée la dérivée logarithmique de la fonction $u$ sur l'intervalle $I$.

I- Fonction logarithme népérien

1-8/ Dérivée logarithmique

Proposition 9

Soit $u$ une fonction dérivable sur un intervalle $I$ telle que $\left(\forall x\in I\right) , u\left(x\right)\ne 0$.

Les primitives de la fonction $x\mapsto \frac{u\text{'}\left(x\right)}{u\left(x\right)}$ sur $I$ sont les fonctions $x\mapsto \ln \left|u\left(x\right)\right|+\lambda$ avec $\lambda \in \mathrm{ℝ}$.

I- Fonction logarithme népérien

1-8/ Dérivée logarithmique

Applications

       Dans chacun des cas suivants, déterminer les primitives de la fonction $f$ sur l’intervalle $I$ :

$$\begin{gathered} \overline{)1} f\left(x\right)=\frac{\sin \left(2x\right)}{5+{\sin }^{2}x} ; I=\mathrm{ℝ} \\ \overline{)2} f\left(x\right)=\frac{x-3}{x^2-6x} ; I={\mathrm{ℝ}}_{-}^{*} \\ \overline{)3} f\left(x\right)=\frac{\ln x}{x\left({\ln }^2\left(x\right)-1\right)} ; I=]e;+\infty [ \\ \overline{)4} f\left(x\right)=\frac{5x+7}{2x-4} ; I=]2;+\infty [ \end{gathered}$$​