Séance 18 - Prisme droit, pyramide et cône de révolution

Sommaire

I- Prisme droit (Rappel)

1-1/ Définition

1-2/ Remarques

1-3/ Aire littérale - Aire totale - Volume

1-4/ Patron d’un prisme

II- Pyramide

2-1/ Définition

2-2/ Pyramide régulière

2-3/ Patron d’une pyramide

2-4/ Aire latérale et aire totale d'une pyramide

2-5/ Volume d'une pyramide

III- Cône de révolution

3-1/ Définition

3-2/ Patron d'un cône de révolution

3-3/ Aire latérale et aire totale d'un cône de révolution

3-4/ Volume d'un cône de révolution

IV- Exercices

4-1/ Exercice 1

4-2/ Exercice 2

4-3/ Exercice 3

4-4/ Exercice 4

4-5/ Exercice 5

4-6/ Exercice 6

4-7/ Exercice 7

I- Prisme droit (Rappel)

1-1/ Définition

Le prisme droit est un Solide possède :

• Deux polygones Superposables et parallèles Sont deux baSeS du prisme.
• Des rectangles pour autres faces sont les faces latérales du prisme.

Exemple

I- Prisme droit (Rappel)

1-2/ Remarques

1. Lorsque la base est un rectangle (prisme de base quadrilatère), le prisme droit obtenu est un parallélépipède rectangle :

2. Lorsque la base est un carré (prisme de base quadrilatère), le prisme droit obtenu est un cube :

3. Lorsque la base du prisme est un triangle ; On dit que ce prisme est un prisme de base triangulaire :

4. Le nombre des faces latérales d’un solide est égale le nombre des côtes de sa base.

I- Prisme droit (Rappel)

1-3/ Aire littérale - Aire totale - Volume

Pour calculer l'aire latérale $A_L$ d'un prisme droit, on multiplie le périmètre $p$ d’une base par la hauteur $h$ du solide :

$\overline{) A_L=p\times h }$

L'aire totale $A_T$ d'un prisme droit est égale à la somme de $A_L$ (son aire latérale) et les deux aires de ses deux bases :

$\overline{) A_T=A_L+2A_B }$

Pour calculer le volume $V$ d'un prisme droit, on multiplie $A_B$ l'aire d'une base par la hauteur $h$ du solide :

$\overline{) V=A_B\times h }$

Exemple

I- Prisme droit (Rappel)

1-4/ Patron d’un prisme

Patron d'un prisme dont la base est un triangle

Patron d'un prisme dont la base est un rectangle (Pavé droit (parallélépipède rectangle))

Patron d'un prisme dont la base est un carré (un cube)

II- Pyramide

2-1/ Définition

Une pyramide est un solide ayant :

• Une face polygonale appelée base.
• Toutes les autres faces sont des triangles qui ont un sommet commun appelé sommet de la pyramide, ces faces triangulaires sont appelées faces latérales.

Si la base est aussi triangulaire, alors cette pyramide est appelée tétraèdre :

II- Pyramide

2-2/ Pyramide régulière

Définition

Une pyramide de sommet $S$ est dite régulière lorsque :

• Sa base est un polygone régulier de centre $O$ (triangle équilatéral, carré, ...)
• $\left[SO\right]$ est la hauteur de la pyramide.

Exemples

Pyramide régulière à base triangulaire ($ABC$ est un triangle équilatéral de centre de gravité $O$) :

Pyramide régulière à base carrée ($ABCD$ est un carré de centre $O$) :

II- Pyramide

2-3/ Patron d’une pyramide

Un patron d’un solide est un dessin en grandeur réelle qui permet de fabriquer le solide après le découpage et pliage :

II- Pyramide

2-4/ Aire latérale et aire totale d'une pyramide

L'aire latérale $A_L$ d'une pyramide est égale à la somme des aires de ses faces latérales.

L'aire totale $A_T$ d' une pyramide est égale à la somme de son aire latérale AL et l’aire de sa base : $A_T=A_L+A_B$

II- Pyramide

2-5/ Volume d'une pyramide

Le volume $V$ d'une pyramide est égal au tiers du produit de sa hauteur $h$ par $A_B$ l’aire de sa base :

$\overline{) V=\frac{1}{3}\times A_B\times h }$

Exemple

L'aire de la base d'une pyramide est égale à $123c{m}^2$, et sa hauteur est égale à $8cm$.

• Calculons $V$ son volume.

III- Cône de révolution

3-1/ Définition

Un cône de révolution est un solide obtenu par rotation d'un triangle rectangle autour d'un axe correspondant à l'un des côtés formant l'angle droit.

Il est constitué d'une base qui correspond à un disque et d'une surface latérale conique.

Le cône possède, une hauteur qui correspond à la droite perpendiculaire à sa base et passant par son sommet.

III- Cône de révolution

3-2/ Patron d'un cône de révolution

III- Cône de révolution

3-3/ Aire latérale et aire totale d'un cône de révolution

L'aire latérale $A_L$ d'un cône de révolution de rayon $R$ et de génératrice $a$ est :

$\overline{) A_L=\mathrm{\pi }\times R\times a }$

L'aire totale $A_T$ d'un cône de révolution est égale à la somme de $A_L$ son aire latérale et l'aire de sa base :

$\overline{) A_T=A_L+A_B }$

Exemple

• Calculons l’aire latérale d’un cône de révolution tel que : $R=2cm$ et $a=5cm$

III- Cône de révolution

3-4/ Volume d'un cône de révolution

Le volume $V$ d'un cône de révolution est égal au tiers du produit de sa hauteur $h$ par $A_B$ l’aire de sa base :

$\overline{) V=\frac{1}{3}\times A_B\times h }$

Exemple

IV- Exercices

4-1/ Exercice 1

1. Associer chaque solide à son patron :

IV- Exercices

4-2/ Exercice 2

Ces solides ont la même hauteur 4cm :

1. Calculer l’aire de chaque base.

2. Calculer le volume de chaque solide.

3. Quel est celui qui est le plus volumineux ?

IV- Exercices

4-3/ Exercice 3

1. Construire le patron du prisme droit suivant :

IV- Exercices

4-4/ Exercice 4

$SEFGH$ est une pyramide à base rectangulaire :

1. Calculer la longueur $EG$.

2. Calculer la longueur $SO$.

Voici un cône de révolution :

3. Calculer la longueur $SM$.

IV- Exercices

4-5/ Exercice 5

Voici un patron de cône de révolution :

1. Quel est le sommet de ce cône ?

2. Quel est le centre et le rayon de son disque de base ?

3. Quelle est la longueur d’une génératrice ?

4. Calculer la longueur de l’arc de cercle $BC$.

5. Calculer l’angle $\widehat{BAC}$.

IV- Exercices

4-6/ Exercice 6

On considère le patron d'un cône de révolution dont la base a pour rayon $3cm$ et la surface latérale qui a pour rayon $5cm$ :

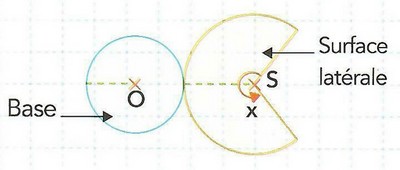
1. Montrer que le périmètre du disque de la base est égal à $6\mathrm{\pi }$.

2. Montrer que le périmètre de l'arc du cercle de centre $S$ est égal à $10\mathrm{\pi }$.

On considère le tableau de proportionnalité suivant :

3. Trouver la valeur de $x$.

4. Calculer le volume du cône.

IV- Exercices

4-7/ Exercice 7

$ABCDEFGH$ est un parallélépipède rectangle tels que $AB=4,5cm$, $BC=3cm$ et $AE=2,5cm$ :

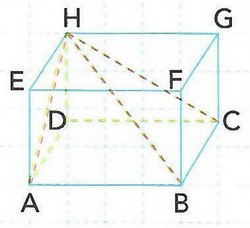
1. Calculer les distances $BE$ et $AC$.

2. Calculer le volume de $ABCDEFGH$.

On considère la pyramide $ABCDH$ de base $ABCD$ et de sommet $H$.

3. Quelle est la nature de chacun des triangles $ADH$ et $DHC$ ?

4. Calculer le volume de $ABCDH$.