
Mathématiques : 3ème Année Collège
Séance 17 (Statistiques)
Professeur : Mr BENGHANI Youssef
Sommaire
I- Rappel
II- Tableau des effectifs, des effectifs cumulés, des fréquences et des fréquences cumulées
2-1/ Exemple 1 : Série statistique en valeurs
2-2/ Exemple2 : Série statistique en classes
III- Moyenne arithmétique (ou moyenne pondérée)
3-1/ Définition
3-2/ Exemple 1 : Série statistique en valeurs
3-3/ Exemple 2 : Série statistique en classes
IV- Médiane d'une série statistique
4-1/ Définition
4-2/ Exemple 1 : L’effectif total est un nombre impair
4-3/ Exemple 2 : L’effectif total est un nombre pair
4-4/ Applications
V- Mode d'une série statistique
5-1/ Définition
5-2/ Exemple 1
5-3/ Exemple 2
VI- La dispersion
6-1/ Définition
6-2/ Exemple
VII- Exercices
7-1/ Exercice 1
7-2/ Exercice 2
7-3/ Exercice 3
7-4/ Exercice 4
7-5/ Exercice 5
7-6/ Exercice 6
I- Rappel
Population
On appelle population un ensemble de personnes ou d’objets étudiés.
Un individu est un élément de la population.
Caractère ou variable
La particularité de la population étudiée en statistique est appelée caractère ou variable.
Le caractère étudié peut être :
- Quantitatif discret quand il prend un nombre fini de valeurs numériques.
- Quantitatif continu quand il prend une infinité de valeurs numériques. Les valeurs sont alors regroupées dans des intervalles appelés classes.
- Qualitatif quand il ne prend pas que des valeurs numériques.
Effectif
On appelle effectif d’une valeur (ou classe) du caractère le nombre de fois où cette valeur apparaît dans la série.
I- Rappel
Effectif cumulé
L’effectif cumulé d’une valeur est la somme de l’effectif de cette valeur avec les précédentes.
Fréquence
La fréquence d'une valeur est le quotient de l'effectif de la valeur par l'effectif total.
Fréquence cumulée
La fréquence cumulée est le rapport de l'effectif cumulé correspond à cette valeur et l’effectif totale.
II- Tableau des effectifs, des effectifs cumulés, des fréquences et des fréquences cumulées
2-1/ Exemple 1 : Série statistique en valeurs
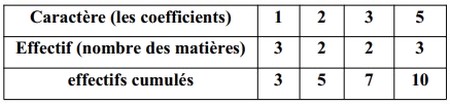
Le tableau suivant donne une classification des matières enseignées dans le troisième collège, selon ses coefficients :
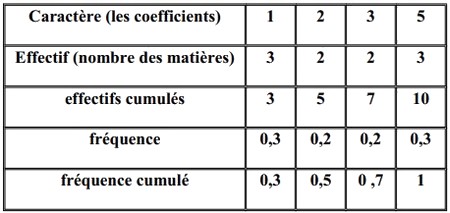
II- Tableau des effectifs, des effectifs cumulés, des fréquences et des fréquences cumulées
2-2/ Exemple 2 : Série statistique en classes
Le tableau suivant donne des résultats sur la taille des personnes classées en quatre catégories :
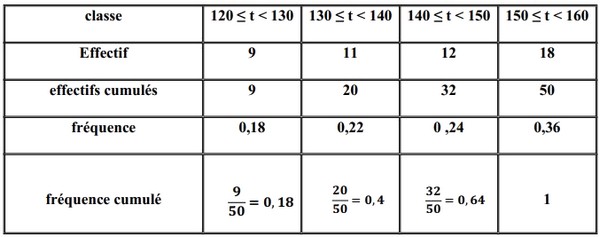
III- Moyenne arithmétique (ou moyenne pondérée)
3-1/ Définition
La moyenne d’une série statistique est égale au quotient de la somme de toutes les valeurs de cette série par l’effectif total.
On la note m.
III- Moyenne arithmétique (ou moyenne pondérée)
3-2/ Exemple 1 : Série statistique en valeurs
Calculons la moyenne arithmétique de la série statistique suivante :

III- Moyenne arithmétique (ou moyenne pondérée)
3-3/ Exemple 2 : Série statistique en classes
Le centre de classe a≤x≤b est le nombre a+b2
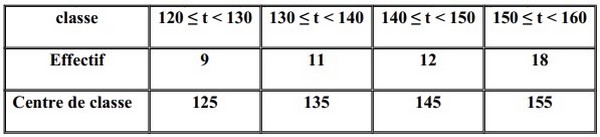
IV- Médiane d'une série statistique
4-1/ Définition
La médiane est la valeur centrale d'une série statistique dont les valeurs observées ont été rangées dans l'ordre croissant.
C'est la valeur qui partage la population étudiée en deux sous ensembles de même effectif (si le nombre d'observations n est pair, la médiane est la moyenne (demi-somme) des termes de rang n et n + 1 (exemple 2).
IV- Médiane d'une série statistique
4-2/ Exemple 1 : L’effectif total est un nombre impair
On considère la série statistique suivante triée par ordre croissant :
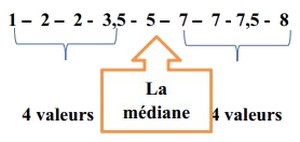
La médiane de cette série statistique est : 5
IV- Médiane d'une série statistique
4-3/ Exemple 2 : L’effectif total est un nombre pair
On considère la série statistique suivante triée par ordre croissant :

Tout nombre compris entre 5 et 7 est une médiane pour cette série statistique.
En général, on choisit le milieu. Alors la médiane de la série statistique est : 6
IV- Médiane d'une série statistique
4-4/ Applications
Application 1
Il a été demandé aux élèves du collège la durée de leur trajet pour se rendre au collège.
Les résultats sont consignés dans le tableau suivant :
Application 2
Calculons la médiane de la série statistique suivante :

V- Mode d'une série statistique
5-1/ Définition
Le mode d'une série statistique est la valeur du caractère qui a le plus grand effectif.
V- Mode d'une série statistique
5-2/ Exemple 1
On considère le tableau statistique suivant :

Déterminons la classe du mode de la série statistique.
V- Mode d'une série statistique
5-3/ Exemple 2
On considère le tableau statistique suivant :

Déterminons la classe du mode de la série statistique.
VI- La dispersion
6-1/ Définition
On considère deux séries statistiques S1 et S2 de même moyenne arithmétique M.
S1 est moins dispersée que S2 signifie que les valeurs du caractère de S1 sont près à la moyenne M que les valeurs de S2.
VI- La dispersion
6-2/ Exemple
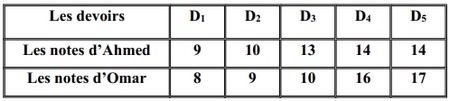
Dans le tableau suivant les notes de cinq devoirs de deux élèves Ahmed et Omar :
VII- Exercices
7-1/ Exercice 1
Voici les notes obtenues par des élèves à un devoir de mathématiques :
14 – 6 – 14 – 6 – 7 – 12 – 14 – 13 – 15 – 9 – 8 – 12
9 – 12 – 12 – 16 – 12 – 9 – 13 – 9 – 6 – 7 – 8 – 9 – 15 – 12
14 – 14 – 13 – 6 – 15 – 13 – 12 – 9 – 9 – 7 – 6 – 12 – 7 – 15
- Construire un tableau des effectifs et des effectifs cumulés et les fréquences et les fréquences cumulées.
- Déterminer la médiane de cette série.
- Déterminer le mode de cette série.
- Calculer la moyenne de cette série de notes.
- Représenter cette série par un diagramme en bâtons.
VII- Exercices
7-2/ Exercice 2
Le tableau suivant donne la répartition des notes d’une classe à un contrôle :

- Quel est l’électif total de cette série ?
- Recopier et compléter le tableau.
- Calculer la fréquence de 12, et en déduire le pourcentage des élèves qui ont obtenu une note égale à 12.
- Calculer la note moyenne de la classe, à ce contrôle.
- Déterminer la médiane de cette série.
- Déterminer le mode de cette série.
- Calculer le pourcentage des élèves qui ont obtenu une note supérieure ou égale à la note moyenne de la classe.
- Réaliser un diagramme en bâtons
VII- Exercices
7-3/ Exercice 3
Le tableau suivant donne les notes obtenues par 25 élevés au dernier devoir de contrôle continu :
- Recopier et compléter le tableau.
- Donner le tableau des effectifs, les effectifs cumulés, les fréquences et les fréquences cumulés.
- Déterminer le mode de cette série statistique.
- Déterminer la classe qui contient la médiane de cette série statistique (ou bien déterminer la médiane).
- Calculer la valeur moyenne de cette série statistique.
- Calculer le pourcentage de l’échantillon 4≤n<12.
- Réaliser l’histogramme de cette série statistique.
VII- Exercices
7-4/ Exercice 4
On donne ci-dessous la répartition des mosquées dans une ville du Maroc selon leur superficie en m2 :
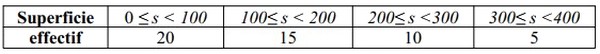
- Quel est le nombre de mosquées qui ont plus de 100m2.
- Calculer la fréquence cumulé associée à la classe 200≤s<300.
- Donner le pourcentage des mosquées qui ont une superficie inférieure à 200m2.
- Déterminer la classe modale.
- Déterminer la médiane.
- Calculer la superficie moyenne des mosquées.
VII- Exercices
7-5/ Exercice 5
Le tableau suivant, représente le résultat d'une étude sur la masse (en kg) des cartables 4 des élèves :
| Masse (en kg) | Effectif | Effectif cumulé croissant | Fréquence en % |
| 1≤m<3 | 10 | ||
| 3≤m<5 | 25 | ||
| 5≤m<7 | 30 | ||
| 7≤m<9 | 15 |
- Compléter le tableau.
- Déterminer la classe modale.
- Déterminer la classe contenant la médiane .
- Calculer la masse moyenne
- Tracer un histogramme représentant le tableau des effectifs.
VII- Exercices
7-6/ Exercice 6
L'histogramme suivant représente les pointures des chaussures des élèves d'un collège :

- Compléter le tableau suivant :
| Pointure | Effectif | Effectif cumulé croissant | Fréquence en % |
| 28≤p<30 | 12 | ||
| 30≤p<32 | |||
| 32≤p<34 | |||
| 34≤p<36 | |||
| 36≤p<38 |
- Déterminer la classe modale.
- Déterminer la classe de la médiane
- Calculer la moyenne.
- Tracer un diagramme circulaire.


