Maths 3AC - Examen Régional 3

I- Exercice 1

1. Résoudre les équations suivantes :

$$\begin{gathered} \overline{)1} 3x-5=7 \\ \overline{)2} \left(x+1\right)\left(x-\sqrt{3}\right)=0 \end{gathered}$$

2. Résoudre l’inéquation :

$5x+12<2$

3. Résoudre le système suivant :

$\left\{\begin{array}{l}3x+y=1\\ 5x-y=-9\end{array}\right.$

4. Problème

Ahmed a payé 130 DH pour l’achat de légumes et fruits ; le prix des achats de légumes dépasse celui des fruits de 20 DH.

• Détermine le prix payé pour l’achat des légumes et le prix payé pour l’achat des fruits.

II- Exercice 2

On considère la fonction linéaire $f$ tel que : $f\left(3\right)=-6$.

1. Vérifier que : $f(𝑥)=-2𝑥$.

2. Calculer $f\left(5\right)$.

3. Déterminer le nombre dont l’image est $2$ par la fonction $f$.

4. Tracer la représentation graphique de la fonction $f$ dans un repère orthonormé $\left(O,I,J\right)$.

III- Exercice 3

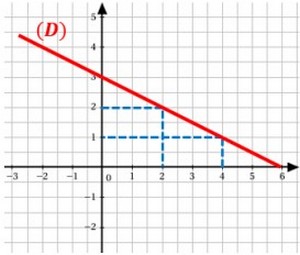
La droite $\left(D\right)$ représentée ci-dessous est la représentation graphique d’une fonction affine $g$.

1. Déterminer l’image de $2$ par la fonction $g$.

2. Déterminer le nombre dont l’image est $1$ par la fonction $g$.

3. Vérifier que : $g\left(4\right)-g\left(2\right)=-1$.

4. Montrer que le coefficient de la fonction $g$ est : $-\frac{1}{2}$.

5. Déterminer l’expression de la fonction $g$.

IV- Exercice 4

Dans le plan rapporté à un repère orthonormé $\left(O,I,J\right)$, on considère les points : $A(4,4)$, $B(1,5)$ et $C(3,1)$.

1. Représenter les points $A$, $B$ et $C$ dans le repère $\left(O,I,J\right)$.

2. Détermine les coordonnées du vecteur $\overrightarrow{AB}$.

3. Vérifier que : $AB=\sqrt{10}$.

4. Vérifier que le point $K(2,3)$ est le milieu du segment $\left[BC\right]$.

5. Vérifier que les points $B$ et $C$ appartiennent à la droite d’équation $y=-2x+7$.

Soit $\left(D\right)$ la droite parallèle à la droite $\left(BC\right)$ et qui passe par le point $A$.

6. Déterminer le coefficient directeur de la droite $\left(D\right)$.

7. En déduire l’équation réduite de la droite $\left(D\right)$.

Soit $\left(D\text{'}\right)$ la droite d’équation $y=\frac{1}{2}x+2$.

8. Montrer que les droites $\left(D\right)$ et $\left(D\text{'}\right)$ sont perpendiculaires.

V- Exercice 5

Soit $ABC$ un triangle et $I$ le milieu du segment $\left[BC\right]$.

$K$ est le symétrique de $A$ par rapport au point $I$.

On considère la translation $T$ qui transforme $A$ en $C$.

1. Tracer $J$ l’image de $I$ par la translation $T$.

2. Vérifier que le quadrilatère $ABKC$ est un parallélogramme.

3. En déduire l’image de $B$ par la translation $T$.

On suppose que $\widehat{AIB}=110°$.

4. Déterminer l’image de l’angle $\widehat{AIB}$ par la translation $T$.

5. En déduire la mesure de l’angle $\widehat{CJK}$.