Séance 24B - Oscillateurs mécaniques (Pendule pesant, simple et de torsion)

Sommaire

I- Pendule de torsion

1-1/ Moment du couple de torsion

1-2/ Équation différentielle du mouvement

1-3/ Équation horaire du mouvement

II- Pendule pesant

2-1/ Équation différentielle du mouvement

2-2/ Équation horaire du mouvement

III- Pendule simple

3-1/ Équation différentielle du mouvement

3-2/ Équation horaire du mouvement

IV- Oscillations forcées et résonance

4-1/ Définition

4-2/ Exemple d'oscillations forcées

4-3/ Phénomène de résonance

V- Exercices

5-1/ Exercice 1

5-2/ Exercice 2

5-3/ Exercice 3

I- Pendule de torsion

1-1/ Moment du couple de torsion

Le pendule de torsion est constitué d'un fil de torsion, et d'une tige homogène horizontale fixée en son milieu à l’extrémité de ce fil.

Lorsqu’on écarte la tige de sa position d'équilibre et on la libère, elle se met à osciller autour de sa position d'équilibre.

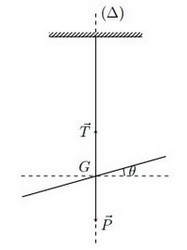L'action du fil tordu sur la tige est dû à un ensemble de forces auxquelles on associe un couple de forces appelé couple de torsion : ${\mathcal{M}}_t=-C.\theta$

• ${\mathcal{M}}_t$ : moment du couple de torsion (N.m)
• $C$ : Constante de torsion (N.m/rad)
• $\theta$ : angle de torsion (rad)

I- Pendule de torsion

1-2/ Équation différentielle du mouvement

On écarte la tige de sa position d'équilibre d'un angle ${\theta }_m$ et on la libère sans vitesse initiale :

Le bilan des forces : $\overrightarrow{P}$ : Le poids de la barre $\overrightarrow{T}$ : La tension du fil $C$ : Le couple de torsion

D’après la relation fondamentale de la dynamique on a :

$$\begin{gathered} \sum _{}^{}{\mathcal{M}}_{\left(\Delta \right)}\left(\overrightarrow{F}\right)=J_{\Delta }.\ddot{\theta } \\ {\mathcal{M}}_{\left(\Delta \right)}\left(\overrightarrow{P}\right)+{\mathcal{M}}_{\left(\Delta \right)}\left(\overrightarrow{T}\right)+{\mathcal{M}}_t=J_{\Delta }.\ddot{\theta } \\ {\mathcal{M}}_t=J_{\Delta }.\ddot{\theta } \\ -C.\theta ==J_{\Delta }.\ddot{\theta } \\ \overline{)\ddot{\theta }+\frac{C}{J_{\Delta }}\theta =0} \end{gathered}$$

I- Pendule de torsion

1-3/ Équation horaire du mouvement

L'équation du mouvement est : $\ddot{\theta }+\frac{C}{J_{\Delta }}\theta =0$

C’est une équation différentielle linéaire du seconde ordre, sa solution est :

$\theta ={\theta }_m\cos \left(\frac{2\mathrm{\pi }}{T_0}t+\phi \right)={\theta }_m\cos \left({\omega }_{0}t+\phi \right)$

Calcul de $T_0$

$$\begin{gathered} \theta ={\theta }_m\cos \left({\omega }_{0}t+\phi \right) \\ \Rightarrow \dot{\theta }=-{\theta }_m{\omega }_0\sin \left({\omega }_{0}t+\phi \right) \\ \Rightarrow \ddot{\theta }=-{\theta }_m{{\omega }_0}^2\cos \left({\omega }_{0}t+\phi \right)=-{{\omega }_0}^2.\theta \\ \Rightarrow {{\omega }_0}^2=\frac{C}{J_{\Delta }} \\ \Rightarrow {\omega }_0=\sqrt{\frac{C}{J_{\Delta }}}=\frac{2\mathrm{\pi }}{T_0} \\ \Rightarrow \overline{){\mathrm{T}}_0=2\mathrm{\pi }\sqrt{\frac{{\mathrm{J}}_{\mathrm{\Delta }}}{\mathrm{C}}}} \end{gathered}$$

II- Pendule pesant

2-1/ Équation différentielle du mouvement

Le pendule pesant, est tout solide mobile autour un axe $(∆)$, horizontal et fixe ne passant pas par son centre d’inertie.

On écarte le pendule pesant de sa position d'équilibre et on le libère sans vitesse initiale.

Appelons $\theta$ l'angle que forme OG avec la ligne verticale passant par O.

Le bilan des forces :

• $\overrightarrow{P}$ : Le poids de la barre
• $\overrightarrow{R}$ : La réaction de l’axe

On applique le principe fondamental de la dynamique :

$$\begin{gathered} \sum _{}^{}{\mathcal{M}}_{\left(\Delta \right)}\left(\overrightarrow{F}\right)=J_{\Delta }.\ddot{\theta } \\ {\mathcal{M}}_{\left(\Delta \right)}\left(\overrightarrow{P}\right)+{\mathcal{M}}_{\left(\Delta \right)}\left(\overrightarrow{R}\right)=J_{\Delta }.\ddot{\theta } \\ -P.OM=J_{\Delta }.\ddot{\theta } \\ -m.g.d.\sin \theta =J_{\Delta }.\ddot{\theta } \\ -m.g.d.\theta =J_{\Delta }.\ddot{\theta } \left(\sin \theta \approx \theta \right) \\ \overline{)\ddot{\theta }+\frac{mgd}{J_{\Delta }}\theta =0} \end{gathered}$$

II- Pendule pesant

2-2/ Équation horaire du mouvement

L'équation du mouvement est : $\ddot{\theta }+\frac{mgd}{J_{\Delta }}\theta =0$

C’est une équation différentielle linéaire du seconde ordre, sa solution est :

$\theta ={\theta }_m\cos \left(\frac{2\mathrm{\pi }}{T_0}t+\phi \right)={\theta }_m\cos \left({\omega }_{0}t+\phi \right)$

Calcul de $T_0$

$$\begin{gathered} \theta ={\theta }_m\cos \left({\omega }_{0}t+\phi \right) \\ \Rightarrow \dot{\theta }=-{\theta }_m{\omega }_0\sin \left({\omega }_{0}t+\phi \right) \\ \Rightarrow \ddot{\theta }=-{\theta }_m{{\omega }_0}^2\cos \left({\omega }_{0}t+\phi \right)=-{{\omega }_0}^2.\theta \\ \Rightarrow {{\omega }_0}^2=\frac{mgd}{J_{\Delta }} \\ \Rightarrow {\omega }_0=\sqrt{\frac{mgd}{J_{\Delta }}}=\frac{2\mathrm{\pi }}{T_0} \\ \Rightarrow \overline{){\mathrm{T}}_0=2\mathrm{\pi }\sqrt{\frac{{\mathrm{J}}_{\mathrm{\Delta }}}{\mathrm{mgd}}}} \end{gathered}$$

III- Pendule simple

3-1/ Équation différentielle du mouvement

Le pendule simple est une masse ponctuelle fixée à l'extrémité d'un fil sans masse et inextensible, et oscillant sous l'effet de la pesanteur.

Il s'agit du modèle de pendule pesant le plus simple.

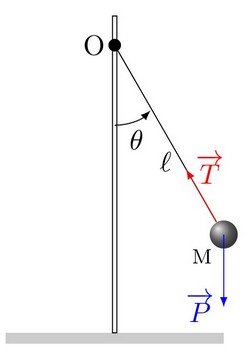
Le bilan des forces :

• $\overrightarrow{P}$ : Le poids de la masse
• $\overrightarrow{T}$ : La tension du fil

On applique le principe fondamental de la dynamique :

$$\begin{gathered} \sum _{}^{}{\mathcal{M}}_{\left(\Delta \right)}\left(\overrightarrow{F}\right)=J_{\Delta }.\ddot{\theta } \\ {\mathcal{M}}_{\left(\Delta \right)}\left(\overrightarrow{P}\right)+{\mathcal{M}}_{\left(\Delta \right)}\left(\overrightarrow{T}\right)=J_{\Delta }.\ddot{\theta } \\ -P.l.\sin \theta =J_{\Delta }.\ddot{\theta } \\ -m.g.l.\theta =m.l^2.\ddot{\theta } \left(\sin \theta \approx \theta \right) \\ \overline{)\ddot{\theta }+\frac{g}{l}\theta =0} \end{gathered}$$

III- Pendule simple

3-2/ Équation horaire du mouvement

II- Pendule pesant

2-2/ Équation horaire du mouvement

L'équation du mouvement est : $\ddot{\theta }+\frac{g}{l}\theta =0$

C’est une équation différentielle linéaire du seconde ordre, sa solution est :

$\theta ={\theta }_m\cos \left(\frac{2\mathrm{\pi }}{T_0}t+\phi \right)={\theta }_m\cos \left({\omega }_{0}t+\phi \right)$

Calcul de $T_0$

$$\begin{gathered} \theta ={\theta }_m\cos \left({\omega }_{0}t+\phi \right) \\ \Rightarrow \dot{\theta }=-{\theta }_m{\omega }_0\sin \left({\omega }_{0}t+\phi \right) \\ \Rightarrow \ddot{\theta }=-{\theta }_m{{\omega }_0}^2\cos \left({\omega }_{0}t+\phi \right)=-{{\omega }_0}^2.\theta \\ \Rightarrow {{\omega }_0}^2=\frac{g}{l} \\ \Rightarrow {\omega }_0=\sqrt{\frac{g}{l}}=\frac{2\mathrm{\pi }}{T_0} \\ \Rightarrow \overline{){\mathrm{T}}_0=2\mathrm{\pi }\sqrt{\frac{\mathrm{l}}{g}}} \end{gathered}$$

IV- Oscillations forcées et résonance

4-1/ Définition

Les frottements agissent sur les oscillations mécaniques et leur mouvement devient amortie, et on peut entretenir leur mouvement en récompensant l'énergie dissipée par une méthode convenable à l'oscillateur.

On lie l'oscillateur avec un appareil qui lui fournit l'énergie nécessaire pour que son mouvement soit entretenu.

Cet appareil s'appelle l'excitateur, c'est un système ayant un mouvement oscillatoire qui impose sa période $T_e$ à l'oscillateur qui s’appelle (résonateur) et le mouvement de ce dernier devient forcé.

IV- Oscillations forcées et résonance

4-2/ Exemple d'oscillations forcées

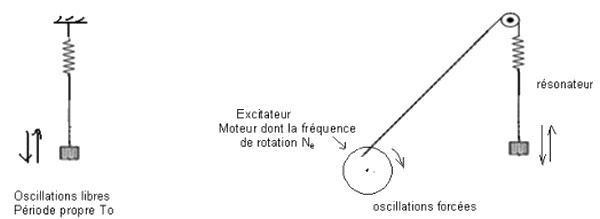
Dans cet exemple le pendule joue le rôle du résonateur, sa fréquence propre est $N_0$ alors que le moteur joue le rôle de l’excitateur de fréquence $N_e$.

En liant l’oscillateur mécanique avec le moteur, il s'oblige d'osciller avec une fréquence égale à celle du moteur.

IV- Oscillations forcées et résonance

4-3/ Phénomène de résonance

En faisant varier la fréquence du moteur, on obtient la plus grande amplitude du résonateur lorsque la fréquence du moteur (excitateur) est égale à la fréquence propre du pendule élastique (résonateur), on dit qu’il y’a résonance.

À la résonance on a $N_e=N_0$, avec $N_0=\frac{1}{T_0}=\frac{1}{2\mathrm{\pi }}\sqrt{\frac{K}{m}}$

Si l'amortissement est faible, le phénomène de résonance est plus clair (aigu).

Si l'amortissement est fort, le phénomène de résonance est flou.

V- Exercices

5-1/ Exercice 1

Un pendule de torsion est constitué par un fil métallique vertical, fixé à l’une des extrémités un disque horizontal, homogène de masse $M=5,60kg$ et de diamètre $d=24cm$, l’autre extrémité du fil est étant fixé à un support.

Le système (disque+fil) peut tourner autour d’un axe fixe $(∆)$ matérialisé par le fil métallique.

Lorsqu'on applique une force d’intensité $4,23N$ et de direction tangente à la gante du disque, ce dernier tourne d’un angle $\theta =3,34°$ de sa position d’équilibre stable.

Puis on enlève cette force et on lâche le système sans vitesse initiale.

1. Calculer la constante de torsion $C$ du fil métallique

2. En appliquant la relation fondamentale de la dynamique, établir l’équation différentielle du mouvement du système.

La solution de l’équation différentielle s’écrit de la forme suivante : $\theta \left(t\right)={\theta }_m\cos (\frac{2\mathrm{\pi }}{{\mathrm{T}}_0}t + {\phi }_0)$

3. Déterminer l’expression de la période propre $T_0$ des oscillations et la fréquence $f_0$ et les calculer.

4. Écrire l’équation horaire du mouvement $\theta \left(t\right)$.

5. Quelle est la nature de ce mouvement ?

V- Exercices

5-2/ Exercice 2

Une barre horizontale $AB$ est supportée par un fil vertical de constante de torsion $C$ dont une des extrémité est fixée au centre de gravité $G$ de $AB$, et l’autre extrémité est attachée à un point fixe $O$.

Deux masse ponctuelles de même masse sont placées sur l’axe $AB$ de la barre.

Le moment d’inertie du système (tige + deux masses) par rapport à un axe $\left(∆\right)$ matérialisé par le fil vertical est $J_{∆}=1,46kg.m^2$.

La période propre du pendule de torsion en absence de frottement est $T_0=7min$.

Étude du pendule de torsion

On néglige tous les frottement et l’angle de torsion sera noté par $\theta$, la vitesse angulaire par $\frac{d\theta }{dt}$ et l’accélération angulaire par $\frac{d^2\theta }{d{t}^2}$.

1. Établir l’équation différentielle vérifiée par l’angle de torsion $\theta$ au cours des oscillations du pendule de torsion.

La solution de cette équation différentielle s’écrit sous la forme : $\theta \left(t\right)={\theta }_m\cos (\frac{2\pi }{T_0}t+\phi )$.

2. En utilisant l’équation différentielle et sa solution, trouver l’expression de la période propre $T_0$ du pendule en fonction de $C$ et $J_{∆}$.

3. En déduire la valeur de la constante de torsion $C$ du fil utilisé dans cette expérience.

Exploitation de la représentation $\theta =f\left(t\right)$

On réalise deux expériences pour mesurer la période propre du pendule, l’une avec frottements, l’autre en absence de frottements.

Les deux courbes (a) et (b) de la figure suivante représentent la variation de $\theta$ en fonction de $t$ dans chaque cas :

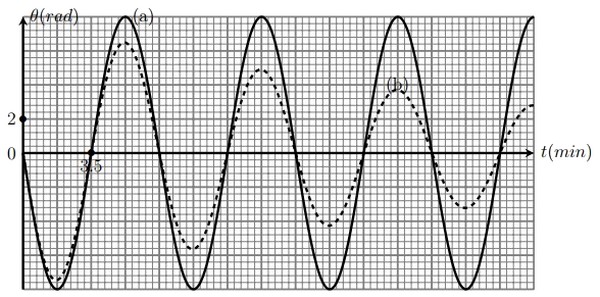
4. Indiquer, en justifiant votre réponse, la courbe correspond au régime pseudopériodique

5. Déterminer, en utilisant la figure ci-dessus en absence des frottements, la valeur de la vitesse angulaire du mouvement du pendule de torsion à l’instant $t=0$.

V- Exercices

5-3/ Exercice 3

Un pendule pesant est constitué d’une boule homogène de rayon $r=2,5cm$ et de masse $m=200g$ et d’une tige homogène de même masse que la boule et de longueur $L=10r$, l’une des extrémités est soudée à la boule au point $A$.

Le système (Tige+boule) peut tourner autour d’un axe fixe $(∆)$ passant par le point $O$ de l’autre extrémité de la tige :

On néglige tous les frottements et on prend $g=10m.s^{-2}$

Le moment d’inertie du système par rapport à l’axe $(∆)$ est $J_{∆}={10}^{-2}kg.m^2$.

On écarte le système de sa position d’équilibre stable d’un angle de ${\theta }_m=10°$, puis on le lâche sans vitesse initiale à la date $t=0$.

1)En appliquant la relation fondamentale de la dynamique au système, montrer que l’équation différentielle du mouvement du système s’écrit sous la forme suivante :

$\ddot{\theta }+\left(\frac{16m.g.r}{J_{∆}}\right).\theta =0$

2. Quelle est la nature du mouvement du système.

3. Calculer la période propre du mouvement.

4. Déterminer l’équation horaire du mouvement de système.