PC 2Bac SPC - Examen National 2021 Normale

Exercice I : Chimie (7 pts)

Les parties 1 et 2 sont indépendantes

Partie l : Étude cinétique d’une réaction chimique

L'une des plus anciennes réactions de synthèse est la fabrication du savon. Le savon est un produit composé de molécules obtenues par réaction chimique, entre un composé organique et une solution aqueuse d’hydroxyde de sodium.

Cette partie de l’exercice se propose d’étudier, par conductimétrie, la cinétique de la réaction de synthèse d’un savon. Cette réaction se produit entre l’éthanoate d’éthyle de formule $C{H}_{3}COO{C}_2{H}_5$ et une solution aqueuse d’hydroxyde de sodium $N{a}_{\left(aq\right)}^{+}+H{O}_{\left(aq\right)}^{-}$.

À un instant choisi comme origine des dates $t=0$, on introduit, en excès, l’éthanoate d’éthyle dans un ballon contenant une quantité de matière $n_0\left(H{O}^{-}\right)={10}^{-3}mol$ d’ions hydroxyde. On obtient un mélange réactionnel ayant un volume $V_0=100mL$.

Il se produit, sous une température constante, une réaction modélisée par l’équation chimique suivante : $C{H}_{3}COO{C}_2{H}_{5\left(aq\right)}+H{O}_{\left(aq\right)}^{-}\to C{H}_{3}CO{O}_{\left(aq\right)}^{-}+C_2{H}_{5}O{H}_{\left(aq\right)}$

1)Dresser le tableau d’avancement de cette réaction et déterminer la valeur de l’avancement final $x_f$ sachant que cette réaction est totale.

2) On mesure, à chaque instant, la conductivité $\sigma$ du mélange réactionnel. La courbe de la figure 1 donne les variations de la conductivité du mélange réactionnel en fonction du temps :

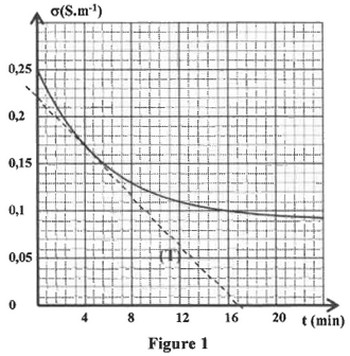
La droite $\left(T\right)$ représente la tangente à la courbe au point d’abscisse $t_1=4min$.

L’expression de la conductivité $\sigma$ du mélange réactionnel en fonction de l’avancement $x$ de la réaction est : $\sigma =0,25-160.x$ où $\sigma$ est exprimée en $S.m^{-1}$ et $x$ en $mol$.

2.1)Définir le temps de demi-réaction $t_{1/2}$.

2.2) A l’aide de l’expression $\sigma =f\left(x\right)$ et de la courbe de la figure 1, déterminer la valeur de $t_{1/2}$.

2.3) Montrer que la vitesse volumique de la réaction à un instant $t$ s’écrit sous la forme $v=-\frac{1}{160.V_0}.\frac{d\sigma }{dt}$.

2.4) Déterminer, en $mol.m^{-3}.mi{n}^{-1}$, la valeur $v_1$ de cette vitesse à l’instant $t_1=4min$.

Partie 2 : Étude d’une solution aqueuse d’un acide carboxylique

Un flacon, dont l’étiquette est illisible, contient une solution aqueuse Sa d’un acide carboxylique de formule et de concentration inconnues. Cette partie de l’exercice se propose de :

• déterminer la concentration de cette solution aqueuse.
• identifier cet acide.

On notera $AH$ pour désigner l’acide carboxylique et $A^{-}$ pour désigner sa base conjuguée.

Toutes les mesures sont réalisées à $25°C$.

1) Dosage de l’acide carboxylique

On dose un volume $V_a=20mL$ de la solution aqueuse $S_a$ de concentration $C_a$ par une solution aqueuse $S_b$ d’hydroxyde de sodium $N{a}_{\left(aq\right)}^{+}+H{O}_{\left(aq\right)}^{-}$ de concentration $C_b={10}^{-1}mol.L^{-1}$.

La courbe de la figure 2 représente les variations du $pH$ du mélange réactionnel en fonction du volume $V_b$ de la solution basique versée :

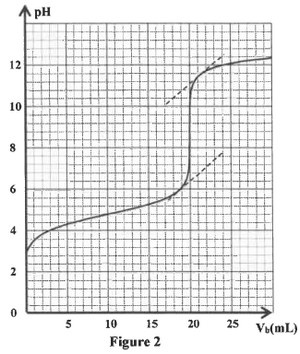
1.1) Écrire l’équation de la réaction du dosage.

1.2) Déterminer graphiquement les coordonnées $p{H}_E$ et $V_{bE}$ du point d’équivalence.

1.3) Déterminer la valeur de la concentration $C_a$.

2) Identification de l’acide carboxylique

La solution $S_a$ est préparée par dissolution de l’acide $AH$ dans l’eau. La mesure du $pH$ de la solution $S_a$ donne : $pH=2,88$.

2.1) Écrire l’équation de la réaction de l’acide $AH$ avec l’eau.

2.2) Montrer que le taux d’avancement final de la réaction est $\tau \approx 1,32\%$.

2.3) Déterminer l’expression du quotient de la réaction $Q_{r,éq}$ à l’équilibre en fonction de $C_a$ et $\tau$. Vérifier que sa valeur est $Q_{r,éq}\approx 1,77.{10}^{-5}$.

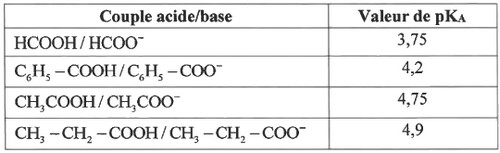
2.4) Identifier l’acide carboxylique $AH$ étudié en vous aidant du tableau des valeurs de $P{K}_A$ des couples acide/base ci-dessous. Justifier votre réponse.

3) Déterminer le volume $V_{b1}$ de la solution $S_b$ versée, au cours du dosage, pour que $\frac{\left[A{H}_{\left(aq\right)}\right]}{\left[A_{\left(aq\right)}^{-}\right]}=2,24$.

Exercice II : Propagation des ondes lumineuses (3 pts)

Un faisceau cylindrique de lumière blanche, émis par une source $S$, arrive perpendiculairement à la face d’un prisme $\left(P\right)$ en verre. Le faisceau lumineux issu du prisme arrive sur un écran $\left(E\right)$. On observe alors sur cet écran un spectre lumineux :

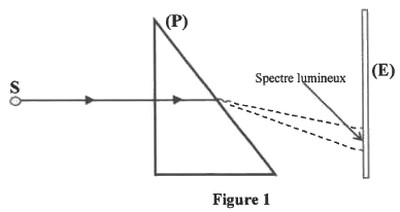
1) Choisir parmi les propositions suivantes, celle qui est juste.

L’expérience précédente montre que la lumière blanche :

• A- est monochromatique
• B- n’est formée que de deux radiations différentes
• C- est polychromatique

2) On éclaire le prisme $\left(P\right)$ successivement par deux radiations lumineuses : l’une est rouge et l’autre est jaune.

Données :

• La célérité de la lumière dans le vide : $c=3.{10}^{8}m.s^{-1}$.
• La longueur d’onde de la radiation rouge dans le prisme est : ${\lambda }_r=474nm$.
• La fréquence de la radiation rouge est : ${\mathcal{v}}_r=3,91.{10}^{14}Hz$.
• Les longueurs d’onde de la radiation jaune : ${\lambda }_{oj}=589nm$ dans le vide et ${\lambda }_j=355nm$ dans le prisme $\left(P\right)$.

2.1) Calculer la fréquence ${\mathcal{v}}_j$ de la radiation jaune.

2.2) Calculer les célérités $v_j$ et $v_r$ des radiations jaune et rouge dans le prisme.

2.3) Quelle propriété du prisme est mise en évidence par les résultats de la question 2.2 ?

3) On éclaire, avec une radiation laser ayant une longueur d’onde $\lambda$, une fente fine horizontale de largeur $a=0,06mm$. On observe sur un écran, placé à une distance $D$ de la fente, un ensemble de taches de direction verticale. La tache centrale a une largeur $L$ (figure 2) :

On change la distance $D$ et on mesure à chaque fois la largeur $L$.

La courbe de la figure 3 donne les variations de $L$ en fonction de $D$ :

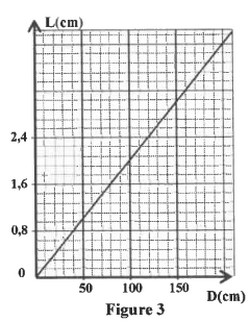
3.1) Établir l’expression de $L$ en fonction de $\lambda$, $a$ et $D$. ($\theta$ étant petit, on prend $\tan \theta =\theta$).

3.2) En exploitant la courbe $L=f\left(D\right)$, montrer que $\lambda =600nm$.

On fixe l’écran à une distance $D_1=2m$ de la fente, et on remplace la fente par un cheveu fin de diamètre $d$. On obtient alors, avec la même radiation de longueur d’onde $\lambda$, une tache centrale de largeur $L_1=3cm$.

3.3) Déterminer le diamètre $d$ du cheveu.

Exercice III : Désintégration du plutonium 238 (2,5 pts)

Le stimulateur cardiaque (pacemaker) est un dispositif qui, une fois implanté dans l'organisme, fournit des impulsions électriques destinées à stimuler les muscles cardiaques. Ces impulsions permettent d'accélérer la pulsation du cœur lorsqu’il est trop lent. Certains stimulateurs cardiaques fonctionnent à partir de l'énergie libérée lors de la désintégration alpha des noyaux du plutonium 238.

Cet exercice se propose d’étudier un stimulateur cardiaque au plutonium 238.

Données :

1) Écrire l’équation de désintégration alpha du plutonium 238 en identifiant le noyau fils.

2) La courbe de la figure suivante représente l’évolution de l’activité $a\left(t\right)$ d’un échantillon de plutonium 238, présent dans  un stimulateur cardiaque. On choisit l’instant d’implantation de ce stimulateur dans  l’organisme d’un patient comme origine des  dates $t=0$ :

2.1) Déterminer graphiquement la demi-vie $t_{1/ 2}$ du plutonium 238.

2.2) En déduire que la valeur de la constante radioactive $\lambda$ est : $\lambda \approx 7,88.{10}^{-3}an{s}^{-1}$ .

2.3) Trouver le nombre $N_0$ de noyaux de plutonium 238, présents à $t=0$, dans ce stimulateur cardiaque, (on prend $1an=365jours$).

3) On considère que ce stimulateur fonctionne de façon efficace lorsque le nombre de noyaux de plutonium 238 qui se désintègrent ne dépasse pas $30\%$ du nombre de noyaux présents dans l’échantillon à $t=0$. Déterminer, en ans, la durée maximale $t_{max}$ du fonctionnement efficace du stimulateur cardiaque.

Exercice IV : Électricité (4,75 pts)

Les circuits des appareils électriques, utilisés dans plusieurs domaines de la vie courante, sont constitués de condensateurs, de bobines, de conducteurs ohmiques, de circuits intégrés...

L’objectif de cet exercice est d’étudier :

• La réponse d’un dipôle RC à un échelon de tension.
• Les oscillations électriques non amorties dans un circuit $LC$.
• La modulation d’amplitude d’un signal.

Partie I - Réponse d’un dipôle RC à un échelon de tension

On réalise le montage, représenté sur le schéma de la figure 1, constitué des éléments suivants :

• un générateur idéal de tension de force électromotrice $E$.
• un condensateur $D$ de capacité $C$ initialement déchargé.
• un conducteur ohmique de résistance $R={10}^3\Omega$.
• un interrupteur $K$.

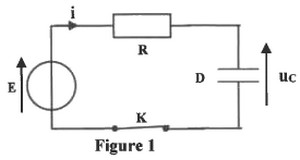
On ferme l’interrupteur à un instant choisi comme origine des dates $\left(t=0\right)$. Un système d’acquisition informatisé permet de tracer la courbe de la figure 2, représentant les variations de $\frac{d{u}_c}{dt}$ en fonction de $u_c$. $u_c$ étant la tension à un instant $t$ aux bornes du condensateur et $\frac{d{u}_c}{dt}$ sa dérivée par rapport au temps :

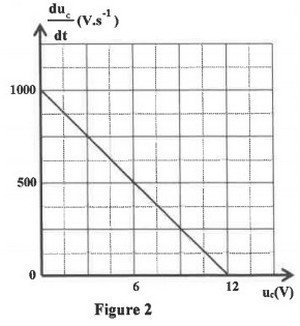
1) Montrer que l’équation différentielle vérifiée par la tension $u_c\left(t\right)$ s’écrit sous la forme $\frac{d{u}_c}{dt}=-\frac{1}{RC}{u}_c+\frac{E}{RC}$.

2) En exploitant la courbe de la figure 2, montrer que la capacité du condensateur est $C=12\mu F$.

Partie II - Oscillations électriques non amorties dans un circuit $LC$

On réalise le montage représenté sur le schéma de la figure 3 :

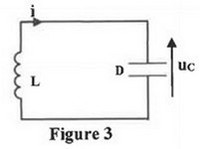
Ce montage est constitué du condensateur précédent $D$, initialement chargé, et d’une bobine d’inductance $L$ et de résistance négligeable. Un système d’acquisition informatisé permet de tracer la courbe représentant l’évolution de la charge $q\left(t\right)$ du condensateur (figure 4) :

1) Préciser, parmi les trois régimes d’oscillations, le régime mis en  évidence par la courbe de la figure 4.

2) Établir l’équation différentielle vérifiée par la charge $q\left(t\right)$ du condensateur.

3) Trouver l’expression de la période propre $T_0$ de l’oscillateur en fonction de $L$ et de $C$ pour que l’expression $q\left(t\right)=Q_m.\cos \left(\frac{2\mathrm{\pi }}{T_0}t\right)$ soit solution de cette équation différentielle.

4) Déterminer graphiquement la valeur de $T_0$.

5) En déduire la valeur de $L$. (on prends ${\mathrm{\pi }}^2=10$).

Partie III - Modulation d’amplitude d’un signal

Pour obtenir un signal modulé en amplitude, on réalise le montage représenté sur le schéma de la figure 5 où le multiplieur $X$ est un circuit intégré possédant deux entrées $E_1$ et $E_2$ et une sortie $S$ :

On applique :

• sur l’entrée $E_1$ une tension $u_1\left(t\right)$ ayant pour expression $u_1\left(t\right)=P_m\cos (2\mathrm{\pi }{F}_p.t)$.
• sur l’entrée $E_2$ une tension $u_2\left(t\right)$ ayant pour expression $u_2\left(t\right)=U_0+s\left(t\right)$ où $s\left(t\right)=S_m\cos (2\mathrm{\pi }{f}_s.t)$ est la tension modulante et $U_0$ est la composante continue de cette tension.

On obtient à la sortie $S$ du multiplieur $X$ une tension $u_s\left(t\right)$ modulée en amplitude.

On visualise la tension $u_1\left(t\right)$ sur la voie $A$ de l’oscilloscope et la tension $u_2\left(t\right)$ sur la voie $B$ (figure 6) :

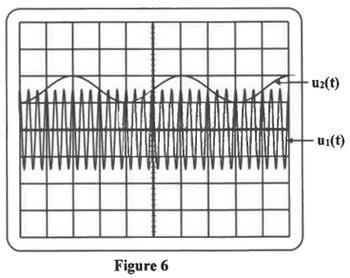
Données :

• Sensibilité verticale : $1V/div$
• Sensibilité horizontale : $2ms/div$

1) Définir la modulation d’amplitude.

2) Déterminer graphiquement :

• 2.1) les fréquences $F_p$ et $f_s$.
• 2.2) la valeur de $S_m$ et celle de $U_0$.

3) La modulation réalisée dans ce cas sera-t-elle de bonne qualité ? Justifier votre réponse.

Exercice V : Étude du mouvement d’un parachutiste (2,75 pts)

Le parachute est un dispositif destiné, après son ouverture, à freiner le mouvement d'un parachutiste en chute verticale dans l’air.

Cet exercice se propose d’étudier un modèle simplifié du mouvement d’un parachutiste. Ce dernier se laisse tomber sans vitesse initiale d’un hélicoptère en vol stationnaire situé à une hauteur h au-dessus du sol.

On étudie le mouvement du centre d’inertie $G$ du système $\left(S\right)$, constitué d’un parachutiste équipé de son parachute, dans le repère $\left(O,\overrightarrow{k}\right)$ lié à un référentiel terrestre considéré comme galiléen (figure 1) :

On considère que la trajectoire de $G$ est verticale et que l’accélération de la pesanteur reste constante.

Données :

• La masse du système $\left(S\right)$ : $m=100kg$.
• L’accélération de la pesanteur : $g=10m.s^{-2}$.
• La hauteur $h$ : $h=660m$.

Le mouvement du système s’effectue en deux phases.

Phase 1 : parachute fermé

Le parachutiste se laisse tomber de l’hélicoptère sans vitesse initiale à un instant choisi comme origine des dates $\left(t=0\right)$. La chute se fait durant cette phase avec le parachute fermé.

On modélise l'évolution de la vitesse du centre d’inertie $G$ du système  $\left(S\right)$ durant cette phase par la courbe de la figure 2 :

1.1) Quelle est la nature du mouvement de $G$ ? justifier votre réponse.

1,2) Peut-on considérer que le mouvement du parachutiste, durant cette phase, est une chute libre ? Justifier votre réponse.

Phase 2: parachute ouvert

Le parachutiste ouvre son parachute après une durée $\Delta t_1=4s$ depuis le début de sa chute. On choisit l’instant d’ouverture du parachute comme nouvelle origine des dates pour cette phase.

Durant cette phase, le système est soumis à son poids et aux frottements de l’air modélisés par une force de contact $\overrightarrow{F}=-\alpha .v^2.\overrightarrow{k}$ avec $v$ la vitesse de $G$ et $\alpha$ une constante positive.

On modélise l’évolution de la vitesse de $G$ durant cette phase par la courbe de la figure 3 :

2.1) Montrer que l’équation différentielle vérifiée par la vitesse $v$ s’écrit $\frac{dv}{dt}+\frac{\alpha }{m}.v^2=g$.

2.2) Trouver l’expression de la vitesse limite $V_{\mathcal{l}}$ du mouvement en fonction de $m$, $g$ et $\alpha$.

2.3) Déterminer graphiquement $V_{\mathcal{l}}$.

2.4) En déduire la valeur de $\alpha$.

3) Sachant que la durée totale du mouvement de $G$ depuis le début de la chute jusqu’à l’arrivée au sol st $\Delta t=70s$, trouver la distance $d$ parcourue par $G$ durant le régime initial de la phase 2.