
Physique et Chimie : 2ème Année Bac SMA-SMB
Examen National 2021 Normale
Professeur : Mr El GOUFIFA Jihad
I- Exercice 1 : Chimie (7 pts)
Les parties I et II sont indépendantes
Partie I : A propos de l’acide formique
L'acide carboxylique le plus simple est l'acide méthanoïque ou formique Dans la nature, on le trouve dans les orties et dans le venin de plusieurs insectes comme les abeilles et les fourmis.
Quand une fourmi pique un corps, elle injecte, à chaque piqûre, environ un volume d’une solution , ce qui représente la majorité du volume total de la solution urticante disponible dans l’abdomen d’une "fourmi typique”. Le volume d’acide méthanoïque contenu dans la solution représente 50 % de .
Données :
- Masse volumique de l’acide méthanoïque :
- Masses molaires : ;
- Couples acide/base : ;
1) Montrer que la quantité de matière d’acide méthanoïque qu’une fourmi typique injecte à chaque piqûre est . (0,5pt)
2) L’hydrogénocarbonate de sodium est souvent utilisé pour traiter les piqûres de fourmis.
2-1/ Écrire l'équation correspondant à la réaction entre l’hydrogénocarbonate de sodium et l'acide méthanoïque (cette réaction est supposée totale). (0,5pt)
2-2/ Déterminer la masse d’hydrogénocarbonate de sodium nécessaire pour réagir complètement avec la quantité de matière de l’acide contenu dans la solution injectée. (0,75pt)
3) Dès que la solution est injectée, elle se dilue dans l’eau du corps pour produire une solution aqueuse d’acide méthanoïque . On considère que la solution injectée se dissout immédiatement dans d’eau du corps. On néglige dans le calcul le volume d’acide méthanoïque injecté. Le de la solution est .
3-1/ Déterminer le pourcentage de molécules d’acide méthanoïque qui réagit dans la solution . Écrire alors l’équation de la réaction de l’acide méthanoïque avec l’eau. (0,5pt)
3-2/ Montrer que le du couple est . (0,5pt)
4) On prépare une solution aqueuse d’acide méthanoïque de même concentration molaire que la solution .
4-1/ On ajoute d’eau distillée à de la solutions . Trouver la valeur du de la solution obtenue. (0,5pt)
4-2/ On ajoute d’une solution aqueuse d’hydroxyde de sodium de concentration molaire à de la solutions .
4-2-1- Écrire l’équation de la réaction qui se produit. (0,5pt)
4-2-2- Déterminer la valeur du du mélange réactionnel. (0,75pt)
Partie II : Étude de la pile plomb-fer
On étudie la pile de deux plomb-fer qui fait intervenir les deux couples ox/red : et .
On la constitue de deux compartiments liés par un pont salin.
Le premier compartiment est constitué d’une lame de plomb plongée dans un volume d’une solution aqueuse de nitrate de plomb de concentration molaire initiale . Le deuxième compartiment est constitué d’une lame de fer plongée dans un volume d'une solution aqueuse de chlorure est de fer (II) de concentration molaire initiale .
La partie immergée de la lame de fer dans la solution est en excès.
Données :
- Le faraday :.
- Masse molaire du plomb : .
On monte en série avec la pile un conducteur ohmique , un ampèremètre et un interrupteur .
A un instant de date , on ferme le circuit, l’ampèremètre indique alors le passage d’un courant électrique d’intensité considérée constante.
On négligera l’oxydation des ions par le dioxygène dissous dans l’eau.
Au cours du fonctionnement de la pile, la masse de la lame de plomb a augmenté de après une durée de fonctionnement .
1) Donner le nombre d’affirmations fausses parmi les affirmations suivantes : (0,5 pt)
- a- La réduction se produit au niveau de l’électrode de fer.
- b- L’oxydation se produit au niveau de l’électrode de plomb.
- c-La lame de fer représente la cathode et c’est le pôle négatif de la pile,
- d- La lame de plomb représente l’anode et c’est le pôle négatif de la pile.
2) Écrire l’équation bilan lors du fonctionnement de la pile. (0,5 pt)
3) Déterminer à l’instant , le quotient de réaction lors du fonctionnement de la pile. (0,75 pt)
4) Sachant que l’intensité du courant est , trouver la valeur de l’instant . (0,75 pt)
II- Exercice 2 : Ondes - Vérification de la pureté d’une huile (2 pts)
La célérité du son dans une huile végétale dépend de sa pureté. La valeur de la célérité du son dans une huile d’olive pure se situe entre et .
Pour tester une huile d’olive au laboratoire, on utilise le montage de la figure l qui permet de comparer les durées de parcours d’une onde ultrasonore dans des milieux différents.
L’émetteur d’ultrasons génère simultanément deux salves d’ondes. Les récepteurs et sont reliés à une interface d’acquisition qui déclenche l’enregistrement des signaux dès que le récepteur détecte en premier les ultrasons. L’huile testée est disposée dans un tube en verre entre l’émetteur et le récepteur , tandis que l’air sépare l’émetteur du récepteur (figure 1) :

Pour chaque valeur de la longueur du tube on mesure, par l’intermédiaire du système informatique, la durée écoulée entre les deux signaux reçus en et .
A partir de ces mesures on obtient la courbe de la figure 2 représentant les variations de en fonction de :
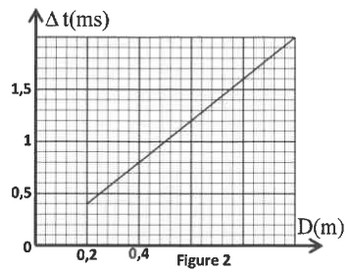
1) Les ondes ultrasonores sont-elles des ondes longitudinales ou transversales ? Justifier. (0,5pt)
Les ultrasons utilisés dans l’expérience précédente ont une fréquence de . Leur célérité dans l’air est .
2) Calculer la distance parcourue par ces ultrasons dans l’air pendant une période. (0,5pt)
3) Exprimer en fonction de , et . (0,5pt)
4) L’huile testée est-t-elle pure ? Justifier. (0,5pt)
III- Exercice 3 : Transformations nucléaires - Stabilité des noyaux, réaction de fission (1,5 pts)
Données
- Masse des particules :
- Énergie de liaison de la particule :
- Masse du neutron :
- Masse du proton :
1- Diagramme de Segré
La figure 1 représente le diagramme de Segré dont lequel les noyaux stables correspondent aux cases grisées dans le diagramme :

Donner le nombre d’affirmations justes : (0,5pt)
- a- La non stabilité d’un noyau peut être due au grand nombre de nucléons qu’il contient.
- b- La stabilité d’un noyau peut être due au grand nombre de neutrons par rapport au nombre de protons qu’il contient.
- c- Les isotopes d’un même élément se trouvent sur la même ligne dans le diagramme de Segré .
- d-Les noyaux , et sont radioactifs .
- e- Le noyau est stable.
2- Fission nucléaire
1) Écrire l’équation de la réaction nucléaire correspondant au bombardement d’un noyau de bore par un neutron pour former une particule et un noyau de lithium en déterminant et . (0,25pt)
2) Comparer la stabilité de la particule avec celle du . (0,5pt)
3) Calculer, en unité , l’énergie libérée par la fission d’un noyau de bore 10. (0,25pt)
IV- Exercice 4 : Électricité (5 pts)
Cet exercice vise l’étude de :
- La charge d'un condensateur et sa décharge dans une bobine.
- La modulation et la démodulation d'amplitude d'une onde électromagnétique.
1- Charge d’un condensateur et sa décharge dans une bobine
On réalise le montage représenté sur le schéma de la figure 1. Ce montage comprend :
- un générateur idéal de courant.
- un condensateur de capacité variable, initialement non chargé.
- une bobine d’inductance et de résistance .
- un microampèremètre.
- un interrupteur .
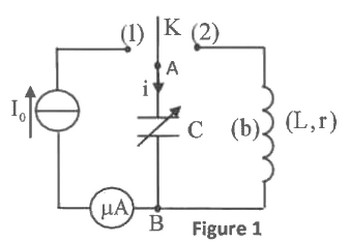
On ajuste la capacité du condensateur sur une valeur .
On place l’interrupteur en position (1) à un instant de date . Le microampèremètre indique . Un système de saisie informatique convenable permet d’avoir le graphe de la figure 2 représentant avec étant l’énergie électrique emmagasinée dans le condensateur à un instant :
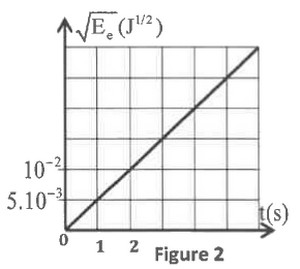
1-1/ Donner l’expression de l’énergie emmagasinée dans le condensateur en fonction de sa charge et de sa capacité . (0,25pt)
1-2/ Montrer que . (0,75pt)
1-3/ Lorsque la tension aux bornes du condensateur prend la valeur , on place l’interrupteur en position (2) à un instant choisi comme une nouvelle origine des dates . Un dispositif approprié permet de visualiser la courbe donnant les variations au cours du temps de l’intensité du courant dans le circuit (figure 3) :
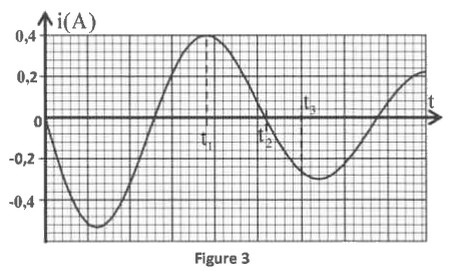
1-3-1- Calculer l’énergie dissipée par effet joule dans le circuit entre les instants et (figure 3). (0,75pt)
1-3-2- Indiquer, en justifiant, si le condensateur se charge ou se décharge entre les instants et (figure 3). (0,5pt)
2- Modulation et démodulation d’amplitude d’une onde électromagnétique
On peut transmettre une information à grande distance, en modulant l’amplitude d’une onde électromagnétique qui se propage d'un émetteur à un récepteur.
L’émetteur doit assurer la production de l’onde électromagnétique et sa modulation pour porter le signal informatif. Quant au récepteur, il doit être conçu pour démoduler fonde et récupérer le signal informatif, fournissant du sens pour l'utilisateur. La modulation d’amplitude consiste à varier l’amplitude de fonde porteuse au cours du temps selon l'évolution temporelle du signal informatif à transmettre.
Afin d’obtenir un signal modulé en amplitude, on utilise un circuit intégré multiplieur (figure 4) :
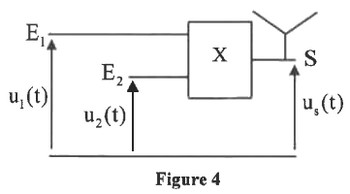
On applique à l’entrée :
- : la tension avec représentant le signal informatif et la tension de décalage.
- : une tension sinusoïdale représentant la porteuse .
La tension de sortie obtenue est ; est une constante qui dépend du circuit intégré .
La tension de sortie ainsi définie s’exprime par avec .
Dans cette expression est l’amplitude de la tension modulée et le taux de modulation.
Un dispositif approprié permet de visualiser simultanément deux des tensions , et . On observe ainsi les oscillogrammes (a) et (b) de la figure 5 :
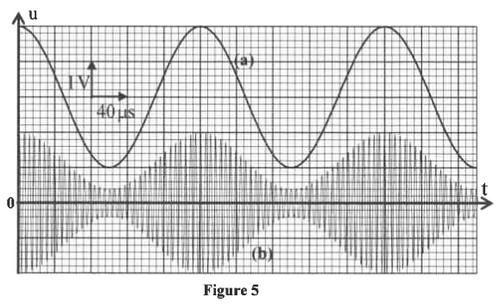
2-1/ Indiquer, en justifiant, pour chacun des oscillogrammes de la figure 5, s’il correspond au signal modulant, au signal modulé ou à la porteuse. (0,5pt)
2-2/ En se basant sur les oscillogrammes de la figure 5, déterminer :
2-2-1- la fréquence de la porteuse et celle du signal informatif. (0,5pt)
2-2-2- le taux de modulation m. (0,5pt)
2-3/ Démodulation de l’onde
La figure 6 schématise un constituant de récepteur radio lié au circuit de démodulation. Ce constituant est équivalent à la bobine précédente d’inductance et de résistance associée au condensateur de capacité variable :
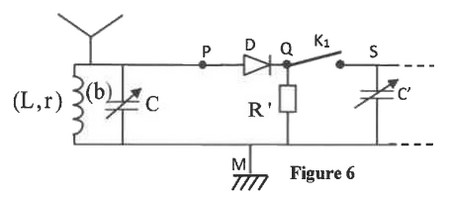
Le circuit formé par la bobine et le condensateur est mis en vibration forcée par l’intermédiaire de l’antenne qui capte toutes les ondes émises par toutes les stations.
Pour écouter une seule station, il suffit d’accorder la fréquence propre du circuit à la fréquence de l’émetteur en régulant la capacité du condensateur. (On prendra : )
2-3-1- Calculer la valeur à laquelle il faut ajuster la capacité de l’élément récepteur pour que la fréquence propre soit . (0,5 pt)
2-3-2- Trouver alors l’intervalle des valeurs de la capacité pour avoir une bonne détection d’enveloppe sachant que la fréquence de l’information émise est et . (0,75pt)
V- Exercice 5 : Mécanique (4,5 pts)
Les parties I et II sont indépendantes.
Partie I : Mouvement d’une luge
On étudie le mouvement d’une luge modélisée par un solide (S) de centre d’inertie G et de masse m dans deux phases de son parcours :
- Première phase : Mouvement rectiligne de (S) sur un plan incliné.
- Deuxième phase : Chute verticale de (S) dans l’eau.
Données :
Masse de la luge : .
Intensité de la pesanteur : .
1- Première phase : Mouvement de la luge sur un plan incliné
On étudie le mouvement du centre d’inertie dans le repère lié à un référentiel terrestre considéré galiléen (figure 1) :
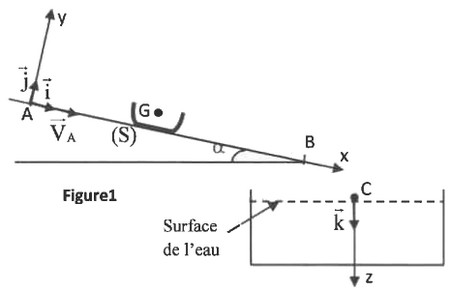
Après la phase de poussée vers le bas, le solide atteint une vitesse au point et glisse sans frottement le long de la piste rectiligne faisant un angle avec l’horizontale. La pente est inclinée à ().
1-1- En appliquant la deuxième loi de Newton, déterminer la valeur de l’accélération du centre d’inertie de . (0,25 pt)
L’origine des dates est choisie à l’instant du passage par le point .
1-2- Trouver la distance parcourue, à partir du point , lorsque la luge atteint la vitesse . (0,5pt)
1-3- On filme le mouvement de la luge, puis on exploite la vidéo avec un logiciel adapté. Ceci a permis de tracer la courbe représentant les variations de la vitesse de en fonction du temps (figure 2) :
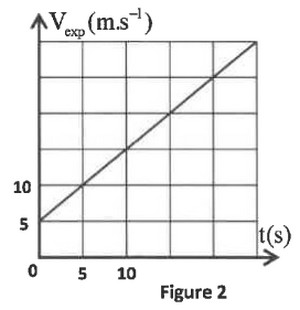
1-3-1- Déterminer graphiquement la valeur expérimentale de l’accélération du centre d’inertie . (0,25pt)
On interprète la différence entre et par l’existence de frottements. On rappelle que lorsque le contact entre le plan incliné et la luge se fait avec frottement solide, la piste exerce sur une force ayant une composante tangentielle et une composante normale .
Lors du mouvement de , les intensités de et de sont liées par la relation , avec une constante appelée coefficient de frottement qui dépend des matériaux en contact et de leur état de surface.
1-3-2- Exprimer le coefficient en fonction de , , et . Calculer sa valeur. (0,5pt)
2- Deuxième phase : Chute verticale de dans l’eau
La luge quitte la piste en et tombe dans un lac au point (figure 1).
Après s’être immobilisée quelques instants, la luge se met à couler verticalement sans vitesse initiale depuis le point .
On étudie le mouvement du centre d’inertie dans un repère lié à un référentiel terrestre considéré comme galiléen (figure 1).
On repère la position de à tout instant par la cote Z de l’axe vertical dirigé vers le bas. L’origine des dates est prise au point .
Au cours de sa chute dans l’eau, la luge est soumise, en plus de son poids, à la force de frottement fluide où et la vitesse de à un instant .
On note que la poussée d’Archimède est négligée.
2-1- Montrer que l’équation différentielle du mouvement de vérifiée par la vitesse s’écrit avec . On donnera et en fonction des paramètres de l’exercice. (0,75pt)
2-2- La solution de l’équation différentielle du mouvement de s’écrit . Trouver, à l’instant la profondeur atteinte par la luge depuis le point , origine de la cote . (0,5pt)
Partie II : Mouvement d’un faisceau de protons dans un champ électrostatique uniforme
On se propose dans cette partie de déterminer les caractéristiques du mouvement d'un proton dans un champ électrique uniforme.
On considère que le mouvement du proton se fait dans le vide et que son poids n’a pas d’influence sur le mouvement.
Un condensateur plan est constitué de deux plaques métalliques parallèles rectangulaires horizontales et de longueur et séparées par une distance (figure 3) :

Les deux plaques sont soumises à une tension . Entre les deux plaques, règne alors un champ électrostatique uniforme .
Le mouvement du proton est étudié dans le repère orthonormé lié à un référentiel terrestre supposé galiléen.
Un faisceau de protons pénètre entre les deux plaques au point avec la vitesse faisant un angle avec . On prend l’instant où le proton passe par comme origine des dates . Le proton pénétré en est soumis, au cours de son mouvement le long de la distance à la force électrostatique avec la charge du proton.
Données :
- Masse du proton :
On rappelle que
Le faisceau de protons sort du champ électrostatique en du condensateur.
1) En appliquant la deuxième loi de Newton, établir les équations horaires et du mouvement du proton en fonction de et des paramètres de l’exercice. (0,5 pt)
2) Déduire l’équation de la trajectoire du proton. (0,25 pt)
3) Déterminer la valeur de la tension pour que le faisceau sorte effectivement en . (0,5 pt)
4) Déterminer à quelle distance minimale de la plaque supérieure passe le faisceau de proton. (0,5 pt)


