PC 2Bac SVT-STE-STM - Examen National 2021 Normale

I- Chimie (7 pts)

Les parties 1 et 2 sont indépendantes

Les transformations chimiques d’oxydo-réduction ou d’acide-base permettent de reconnaître les effets de certaines solutions acides sur les métaux, de suivre l’évolution temporelle d’un système chimique et d’étudier les solutions aqueuses acides ou basiques.

Cet exercice vise :

• le suivi temporel de l’évolution d’un système chimique.
• la détermination de la constante d’acidité d’un couple (acide/base).

Partie 1 : Suivi temporel de l’évolution d’un système chimique

On réalise une expérience en introduisant, à l’instant $t_0=0$, une masse de zinc en poudre de valeur $m\left(Zn\right)=1,0g$ dans un ballon contenant le volume $V=40mL$ d’une solution aqueuse $\left(S\right)$ d’acide chlorhydrique $H_3{O}_{\left(aq\right)}^{+}+C{l}_{\left(aq\right)}^{-}$ de concentration molaire $C_A=0,5mol.L^{-1}$.

Les ions $H_3{O}_{\left(aq\right)}^{+}$ réagissent avec le zinc $Z{n}_{\left(s\right)}$ suivant la réaction chimique d’équation $2H_3{O}_{\left(aq\right)}^{+}+Z{n}_{\left(s\right)}\to H_{2\left(g\right)}+Z{n}_{\left(aq\right)}^{2+}+2H_2{O}_{\left(l\right)}$

La mesure du volume de dihydrogène formé permet le suivi de l'évolution temporelle de l’avancement $x$ de la réaction et de tracer le graphe $x=f\left(t\right)$ :

Donnée : $M\left(Zn\right)=65,4g.mo{l}^{-1}$

1. Calculer les quantités de matière $n_0\left(Zn\right)$ et $n_0\left(H_3{O}^{+}\right)$, présentes initialement dans le mélange réactionnel.

2. Recopier, sur votre copie, le tableau d’avancement de la réaction chimique et le compléter.

3. Identifier le réactif limitant. Justifier.

4. Déterminer graphiquement :

a. la valeur du temps de demi-réaction $t_{1/2}$.
b. la valeur de la vitesse volumique de réaction, en unité $(mol.L^{-1}.s^{-1})$, à l’instant $t=400s$, sachant que le volume du mélange réactionnel est $V=40mL$.

5. Interpréter qualitativement la variation de la vitesse volumique de cette réaction.

6) Pour accélérer la réaction précédente, on recommence l’expérience en utilisant la même masse de zinc $m\left(Zn\right)=1,0g$ et le volume $V=40mL$ d’une solution aqueuse $(S’)$ d’acide chlorhydrique de concentration molaire $C_A\text{'}=1mol.L^{-1}$.

• 6.1. Citer le facteur cinétique qui est à l’origine de l’accélération de la réaction.
• 6.2. Le temps de demi-réaction t1/2 va-t-il augmenter ou diminuer ? Justifier.

Partie 2 : Détermination de la constante d’acidité d’un couple (acide/base)

On considère une solution aqueuse d’acide propanoïque $C_2{H}_{5}C{O}_{2}H$ de volume $V$, de concentration molaire $C=2.{10}^{-3}mol.L^{-1}$ et de $pH=3,79$ à $25°C$.

1. Écrire l’équation chimique modélisant la réaction de l’acide propanoïque avec l’eau.

2. Calculer la valeur du taux d’avancement $\tau$ de la réaction. Conclure.

3. Montrer que l’expression de la constante d’acidité $K_{A1}$ du couple $\left(C_2{H}_{5}C{O}_2{H}_{\left(aq\right)}/C_2{H}_{5}C{O}_{2\left(aq\right)}^{-}\right)$ s'écrit $K_{A1}=\frac{{10}^{-2.pH}}{C-{10}^{-pH}}$. Vérifier que $K_{A1}=1,43.{10}^{-5}$

4. Représenter le diagramme de prédominance des deux espèces du couple $\left(C_2{H}_{5}C{O}_2{H}_{\left(aq\right)}/C_2{H}_{5}C{O}_{2\left(aq\right)}^{-}\right)$ présentes dans la solution étudiée.

5) On considère l’acide benzoïque de formule $C_6{H}_{5}C{O}_{2}H$. On note $K_{A2}$ la constante d’acidité du couple $\left(C_6{H}_{5}C{O}_2{H}_{\left(aq\right)}/C_6{H}_{5}C{O}_{2\left(aq\right)}^{-}\right)$. Pour déterminer la valeur de $K_{A2}$, on mélange le même volume de la solution aqueuse d’acide propanoïque et d’une solution aqueuse de benzoate de sodium $C_6{H}_{5}C{O}_{2\left(aq\right)}^{-}+N{a}_{\left(aq\right)}^{+}$. Les deux solutions ont même concentration molaire.

• 5.1. Écrire l’équation chimique de la réaction qui se produit entre l’acide propanoïque $C_2{H}_{5}C{O}_2{H}_{\left(aq\right)}$ et l’ion benzoate $C_6{H}_{5}C{O}_{2\left(aq\right)}^{-}$.
• 5.2. Recopier, sur votre copie, le numéro de la question et écrire la lettre correspondante à la proposition vraie.

L’expression de la constante d’équilibre $K$ associée à l’équation chimique de cette réaction est :

$$\begin{gathered} \overline{)A} K=\frac{K_{A2}}{K_{A1}} ; \overline{)B} K=K_{A1}.K_{A2} \\ \overline{)C} K=\frac{K_{A1}}{K_{A2}} ; \overline{)D} K=\frac{1}{K_{A1}.K_{A2}} \end{gathered}$$

• 5.3. Calculer la valeur de $K_{A2}$ sachant que $K=0,23$.

II- Physique (13 pts)

2-1/ Exercice 1 (3,5 pts) : Propagation des ondes à la surface de l’eau

Les perturbations progressives crées à la surface de l’eau sont des ondes mécaniques. Selon les conditions expérimentales, leur propagation engendre des phénomènes différents. L’étude de ces phénomènes peut fournir des informations sur cette propagation et déterminer certaines de ses caractéristiques.

Cet exercice vise l’étude de la propagation des ondes à la surface de l’eau dans deux situations différentes.

A l’aide d’un vibreur de fréquence réglable, on crée à l’instant $t_0=0$, en un point $S$ de la surface de l’eau d’une cuve à ondes, des ondes progressives sinusoïdales. Ces ondes se propagent sans atténuation et sans réflexion. On règle la fréquence du vibreur sur la valeur $N=50Hz$.

Le document de la figure (1), représente l’aspect de la surface de l’eau à un instant donné :

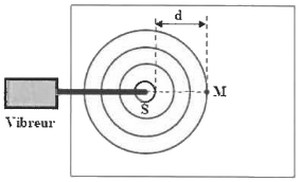
Donnée : $d=15mm$.

1. Définir une onde mécanique progressive.

2) Recopier, sur votre copie, le numéro de la question et écrire la lettre correspondante à la proposition vraie.

• 2.1. La valeur de la longueur d’onde $A$ de l’onde qui se propage à la surface de l’eau est :

$$\begin{gathered} \overline{)A} \lambda =15mm ; \overline{)B} \lambda =7,5mm \\ \overline{)C} \lambda =5mm ; \overline{)D} \lambda =1,5mm \end{gathered}$$

• 2.2. La valeur de la vitesse $v$ de propagation de l’onde à la surface de l’eau est :

$$\begin{gathered} \overline{)A} v=0,75m.s^{-1} ; \overline{)B} v=0,35m.s^{-1} \\ \overline{)C} v=0,25m.s^{-1} ; \overline{)D} v=0,15m.s^{-1} \end{gathered}$$

• 2.3. On considère un point $M$ de la surface de l’eau, tel que $SM=17,5mm$. L’élongation $y_M\left(t\right)$ du point $M$ en fonction de l’élongation $y_S\left(t\right)$ de la source s’écrit :

$$\begin{gathered} \overline{)A} y_M\left(t\right)=y_S\left(t-0,07\right) ; \overline{)B} y_M\left(t\right)=y_S\left(t-0,35\right) \\ \overline{)C} y_M\left(t\right)=y_S\left(t+0,07\right) ; \overline{)D} y_M\left(t\right)=y_S\left(t+0,35\right) \end{gathered}$$

3. On règle la fréquence du vibreur sur la valeur $N\text{'}=100Hz$, la longueur d’onde devient $\lambda \text{'}=3mm$. L’eau est-elle un milieu dispersif ? Justifier.

4) On règle à nouveau la fréquence du vibreur sur la valeur $N=50Hz$ et on place dans l’eau de la cuve un obstacle contenant une ouverture de largeur $a=4,5mm$ (figure 2) :

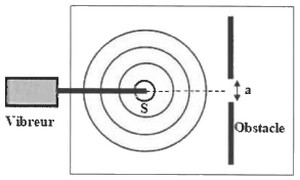
• 4.1. Nommer le phénomène qui se produit. Justifier.
• 4.2. Recopier, sur votre copie, le numéro de la question et écrire la lettre correspondante à la proposition vraie.

Les valeurs de la longueur d’onde et de la vitesse de propagation des ondes à la surface de l’eau lorsque l’onde dépasse l’ouverture sont :

$$\begin{gathered} \overline{)A} \left\{\begin{array}{l}\lambda =3mm\\ v=0,15m.s^{-1}\end{array}\right. ; \overline{)B} \left\{\begin{array}{l}\lambda =15mm\\ v=0,10m.s^{-1}\end{array}\right. \\ \overline{)C} \left\{\begin{array}{l}\lambda =5mm\\ v=0,20m.s^{-1}\end{array}\right. ; \overline{)D} \left\{\begin{array}{l}\lambda =5mm\\ v=0,25m.s^{-1}\end{array}\right. \end{gathered}$$

II- Physique (13 pts)

2-2/ Exercice 2 (3 pts) : Médecine nucléaire

La scintigraphie est une technique d’exploration du corps humain qui permet de diagnostiquer des maladies. Elle consiste à injecter un produit traceur radioactif qui se fixe temporairement sur certains tissus ou organes. Dans le cas de la scintigraphie osseuse, le produit traceur est composé du diphosphonate couplé au technétium métastable, noté ${}^{99}Tc*$ émetteur de rayonnement $\gamma$.

Cet exercice vise l’étude d’une utilisation du technétium en médecine.

Données :

1. Production du technétium ${}^{99}Tc*$

À l’intérieur des générateurs (Molybdène/Technétium), le molybdène ${}_{42}{}^{99}Mo$ se désintègre selon l’équation : ${}_{42}{}^{99}Mo\to {}_{43}{}^{99}Tc*+{}_Z{}^{A}X$

• 1.1. Préciser, en justifiant, le type de cette désintégration.
• 1.2. Déterminer, en unité $MeV$, la valeur de l’énergie libérée $E_{libérée}=\left|\Delta E\right|$, par la désintégration d’un noyau ${}_{42}{}^{99}Mo$.

2. Scintigraphie osseuse à l’aide du technétium

Pour subir une scintigraphie osseuse, une infirmière injecte, à l’instant $t_0=0$, à un patient une dose du produit marqué au technétium ${}^{99}Tc*$. La courbe de la figure ci-dessous représente l’évolution de l’activité de la dose au cours du temps pendant la désintégration du technétium ${}^{99}Tc*$ :

• 2.1. Déterminer graphiquement la valeur de la demi vie $t_{1/2}$ du technétium ${}^{99}Tc*$.
• 2.2. Recopier, sur votre copie, le numéro de la question et écrire la lettre correspondante à la proposition vraie.

La valeur de la constante radioactive $\lambda$ du ${}^{99}Tc*$ vaut :

$$\begin{gathered} \overline{)A} \lambda =0,1155h^{-1} ; \overline{)B} \lambda =1,543.{10}^{-2}{h}^{-1} \\ \overline{)C} \lambda =1,521.{10}^{-2}{h}^{-1} ; \overline{)D} \lambda =2,253.{10}^{-2}{h}^{-1} \end{gathered}$$

• 2.3. Un examen est réalisé trois (3) heures après l’injection de la dose.

Recopier, sur votre copie, le numéro de la question et écrire la lettre correspondante à la proposition vraie.

Le nombre $N$ de noyaux de technétium ${}^{99}Tc*$ au moment de l’examen vaut :

$$\begin{gathered} \overline{)A} N=1,23.{10}^{13} ; \overline{)B} N=4,32.{10}^{13} \\ \overline{)C} N=5,25.{10}^{14} ; \overline{)D} N=7,12.{10}^{14} \end{gathered}$$

• 2.4. Est-il possible de refaire le même examen au patient 48 heures après l’injection de la dose ? Justifier.

II- Physique (13 pts)

2-3/ Exercice 3 (6,5 pts) : Décharge d’un condensateur à travers différents dipôles

La bobine et le condensateur sont deux composants d’une importance capitale dans les circuits électriques. Le fonctionnement de tels circuits dépend du branchement de ces composants, ce qui engendre l’apparition de phénomènes différents. On peut ainsi procéder à l’étude de la charge et la décharge d’un condensateur, de l’établissement ou la rupture du courant, des oscillations électriques libres et des échanges énergétiques dans ces circuits.

Cet exercice vise l’étude de la décharge d’un condensateur à travers un conducteur ohmique, puis à travers une bobine.

On considère le circuit électrique schématisé dans la figure (1), comportant :

• un générateur idéal de force électromotrice $E=6V$.
• un condensateur de capacité C initialement non chargé.
• un interrupteur $K$ à double position;
• un dipôle $D$.

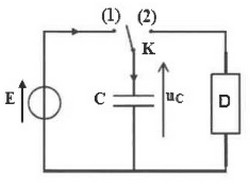
À l'instant $t_0=0$, on place l'interrupteur $K$ en position (1). La charge maximale du condensateur est $Q_0=3\mu C$.

1. Montrer que $C=0,5\mu F$.

2) On réalise trois expériences $\left(1\right)$, $\left(2\right)$ et $\left(3\right)$ en utilisant le dipôle $D$, qui peut être :

• un conducteur ohmique de résistance $R$ (expérience $\left(1\right)$).
• une bobine $b_1\left(L_1;r_1=0\right)$ (expérience $\left(2\right)$).
• une bobine $b_2\left(L_2;r_2=10\Omega \right)$ (expérience $\left(3\right)$).

Pour chaque expérience, on charge totalement le condensateur, puis on le décharge en plaçant l’interrupteur en position $\left(2\right)$ à $t_0=0$.

A l’aide d’un système d’acquisition convenable, on obtient les variations de la tension $u_C\left(t\right)$ aux bornes du condensateur dans le cas des trois expériences :

2.1. Associer chaque courbe à l’expérience qui lui correspond. Justifier.

2.2. Dans le cas de l’expérience $\left(1\right)$, déterminer la valeur de la constante de temps $\tau$ du circuit. Déduire la valeur de $R$.

2.3. Dans le cas de l’expérience $\left(3\right)$ :

• a. Nommer le régime d’oscillations mis en évidence.
• b. Expliquer de point de vue énergétique l’allure de la courbe obtenue.
• c. Déterminer la valeur de la pseudo-période T.

3) Dans le cas de l’expérience (2) :

3.1. Déterminer la valeur de la période propre $T_0$.

3.2. Déterminer la valeur de $L_1$.

3.3. Montrer que l’équation différentielle vérifiée par la charge $q\left(t\right)$ du condensateur s’écrit : $\frac{d^{2}q}{d{t}^2}+\frac{1}{L_1.C}.q=0$

3.4. La solution de l’équation différentielle s’écrit : $q\left(t\right)=Q_m.\cos \left(\frac{2\mathrm{\pi }}{T_0}.t+\phi \right)$

Recopier, sur votre copie, le numéro de la question et écrire la lettre correspondante à la proposition vraie.

• a. L’expression numérique de la charge q en coulomb est :

$$\begin{gathered} \overline{)A} q\left(t\right)=3.{10}^{-6}.\cos \left(500\mathrm{\pi t}\right) ; \overline{)B} q\left(t\right)=0,5.{10}^{-6}.\cos \left(500\mathrm{\pi t}\right) \\ \overline{)C} q\left(t\right)=6.{10}^{-6}.\cos \left(500\mathrm{\pi t}+\frac{\mathrm{\pi }}{2}\right) ; \overline{)D} q\left(t\right)=3.{10}^{-6}.\cos \left(500\mathrm{\pi t}+\mathrm{\pi }\right) \end{gathered}$$

• b. La valeur de l’intensité maximale  du courant électrique qui traverse le circuit est :

$$\begin{gathered} \overline{)A} I_{max}=7,33mA ; \overline{)B} I_{max}=6,85mA \\ \overline{)C} I_{max}=5,22mA ; \overline{)D} I_{max}=4,71mA \end{gathered}$$

3.5. L’énergie totale $\mathcal{E}$ du circuit se conserve. Expliquer pourquoi.

3.6. Calculer la valeur de l’énergie totale $\mathcal{E}$ du circuit.

3.7. Calculer la valeur absolue $\left|q\right|$ de la charge $q\left(t\right)$ du condensateur dans le cas où l’énergie électrique ${\mathcal{E}}_e$ emmagasinée dans le condensateur est égale à l’énergie magnétique ${\mathcal{E}}_m$ emmagasinée dans la bobine.