Séance 17 - Probabilités

Sommaire

I- Terminologie

1-1/ Expérience aléatoire

1-2/ Univers

1-3/ Éventualité

1-4/ Évènement

II- Probabilité sur $\Omega$ l’univers d’une expérience aléatoire

2-1/ Probabilité d’un cas possible à être réalisé

2-2/ Probabilité sur un univers fini (un ensemble fini)

2-3/ Hypothèse d’équiprobabilité

III- Probabilité conditionnelle – Deux événements indépendants - Probabilités composées

3-1/ Probabilité conditionnelle - Deux événements indépendants

3-2/ Probabilité totale

IV- Expérience répétée plusieurs fois

V- Variables aléatoire – loi de probabilité – espérance mathématique – variance – écart-type

5-1/ Variables aléatoire

5-2/ Loi de probabilité d’une variable aléatoire $X$

5-3/ Espérance mathématique - variance – écart-type d’une variable aléatoire $X$

VI- Loi binomiale ou distribution binomiale

VII- Exercices

7-1/ Exercice 1

7-2/ Exercice 2

7-3/ Exercice 3

7-4/ Exercice 4

7-5/ Exercice 5

7-6/ Exercice 6

I- Terminologie

1-1/ Expérience aléatoire

Toute expérience dont ses résultats sont connus mais on ne pas donner le résultat de l’expérience avant de réaliser l’expérience ; on l’appelle expérience aléatoire.

Les résultats obtenues par cette expérience aléatoire on les note par ${\omega }_1$ puis ${\omega }_2$ puis ${\omega }_3$ …… ${\omega }_n$ (en général ${\omega }_i$ avec $i\in \left\{1,2,...,n\right\}$).

Exemple

I- Terminologie

1-2/ Éventualité

Chaque ${\omega }_i$ s’appelle une éventualité ou un événement élémentaire.

Par exemple, lorsqu'on obtient 1, on dit que ${\omega }_1=1$ est une éventualité ou cas possible.

Exemple

I- Terminologie

1-3/ Univers

Les éventualités (ou les événements élémentaires) constituent un ensemble qui s’appelle univers.

Il est noté $\Omega \left({\omega }_1,{\omega }_2,....,{\omega }_n\right)$.

Exemple

I- Terminologie

1-4/ Évènement

Toute partie $A$ de $\Omega$ s’appelle événement.

Par exemple, $A=\left\{PP,FF\right\}\subset \Omega$, donc $A=\left\{PP,FF\right\}$ est un évènement.

On peut exprimer un évènement par une phrase : $A=\left\{PP,FF\right\}$ les deux lancements de dé donnent le même résultat

Si $A=\Omega$ alors l’évènement $\Omega$ s’appelle événement certain.

Si $A=\varnothing$ alors l’évènement $\varnothing$ s’appelle événement impossible.

Si $A=\left\{{\omega }_i\right\}$ alors l’évènement $\left\{{\omega }_i\right\}$ s’appelle événement élémentaire.

Si $A\cap B=\varnothing$ on dit que $A$ et $B$ sont deux événements incompatibles .

Si $A\cap B=\varnothing$ et $A\cup B=\Omega$ alors $B$ s’appelle l’événement contraire de $A$ (et vis versa), on note $B=\overline{A}$ ( de même $A=\overline{B}$).

L’événement $A\cap B$ est l’ensemble constitué par des éventualités réalisées à la fois par les événements $A$ et $B$.

L’événement $A\cup B$ est l’ensemble constitués par des éventualités réalisées soit par l’événement $A$ ou par l’événement $B$.

Les événements $A_1$ et $A_2$ et  ….. $A_p$ est une partition de $\Omega$ s’ils sont disjoints deux à deux et $A_1\cup A_2\cup ...\cup A_p=\Omega$.

Exemple

II- Probabilité sur $\Omega$ l’univers d’une expérience aléatoire

2-1/ Probabilité d’un cas possible à être réalisé

On lance dans l’air une pièce de monnaie 2 fois successives (si le 1er lancer donne P et le 2ème lancer donne F, cette éventualité (ou cas possible) sera notée PF.

Cette expérience est répétée 1000 fois, on obtient les résultats suivants :

• Quel est l’événement élémentaire qui a une grande chance d’être réalisé ?
• Quel est l’événement élémentaire qui a une faible chance d’être réalisé ?

II- Probabilité sur $\Omega$ l’univers d’une expérience aléatoire

2-2/ Probabilité sur un univers fini (un ensemble fini)

Définition

Soit $\Omega =\left({\omega }_1,{\omega }_2,....,{\omega }_n\right)$ l'univers des éventualités d’une expérience aléatoire.

Lorsqu'on répète une expérience aléatoire N fois dans les mêmes conditions, si $n_i$ est le nombre de fois on a obtenu ${\omega }_i$, Le nombre $\frac{n_i}{N}$ s’appelle la probabilité de l’événement élémentaire $\left\{{\omega }_i\right\}$, on note $p_i=p\left(\left\{{\omega }_i\right\}\right)=\frac{n_i}{N}$, et on a $p_1+p_2+p_3+...+p_n=1$.

La probabilité d’un événement A est la somme des probabilités des événements élémentaires qui constituent A, on note $p\left(A\right)$ (exemple : $\Omega =\left\{{\omega }_1,{\omega }_3,{\omega }_6\right\}$ donc $p\left(A\right)=p\left(\left\{{\omega }_1\right\}\right)+p\left(\left\{{\omega }_3\right\}\right)+p\left(\left\{{\omega }_6\right\}\right)$)

Exemple

II- Probabilité sur $\Omega$ l’univers d’une expérience aléatoire

2-2/ Probabilité sur un univers fini (un ensemble fini)

Propriété

A et B sont deux événements d’un univers $\Omega$ d’une expérience aléatoire.

$$\begin{gathered} \forall A\in \Omega ; 0\le p\left(A\right)\le 1 \\ p\left(\Omega \right)=1 \\ p\left(\varnothing \right)=0 \\ p\left(A\cup B\right)=p\left(A\right)+p\left(B\right)-p\left(A\cap B\right) \\ p\left(\overline{A}\right)=1-p\left(A\right) \end{gathered}$$

II- Probabilité sur $\Omega$ l’univers d’une expérience aléatoire

2-3/ Hypothèse d’équiprobabilité

Propriété

Si dans une expérience aléatoire (dont l’univers est $\Omega$), tous les événements élémentaires $A=\left\{{\omega }_i\right\}$ ont la même probabilité (c.à.d. $p\left(\left\{{\omega }_1\right\}\right)=p\left(\left\{{\omega }_2\right\}\right)=...=p\left(\left\{{\omega }_n\right\}\right)$), alors la probabilité d’un évènement A de $\Omega$ est $p\left(A\right)=\frac{cardA}{card\Omega }$.

Remarque

L'équiprobabilité est exprimé par les expressions suivants :

• Des boules indiscernables aux touché.
• On lance un dé (ou une pièce de monnaie) au hasard.

III- Probabilité conditionnelle – Deux événements indépendants - Probabilités composées

3-1/ Probabilité conditionnelle - Deux événements indépendants

Définition

A et B sont deux événements d’un univers $\Omega$ d’une expérience aléatoire.

La probabilité de l’événement B sachons que l’événement A est réalisé est $\frac{p\left(A\cap B\right)}{p\left(A\right)}$, on la note par $p_A\left(B\right)$ ou par $p\left(\raisebox{1ex}{$B$}\!\left/ \!\raisebox{-1ex}{$A$}\right.\right)$.

A et B sont deux événements indépendants si $p\left(A\cap B\right)=p\left(A\right)\times p\left(B\right)$ ou $p_A\left(B\right)=p\left(B\right)$.

$p\left(A\right)\ne 0$ et $p\left(B\right)\ne 0$, l’écriture $p\left(A\cap B\right)=p\left(A\right).p_A\left(B\right)=p\left(B\right).p_B\left(A\right)$ s’appelle la formule de probabilité composée.

Exemple

III- Probabilité conditionnelle – Deux événements indépendants - Probabilités composées

3-2/ Probabilité totale

Définition

$A_1$, $A_2$, $A_3$,....et $A_n$ sont des événements d’un univers $\Omega$ d’une expérience aléatoire qui forment une partition de $\Omega$.

$A_1$, $A_2$, $A_3$,....et $A_n$ sont disjoints 2 à 2 et $A_1\cup A_2\cup A_3\cup ....A_n=\Omega$.

La probabilité d’un événement B de $\Omega$ est :

$p\left(B\right)=p\left(A_1\right)p_{A_1}\left(B\right)+p\left(A_2\right)p_{A_2}\left(B\right)+....+p\left(A_n\right)p_{A_n}\left(B\right)$

Exemple

IV- Expérience répétée plusieurs fois

Propriété

Soit $p=p\left(A\right)$ la probabilité d’un événement A d’un univers $\Omega$ d’une expérience aléatoire.

Soit l’événement C « l’événement A était réalisé k fois après avoir répété cette expérience aléatoire n fois dans les mêmes conditions de départ » avec $k\in \left\{0,1,2,...,n\right\}$.

La probabilité de l’événement C est $p\left(C\right)=C_n^k{p}^k{\left(1-p\right)}^{n-k}$ avec $k\in \left\{0,1,2,...,n\right\}$ et $p=p\left(A\right)$.

Exemple

V- Variables aléatoire – loi de probabilité – espérance mathématique – variance – écart-type

5-1/ Variables aléatoire

On va relier une relation entre l’ensemble des cas possible vers l’ensemble $\mathrm{ℝ}$.

Cette relation notée $X$ est appelée variable aléatoire définie de la manière suivante : $$\begin{gathered} X : \Omega \to \mathrm{ℝ} \\ {\omega }_i\to X\left({\omega }_i\right)=x_i \end{gathered}$$ tel que $x_i$ est le nombre des numéros impaire pour chaque tirage ${\omega }_i$.

Les nombres 0 et 1 et 2 sont appelés les valeurs de la variable aléatoire $X$, on note $x_1=0$ et $x_2=1$ et $x_3=2$, ces nombres constituent un ensemble noté $X\left(\Omega \right)=\left\{0,1,2\right\}$ st appelé ensemble des valeurs de la variable aléatoire $X$, dans le cas général on note $X\left(\Omega \right)=\left\{x_1,x_2,....,x_n\right\}$.

Tous les cas possibles ${\omega }_i$ (les événements élémentaires) qui sont reliés par $x_i$ forment une partie de $\Omega$, cette partie (c’est un événement) sera notée par $\left(X=x_i\right)=\left\{\omega \in \Omega /X\left(\omega \right)=x_i\right\}$.

L’écriture $p\left(X=x_i\right)$ signifie probabilité de l’événement $\left(X=x_i\right)$.

Exemple

V- Variables aléatoire – loi de probabilité – espérance mathématique – variance – écart-type

5-2/ Loi de probabilité d’une variable aléatoire $X$

Définition

Soit $X$ une variable aléatoire définie sur un univers $\Omega$ d’une expérience aléatoire.

L’ensemble des valeurs de $X$ est $X\left(\Omega \right)=\left\{x_1,x_2,....,x_n\right\}$.

Loi de probabilité de $X$ : c’est de calculer toutes les probabilités $p\left(X=x_i\right)$ avec $x_i\in X\left(\Omega \right)$.

On a : $\sum _1^{n}p\left(X=x_i\right)=1$

Exemple

V- Variables aléatoire – loi de probabilité – espérance mathématique – variance – écart-type

5-3/ Espérance mathématique - variance – écart-type d’une variable aléatoire $X$

Définition

Soit $X$ une variable aléatoire définie sur un univers $\Omega$ d’une expérience aléatoire.

L’ensemble des valeurs de $X$ est $X\left(\Omega \right)=\left\{x_1,x_2,....,x_n\right\}$.

Le nombre $\sum _1^n{x}_i.p\left(X=x_i\right)$ s’appelle l’espérance mathématique de la variable aléatoire $X$, on le note $E\left(X\right)$.

Le nombre $E\left(X^2\right)-{\left[E\left(X\right)\right]}^2=\left[\sum _1^n{\left(x_i\right)}^2.p\left(X=x_i\right)\right]-{\left[E\left(X\right)\right]}^2$ s’appelle la variance de la variable aléatoire $X$, on la note $V\left(X\right)$. On a $V\left(X\right)\ge 0$.

Le nombre $\sigma \left(X\right)=\sqrt{V\left(X\right)}$ s’appelle l’écart-type de la variable aléatoire $X$, on le note $\sigma \left(X\right)$.

Exemple

VI- Loi binomiale ou distribution binomiale

Définition et propriété

Soit p est la probabilité de l’événement A d’une expérience aléatoire (seulement une fois).

On répète cette expérience n fois (dans les mêmes conditions de départ).

On considère la variable aléatoire X définie de la manière suivante « le nombre de fois tel que l’évènement A est réalisé après la répétition de l‘expérience de départ n fois »

L'ensemble des valeurs de $X$ est $X\left(\Omega \right)=\left\{0,1,....,n\right\}$.

X est appelé loi binomiale (ou distribution) de paramètres n et p, on la note $X=B\left(n,p\right)$.

Exemple

VII- Exercices

7-1/ Exercice 1

Une urne contient 10 boules : quatre boules rouges et six boules vertes (Les boules sont indiscernables au toucher).

On tire au hasard, simultanément, deux boules de l’urne.

Soit $A$ l’évènement : « Les deux boules tirées sont rouges ».

1. Montrer que $p\left(A\right)=\frac{2}{15}$

Soit $X$ la variable aléatoire qui à chaque tirage associe le nombre de boules rouges restantes dans l’urne après le tirage des deux boules.

2. Montrer que l’ensemble des valeurs prises par $X$ est $\left\{2,3,4\right\}$.

3. Montrer que $p\left(X=3\right)=\frac{8}{15}$ puis déterminer la loi de probabilité de la variable aléatoire $X$.

VII- Exercices

7-2/ Exercice 2

Une urne contient 10 boules portant les nombres 1 ; 2 ; 2 ; 3 ; 3 ; 3 ; 4 ; 4 ; 4 ; 4 (Les boules sont indiscernables au toucher) :

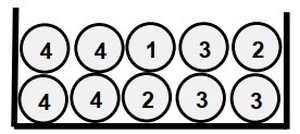
On considère l’expérience suivante : on tire au hasard , successivement et sans remise, deux boules de l’urne.

Soit $A$ l’évènement : "Obtenir deux boules portant deux nombres pairs".

1. Montrer que $p\left(A\right)=\frac{1}{3}$

On répète l’expérience précédente trois fois de suite, en remettant dans l’urne les deux boules tirées après chaque expérience.

Soit $X$ la variable aléatoire égale au nombre de fois où l’évènement $A$ est réalisé.

2. Montrer que $p\left(X=1\right)=\frac{4}{9}$ puis déterminer la loi de probabilité de la variable aléatoire $X$.

VII- Exercices

7-3/ Exercice 3

Une urne contient huit boules indiscernables au toucher portant chacune un nombre comme indiqué sur la figure suivante :

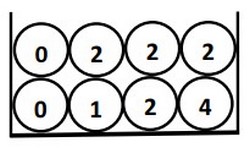
On tire au hasard, simultanément, trois boules de l’urne.

Soit $A$ l’événement : « Parmi les trois boules tirées, aucune boule ne porte le nombre 0 », et $B$ l’événement : « Le produit des nombres portés par les trois boules tirées est égal à 8 »

1. Montrer que $p\left(A\right)=\frac{5}{14}$ et que $p\left(B\right)=\frac{1}{7}$

Soit $X$ la variable aléatoire qui à chaque tirage associe le produit des nombres portés par les trois boules tirées.

2. Montrer que $p\left(X=16\right)=\frac{3}{28}$

Le tableau suivant concerne la loi de probabilité de la variable aléatoire $X$ :

3. Compléter le tableau en justifiant chaque réponse.

VII- Exercices

7-4/ Exercice 4

Une urne contient 10 boules indiscernables au toucher : Cinq boules blanches, trois boules rouges et deux boules vertes :

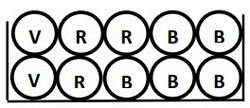
On tire au hasard, simultanément, quatre boules de l’urne.

Soit $A$ l’événement : "Parmi les quatre boules tirées, une seule boule est verte", et $B$ l’événement : "Parmi les quatre boules tirées, il y a exactement trois boules de même couleur".

1. Montrer que $p\left(A\right)=\frac{8}{15}$ et que $p\left(B\right)=\frac{19}{70}$

Soit $X$ la variable aléatoire qui à chaque tirage associe le nombre de boules vertes tirées.

2. Montrer que $p\left(X=2\right)=\frac{2}{15}$

3. Déterminer la loi de probabilité de la variable aléatoire $X$ et montrer que l’espérance mathématique $E\left(X\right)$ est égale à $\frac{4}{5}$.

VII- Exercices

7-5/ Exercice 5

Une caisse contient 3 boules blanches, 4 boules noires et 5 boules rouges. (indiscernables au toucher).

On tire au hasard et simultanément trois boules de la caisse.

On considère les deux événements :

• A: Obtenir trois boules de même couleurs
• B: Obtenir trois boules de couleurs différentes deux à deux

1. Montrer que $P\left(A\right)=\frac{3}{44}$ et $P\left(B\right)=\frac{3}{11}$.

Soit $X$ la variable aléatoire qui à chaque tirage fait correspondre le nombre de couleur des boules tirées.

2. Déterminer les valeurs prises par $X$.

3. Déterminer la loi de probabilité de la variable aléatoire $X$, et calculer l’espérance mathématique $E\left(X\right)$.

VII- Exercices

7-6/ Exercice 6

Une caisse contient dix boules : 5 boules blanches, 3 boules rouges et deux boules noires (indiscernables au toucher).

On tire au hasard et simultanément quatre boules de la caisse.

On considère les deux événements :

• A: Obtenir une seule boule rouge.
• B: Obtenir une boule blanche au moins.

1. Montrer que $P\left(A\right)=\frac{1}{2}$ et $P\left(B\right)=\frac{41}{42}$.

Soit $X$ la variable aléatoire qui à chaque tirage associe le nombre de boules rouges tirées.

2. Vérifier que les valeurs prises par $X$ sont$0 ; 1 ; 2 ; 3$.

3. Montrer que $P\left(X=0\right)=\frac{1}{6}$ et $P\left(X=2\right)=\frac{3}{10}$.

4. Déterminer la loi de probabilité de la variable aléatoire $X$.