
Mathématiques : 2Bac SPC-SVT-Agro-STE-STM
Séance 15 (Géométrie dans l’espace 2 : Produit vectoriel)
Professeur : Mr CHEDDADI Haitam
Sommaire
I- Orientation de l’espace – trièdre – base et repère orientés
1-1/ Trièdre
1-2/ Bonhomme d’Ampère
1-3/ Base et repère orientés
II- Produit vectoriel de deux vecteurs de l’espace orienté
2-1/ Définition géométrique du produit vectoriel
2-2/ Interprétation de la norme du produit vectoriel de deux vecteurs
2-3/ Anti-symétrie et linéarité du produit vectoriel
III- Coordonnées de dans l’espace rapporté à une base orthonormée directe
IV- Distance d’un point à une droite de l’espace
V- Règles du produit vectoriel
VI- Exercices
6-1/ Exercice 1
6-2/ Exercice 2
6-3/ Exercice 3
6-4/ Exercice 4
6-5/ Exercice 5
6-6/ Exercice 6
I- Orientation de l’espace – trièdre – base et repère orientés
1-1/ Trièdre
et et trois demi-droites non coplanaires de l’espace constituent dans cet ordre un trièdre qu'on note
Chaque demi-droite est appelée cote de trièdre.
I- Orientation de l’espace – trièdre – base et repère orientés
1-2/ Bonhomme d’Ampère
est trièdre, on considère une personne virtuel (ou imaginaire) tel que :
ses pieds se trouvent en debout dans le sens de .
il regarde le cote .
On s’intéresse de savoir si oui ou non la main gauche suit le cote .
Cet personne est appelé Bonhomme d’Ampère, donc on a deux positions pour cet personne :
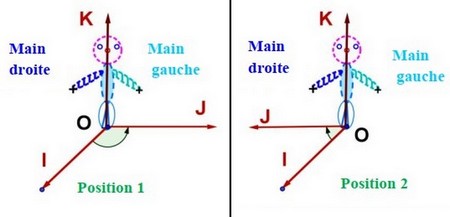
I- Orientation de l’espace – trièdre – base et repère orientés
1-3/ Base et repère orientés
La position du bonhomme d’ampère tel que :
ses pieds se trouvent en debout dans le sens de et il regarde le cote et la main gauche suit le cote ; le trièdre est appelé trièdre directe ou positif, l’autre position le trièdre est appelé trièdre rétrograde ou négative.
On pose : et et , d’où et et sont non coplanaires .
le triplet est une base directe si le trièdre est direct.
Le quadruplet est un repère direct, dans ce cas on dit que l’espace est orienté une orientation directe ou positive.
II- Produit vectoriel de deux vecteurs de l’espace orienté
2-1/ Définition géométrique du produit vectoriel
Définition
Soient et deux vecteurs de l’espace orienté.
Le produit vectoriel de et (dans cet ordre) est le vecteur , on note qui vérifie :
1- Si et sont colinéaires alors .
2- Si et ne sont pas colinéaires alors :
- est orthogonal à et
- est une base directe ou encore est une base directe ou encore est un trièdre direct.
- La norme de est , est la mesure de l’angle géométrique .
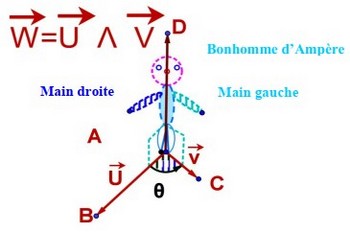
II- Produit vectoriel de deux vecteurs de l’espace orienté
2-1/ Définition géométrique du produit vectoriel
Conséquences
Soient et deux vecteurs de l’espace orienté.
Si et sont non nuls et orthogonaux, alors le triplet est une base orthogonale directe.
Si et sont non nuls et orthogonaux et , alors le triplet est une base orthonormée directe.
Le plan passant par le point a pour vecteurs directeurs et (c.à.d. ) alors le vecteur est normal à ce plan d’où :
( et sont colinéaires).
II- Produit vectoriel de deux vecteurs de l’espace orienté
2-2/ Interprétation de la norme du produit vectoriel de deux vecteurs
La surface du triangle est
La surface du parallélogramme est
II- Produit vectoriel de deux vecteurs de l’espace orienté
2-3/ Anti-symétrie et linéarité du produit vectoriel
et et trois vecteurs de l’espace orienté, et .
L’antisymétrie du produit vectoriel
Bilinéarité du produit vectoriel
III- Coordonnées de dans l’espace rapporté à une base orthonormée directe
Propriété
L’espace rapporté à une base orthonormée directe
Soient et deux vecteurs de l’espace.
On a :
Technique
Exemple
IV- Distance d’un point à une droite de l’espace
Propriété
est une droite passant par le point et est dirigé par un vecteur directeur de l’espace.
est un point de l’espace.
La distance du point à la droite est :
Exemple
V- Règles du produit vectoriel
Règle du tire bouchon
Règle de la main droite
Bonhomme d’Ampère
VI- Exercices
6-1/ Exercice 1
Dans l’espace rapporté à un repère orthonormé direct , on considère les points , , et la sphère d’équation :
- Montrer que
- En déduire que est une équation cartésienne du plan .
- Montrer que la sphère a pour centre le point et pour rayon .
- Montrer que , et en déduire que le plan coupe la sphère suivant un cercle .
- Déterminer une représentation paramétrique de la droite passant par le point et orthogonale au plan .
- Montrer que le point B est le centre du cercle .
VI- Exercices
6-2/ Exercice 2
Dans l’espace rapporté à un repère orthonormé direct , on considère le plan passant par le point et dont est un vecteur normal et la sphère de centre le point et de rayon .
- Montrer que est une équation cartésienne du plan .
- Montrer que le plan est tangent à la sphère et vérifier que est le point de contact.
- Déterminer une représentation paramétrique de la droite passant par le point et orthogonale au plan .
- Montrer que la droite est tangente à la sphère au point .
- Montrer que et en déduire l’aire du triangle .
VI- Exercices
6-3/ Exercice 3
L’espace est rapporté à un repère orthonormé direct .
On considère la sphère d’équation et le plan d’équation .
- Montrer que la sphère a pour centre le point et pour rayon .
- Calculer et en déduire que le plan coupe la sphère suivant un cercle .
- Déterminer le centre et le rayon du cercle .
Soit la droite passant par le point et orthogonale au plan .
- Montrer que est un vecteur directeur de la droite .
- Montrer que et en déduire que la droite coupe la sphère en deux points.
- Déterminer les coordonnées de chaque point d’intersection de la droite et de la sphère .
VI- Exercices
6-4/ Exercice 4
Dans l’espace rapporté à un repère orthonormé direct , on considère les points , et .
- Montrer que et en déduire que est une équation cartésienne du plan .
On considère la sphère dont une équation est .
- Vérifier que la sphère a pour centre et pour rayon .
- Vérifier que est une représentation paramétrique de la droite passant par le point et orthogonale au plan .
- Déterminer les coordonnées de point d’intersection de la droite et du plan .
- Vérifier que , puis montrer que le plan coupe la sphère selon un cercle de rayon , dont on déterminera le centre.
VI- Exercices
6-5/ Exercice 5
L’espace est rapporté à un repère orthonormé direct .
On considère les points , , et .
Soit l’ensemble des points vérifiant .
- Déterminer les coordonnées , et en déduire que est une équation cartésienne du plan .
- Vérifier que est la sphère de centre et de rayon .
- Calculer la distance de au plan .
- En déduire que le plan est tangent à la sphère .
- Vérifier que , et en déduire que est le point contact de la sphère et du plan .
VI- Exercices
6-6/ Exercice 6
L’espace est rapporté à un repère orthonormé direct .
On considère les points , et .
Soit la sphère d’équation :
- Montrer que , et en déduire que est une équation cartésienne du plan .
- Montrer que est la sphère de centre et de rayon .
Soit la droite passant par et perpendiculaire au plan .
- Montrer que est une représentation paramétrique de la droite .
- Montrer que la droite coupe la sphère aux deux points et .


