
Physique et Chimie : 2ème Bac SM-SPC
Séance 19-B (Mouvements plans : Particule chargée dans un champ magnétique)
Professeur : Mr EL GOUFIFA Jihad
Sommaire
I- Mouvement d'une particule chargée dans un champs magnétique uniforme
1-1/ Le champ magnétique uniforme
1-2/ Déviation d'une particule chargée dans un champ magnétique uniforme
1-3/ La force magnétique (force de Lorentz)
1-4/ Étude du mouvement d'une particule chargée dans un champ magnétique uniforme
1-5/ La déviation magnétique
II- Exercices
2-1/ Exercice 1
2-2/ Exercice 2
2-3/ Exercice 3
2-4/ Exercice 4
I- Mouvement d'une particule chargée dans un champs magnétique uniforme
1-1/ Le champ magnétique uniforme
Un champ magnétique est dit uniforme s'il est constant en direction, en sens et en valeur.
- Exemple : Le champ magnétique est uniforme entre les bobines d'Helmholtz parcourues par un courant électrique :

L'unité de l'intensité du champ magnétique est le tesla (T).
Remarque
Si le vecteur →B est perpendiculaire au plan de la feuille et dirigée vers l'avant on le représente par : ⊙→B
Si le vecteur →B est perpendiculaire au plan de la feuille et dirigée vers l'arrière on le représente par : ⊗→B
I- Mouvement d'une particule chargée dans un champs magnétique uniforme
1-2/ Déviation d'une particule chargée dans un champ magnétique uniforme
Expérience
On utilise un tube de crookes (qui contient un canon d'électrons permettant d'obtenir un faisceau d'électrons ayant la même vitesse), à l'intérieur duquel il y'a un champ magnétique uniforme entre deux bobines d'Helmholtz parcourues par un courant électrique :
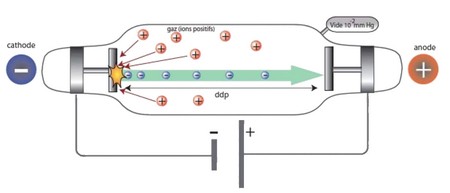
On constate expérimentalement que :
Si la vitesse des électrons →v0 est parallèle à →B, le faisceau d'électrons ne subit pas de déviation.
Si la vitesse des électrons →v0 est perpendiculaire à →B, le faisceau d'électrons dévie et sa trajectoire devient circulaire.

I- Mouvement d'une particule chargée dans un champs magnétique uniforme
1-2/ Déviation d'une particule chargée dans un champ magnétique uniforme
Interprétation
La déviation du faisceau d'électron est due à l'existence d'une force magnétique qui s'exerce sur toute particule chargée et en mouvement dans un champ magnétique uniforme qu'on appelle : force magnétique ou force de Lorentz.
I- Mouvement d'une particule chargée dans un champs magnétique uniforme
1-3/ La force magnétique (force de Lorentz)
Définition
Toute particule chargée de vitesse est soumise dans un champ magnétique uniforme à une force magnétique appelée force de Lorentz donnée par la relation suivante :
→F=q.→v∧→B
Le symbole ∧ signifie produit vectoriel.
Caractéristiques de la force magnétique
L'intensité : F=|q|.v.B.sin(^→B,→v)
La direction : la force magnétique.
Le sens : il est donné par la règle de la main droite suivante :
En plaçant la main droite tendue de sorte que les doigts soient dirigés dans le sens du produit q.→v et la paume de la main soit dirigée dans le sens de →B, le pouce tendu indique le sens de la force magnétique :
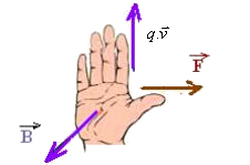
Exemples
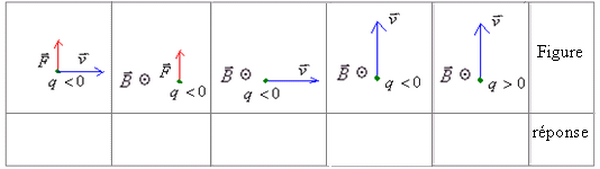
I- Mouvement d'une particule chargée dans un champs magnétique uniforme
1-4/ Étude du mouvement d'une particule chargée dans un champ magnétique uniforme
Mouvement uniforme
L'électron dans le champ magnétique est soumis à l'action de la force magnétique →F=q.→v∧→B, cette force de Lorentz est toujours perpendiculaire au vecteur vitesse →v.
Donc le produit scalaire →F.→v=0
Par conséquence la puissance de la force magnétique est nulle P=→F.→v=0,donc son travail est nulW→F=0 .
En appliquant le théorème de l'énergie cinétique : ΔEc=W→F=0⇒Eci=Ecf
Donc sa vitesse est constante v= Cte.
Donc l'action du champ magnétique ne modifie pas l'énergie cinétique de la particule.
I- Mouvement d'une particule chargée dans un champs magnétique uniforme
1-4/ Étude du mouvement d'une particule chargée dans un champ magnétique uniforme
Mouvement plan
La vitesse de l’électron est constante v= Cte.
Donc son accélération tangentielle at=dvdt=0 est nulle.
Alors l'accélération de l'électron est normale.
Et on a →F=q.→v∧→B
Donc la force magnétique →F est perpendiculaire au plan (→B,→v), est elle aussi normale.
En conclusion, le mouvement de l'électron est plan, il se fait dans un plan perpendiculaire au vecteur champ magnétique.
I- Mouvement d'une particule chargée dans un champs magnétique uniforme
1-4/ Étude du mouvement d'une particule chargée dans un champ magnétique uniforme
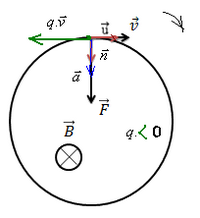
Mouvement circulaire
Dans le repère de Frenet, le vecteur accélération : →a=an→n+at→u
or :v=Cte⇒at=dvdt=0
Donc l'accélération est normale.
En appliquant la deuxième loi de Newton : →F=q.→v∧→B=m→aG
En projetant sur la normale : →F=|q|v.B=mv2R⇒R=mv|q|.B
Le rayon est constant donc le mouvement est circulaire.
I- Mouvement d'une particule chargée dans un champs magnétique uniforme
1-5/ La déviation magnétique
On fait pénétrer un faisceau d'électron dans une région de l'espace de largeur l dans laquelle règne un champ magnétique →B uniforme avec une vitesse →v0, le faisceau d’électrons est soumis à l'action de la force magnétique et son mouvement devient circulaire de rayon R=mv0|q|.B dans le champ magnétique.
Les électron du faisceau quittent le champ magnétique au point S et prennent un mouvement rectiligne uniforme jusqu'à ce qu'ils rencontrent l'écran au point P.
On appelle déviation magnétique la distance Dm=O'P

{sinα=lR (HM'I)tanα=DmD (JPO')tanα≈sinα⇒DmD=lR⇒Dm=DlR=Dl|q|Bmv0
II- Exercices
2-1/ Exercice 1
Les ions Mg2+ pénètrent dans une région de l’espace où règne un champ magnétique uniforme →B (perpendiculaire au plan de la figure). Avec une vitesse V0=1,6.104m.s-1
- Donner les caractéristique de la force magnétique →Fm
- Déterminer le sens du champs magnétique →B
- En appliquant la deuxième loi de newton dans un référentiel galiléen, montrer que le mouvement des ions Mg2+ est circulaire uniforme
- Calcule la masse d’ion Mg2+ (On donne OM=4cm)
Données :
- L’intensité du champs magnétique B=0,1T
- La charge élémentaire e=1,6.10-19C
II- Exercices
2-2/ Exercice 2
On considère les ions de deux isotopes H20080g2+ et H20280g2+ du mercure.
Ils pénètrent en A, avec une vitesse V non nulle, dans une capsule où règne un champ magnétique uniforme (perpendiculaire au plan de la feuille) :
- Indiquer le sens du champ magnétique pour que les ions soient déviés vers le détecteur D.
- Montrer que dans cette capsule les ions ont un mouvement uniforme, et exprimer les rayons R de la trajectoire de deux isotopes en fonction de m, e, v et B.
- Déterminer lequel de ces deux ions va être le plus dévié. Justifier.
II- Exercices
2-3/ Exercice 3
Deux particules chargées He2+ et O2- sont introduites en un point A, avec la même vitesse initiale →V, dans un espace où règne un champ magnétique uniforme →B perpendiculaire au vecteur →V.
On considère que les deux particules He2+ et O2- ne sont soumises qu’à la force de Lorentz.
Données :
L’expression de la force de Lorentz : →F=q→V∧→B
La masse de la particule He2+ : m(He2+)=6,68.10-27Kg
La figure suivante représente l’enregistrement des deux trajectoires des particules He2+ et O2- dans le champ magnétique uniforme →B :
- Identifier la trajectoire correspondante à chaque particule.
- En appliquant la deuxième loi de Newton dans un référentiel galiléen, montrer que le mouvement de l’ion He2+ est uniforme et de trajectoire circulaire de rayon RHe2+=mHe2+.V2.e.B
- En exploitant la figure, déterminer le rapport RO2-RHe2+
- Montrer que la masse de la particule O2- est m(O2-)=2,67.10-26Kg


