Séance 9 - Triangles isométriques et triangles semblables

Sommaire

I- Triangles isométriques

1-1/ Définition

1-2/ Remarques

1-3/ Propriété

1-4/ Cas d’isométrie

II- Triangles semblables

2-1/ Définition

2-2/ Remarques

2-3/ Propriété

2-4/ Cas de similitude

III- Exercices

3-1/ Exercice 1

3-2/ Exercice 2

3-3/ Exercice 3

3-4/ Exercice 4

3-5/ Exercice 5

3-6/ Exercice 6

I- Triangles isométriques

1-1/ Définition

Deux triangles isométriques sont des triangles superposables.

Exemple

Soient $ABC$ et $EFG$ deux triangles isométriques.

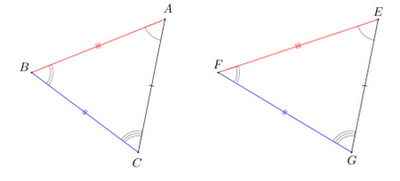
I- Triangles isométriques

1-2/ Remarques

Les côtés $\left[AB\right]$ et $\left[EF\right]$ sont appelés côtés correspondants.

De même: $\left[AC\right]$ et $\left[EG\right]$ ; $\left[BC\right]$ et $\left[FG\right]$.

Les angles $\widehat{ABC}$ et $\widehat{EFG}$ sont appelés angles correspondants.

De même: $\widehat{ACB}$ et $\widehat{EGF}$ ; $\widehat{BAC}$ et $\widehat{FEG}$.

I- Triangles isométriques

1-3/ Propriété

Si deux triangles sont isométriques, alors :

• Leurs côtés correspondants sont de même longueur.
• Leurs angles correspondants sont de même mesure.

I- Triangles isométriques

1-4/ Cas d’isométrie

Premier cas

Si deux triangles ont leurs côtés respectivement de même longueur, alors les deux triangles sont isométriques.

Exemple

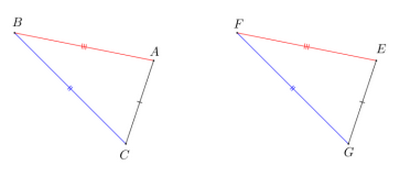
$ABC$ et $EFG$ sont deux triangles isométriques car :

$$\begin{gathered} AB=EF \\ AC=EG \\ BC=FG \end{gathered}$$

I- Triangles isométriques

1-4/ Cas d’isométrie

Second cas

Si deux triangles ont un angle de même mesure compris entre deux côtés respectivement de même longueur, alors les deux triangles sont isométriques.

Exemple

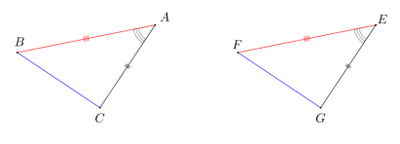
$ABC$ et $EFG$ sont deux triangles isométriques car :

$$\begin{gathered} AB=EF \\ AC=EG \\ \widehat{BAC}=\widehat{FEG} \end{gathered}$$

I- Triangles isométriques

1-4/ Cas d’isométrie

Troisième cas

Si deux triangles ont un côté de même longueur adjacent à deux angles de même mesure, alors les deux triangles sont isométriques.

Exemple

$ABC$ et $EFG$ sont deux triangles isométriques car :

$$\begin{gathered} AB=EF \\ \widehat{ABC}=\widehat{EFG} \\ \widehat{BAC}=\widehat{FEG} \end{gathered}$$

II- Triangles semblables

2-1/ Définition

Deux triangles semblables sont des triangles qui ont leurs angles deux à deux de même mesures.

Exemple

On considère les triangles $ABC$ et $EFG$ tels que  $\widehat{ABC}=\widehat{EFG}$ et $\widehat{ACB}=\widehat{EGF}$ et $\widehat{BAC}=\widehat{FEG}$ :

On dit que les triangles $ABC$ et $EFG$ sont semblables.

II- Triangles semblables

2-2/ Remarques

Les côtés $\left[AB\right]$ et $\left[EF\right]$ sont appelés côtés correspondants.

De même: $\left[AC\right]$ et $\left[EG\right]$ ; $\left[BC\right]$ et $\left[FG\right]$.

Les angles $\widehat{ABC}$ et $\widehat{EFG}$ sont appelés angles correspondants.

De même: $\widehat{ACB}$ et $\widehat{EGF}$ ; $\widehat{BAC}$ et $\widehat{FEG}$.

II- Triangles semblables

2-3/ Propriété

Si deux triangles sont semblables, alors les longueurs de leurs côtés correspondants sont proportionnelles.

Autrement dit

Si $ABC$ et $EFG$ sont deux triangles semblables (dans cet ordre), alors :

$\frac{AB}{EF}=\frac{AC}{EG}=\frac{BC}{FG}=k$

$k$ est appelé rapport de similitude.

Exemple

II- Triangles semblables

2-4/ Cas de similitude

Premier cas

Si deux triangles ont deux angles qui ont même mesure, alors les triangles sont semblables.

Exemple

II- Triangles semblables

2-4/ Cas de similitude

Second cas

Si deux triangles ont un angle de même mesure compris entre deux côtés dont les longueurs sont respectivement proportionnelles, alors les triangles sont semblables.

Autrement dit

Soient $ABC$ et $EFG$ deux triangles.

Si $\left\{\begin{array}{l}\widehat{BAC}=\widehat{FEG}\\ \frac{AB}{EF}=\frac{AC}{EG}\end{array}\right.$, alors les triangles $ABC$ et $EFG$ sont semblables.

Exemple

II- Triangles semblables

2-4/ Cas de similitude

Troisième cas

Si deux triangles ont les longueurs de leur côtés respectivement proportionnelles, alors les triangles sont semblables.

Autrement dit

Soient $ABC$ et $EFG$ deux triangles.

Si $\frac{AB}{EF}=\frac{AC}{EG}=\frac{BC}{FG}$, alors les triangles $ABC$ et $EFG$ sont semblables.

Exemple

III- Exercices

3-1/ Exercice 1

On considère la figure suivante :

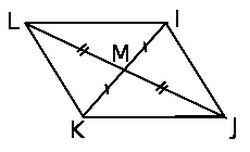
$ILJK$ est un parallélogramme de centre $M$.

1. Montrer que les deux triangles $LKJ$ et $IJL$ sont isométriques.

2. Montrer que les deux triangles $LMK$ et $IJM$ sont isométriques.

III- Exercices

3-2/ Exercice 2

On considère la figure suivante :

$ABC$ est un triangle isocèle en $A$ et $\left[AD\right)$ est la bissectrice de l’angle $\widehat{BAC}$.

1. Prouver que les triangles $ABI$ et $ACI$ sont isométriques.

2. Prouver que $\widehat{DAC}$ et $\widehat{ICD}$.

3. Montrer que les triangles $ADC$ et $ICD$ sont semblables.

4. Montrer que : $AD x CI = AC x CD$.

III- Exercices

3-3/ Exercice 3

On considère la figure suivante :

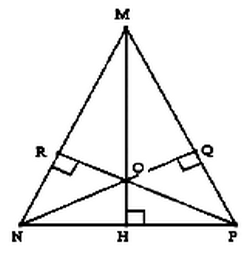
$MNP$ est un triangle isocèle de sommet $M$.

1. Prouver que les deux triangles $OMN$ et $OMP$ sont isométriques.

2. Montrer que les deux triangles $MOQ$ et $MNH$ sont semblables.

3. En déduire que :$MO \times MH = MN \times MQ$.

III- Exercices

3-4/ Exercice 4

$ABCD$ est un parallélogramme, $N$ un point du segment $\left[DC\right]$ distinct de $D$ et $C$.

La droite $\left(AN\right)$ coupe $\left(BC\right)$ en $M$.

1. Démontrer que les triangles $ADN$ et $ABM$ sont des triangles semblables.

2. En déduire que $DN \times BM = AB \times AD$.

III- Exercices

3-5/ Exercice 5

$ABCD$ est un quadrilatère convexe inscrit dans un cercle tel que $\left[AC\right]$ est un diamètre.

Soit $H$ le projeté orthogonal du point $A$ sur la droite $\left(DB\right)$.

1. Comparer les deux triangles $AHB$ et $ADC$.

2. Montrer que : $AD\times AB=AC\times AH$

III- Exercices

3-6/ Exercice 6

$\left(C\right)$ est un cercle et $A$ un point extérieur à $\left(C\right)$.

Du point $A$, on construit deux droites $\left(\Delta \right)$ et $\left(\Delta \text{'}\right)$ tels que la droite $\left(\Delta \right)$ coupe $\left(C\right)$ en $E$ et $F$, et la droite $\left(\Delta \text{'}\right)$ coupe $\left(C\right)$ en $B$ et $C$.

1. Comparer les triangles $ABF$ et $AEC$.

2. Démontrer que $\widehat{AEC}=\widehat{FBA}$.

3. Démontrer que $AE\times AF=AB\times AC$.