
Mathématiques : 2Bac Eco-SGC
Séance 5 (Étude d’une fonction numérique)
Professeur : Mr ETTOUHAMY Abdelhak
Sommaire
I- Étude des branches infinies (Rappel)
1-1/ Les asymptotes
1-2/ Les branches paraboliques
II- Axe de symétrie – Centre de symétrie
2-1/ Proposition 1
2-2/ Proposition 2
III- Exercices
3-1/ Exercice 1 (Étude d’une fonction polynôme)
3-2/ Exercice 2 (Étude d’une fonction rationnelle)
3-3/ Exercice 3 (Étude d’une fonction irrationnelle)
3-4/ Exercice 4
I- Étude des branches infinies (Rappel)
1-1/ Les asymptotes
Dans tout ce qui suit, f est une fonction numérique de la variable réelle x et (Cf) sa représentation graphique dans un repère orthonormé (O,→i,→j)
L’asymptote horizontale
La droite d’équation y=b est une asymptote horizontale de la courbe (Cf) si et seulement si limx→±∞f(x)=b

Exemple
I- Étude des branches infinies (Rappel)
1-1/ Les asymptotes
L’asymptote verticale
La droite d’équation x=a est une asymptote verticale de la courbe (Cf) si et seulement si limx→af(x)=±∞
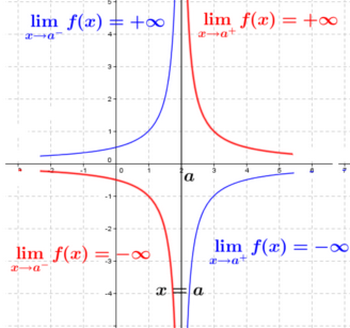
Exemple
I- Étude des branches infinies (Rappel)
1-1/ Les asymptotes
L’asymptote oblique
La droite d’équation y=ax+b est une asymptote oblique de la courbe (Cf) si et seulement si limx→∞f(x)x=a (a≠0) et limx→∞f(x)-ax=b
La droite d’équation y=ax+b est une asymptote oblique de la courbe (Cf) si et seulement si limx→∞f(x)-(ax+b)=0

Exemple
I- Étude des branches infinies (Rappel)
1-2/ Les branches paraboliques
Branche parabolique dirigée vers l’axe des ordonnées
Si limx→±∞f(x)=±∞ et limx→±∞f(x)x=±∞ on dit que la courbe (Cf) admet une branche parabolique dirigée vers l’axe des ordonnées.

Exemple
I- Étude des branches infinies (Rappel)
1-2/ Les branches paraboliques
Branche parabolique dirigée vers l’axe des abscisses
Si limx→±∞f(x)=±∞ et limx→±∞f(x)x=0 on dit que la courbe (Cf) admet une branche parabolique dirigée vers l’axe des abscisses.
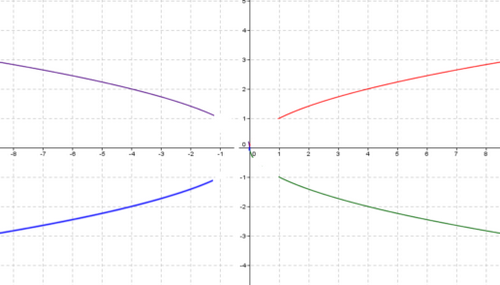
Exemple
I- Étude des branches infinies (Rappel)
1-2/ Les branches paraboliques
Branche parabolique de direction la droite d’équation y=ax
Si limx→±∞f(x)x=a (a≠0) et limx→±∞f(x)-ax=±∞ on dit que la courbe (Cf) admet une branche parabolique de direction la droite d’équation y=ax
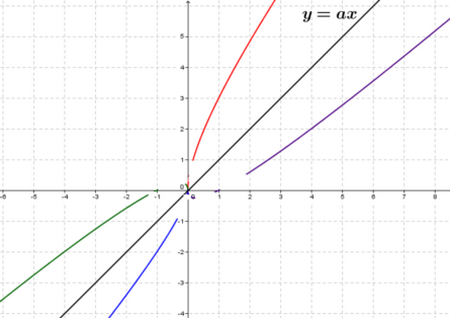
Exemple
II- Axe de symétrie – Centre de symétrie
2-1/ Proposition 1
Soit f une fonction numérique et (Cf) sa courbe représentative dans un repère orthogonal.
Pour que la droite (D) d’équation x=a soit un axe de symétrie de la courbe (Cf), il suffit de montrer que pour toutx∈Df : (2a-x)∈Df et f(2a-x)=f(x)
Exemple
II- Axe de symétrie – Centre de symétrie
2-2/ Proposition 2
Soit f une fonction numérique et (Cf) sa courbe représentative dans un repère orthogonal.
Pour que le point Ω(a,b) soit un centre de symétrie de la courbe (Cf), il suffit de montrer que pour tout x∈Df : (2a-x)∈Df et f(2a-x)=2b-f(x)
Exemple
III- Exercices
3-1/ Exercice 1 (Étude d’une fonction polynôme)
f est la fonction définie par f(x)=x4-2x2
- Donner le domaine de définition de la fonction f
- Calculer limx→+∞f(x) et limx→-∞f(x)
- Étudier le comportement de la fonction f au voisinage de +∞ et -∞
- Donner le tableau de variation de la fonction f
- Déterminer les extremums de f
- Déterminer les points d’inflexions de la courbe représentant la fonction f
- Déterminer les points d’intersection de la courbe représentant la fonction f et (ox)
- Tracer la courbe représentant la fonction f dans un repère orthonormé
III- Exercices
3-2/ Exercice 2 (Étude d’une fonction rationnelle)
f est la fonction définie par f(x)=x2+x+32x2+2x-4
- Donner le domaine de définition de la fonction f
- Calculer les limites de la fonction f aux bornes de son domaine de définition et donner l’interprétation graphique des résultats obtenus
- Donner le tableau de variation de la fonction f
- Tracer la courbe représentant la fonction f dans un repère orthonormé
- Montrer que la droite d’équation x=-12 est un axe de symétrie de la courbe représentant la fonction f
III- Exercices
3-3/ Exercice 3 (Étude d’une fonction irrationnelle)
f est la fonction définie par f(x)=√x2-4
- Donner le domaine de définition de la fonction f
- Calculer limx→+∞f(x) et limx→-∞f(x)
- Étudier la dérivabilité de f à droite de 2 et à gauche de -2
- Donner une interprétation géométrique des résultats de la question 3
- Calculer la dérivée de la fonction f et étudier son signe
- Donner le tableau de variation de la fonction f
- Étudier les branches infinies de la courbe (Cf) représentant la fonction f.
- Tracer la courbe (Cf) représentant la fonction f
III- Exercices
3-4/ Exercice 4
- Étudier la convexité de la courbe représentative de la fonction f et déterminer les points d'inflexion (s'ils existent ) dans les cas suivants :
1 f(x)=√2x-2+x2 f(x)=13x3+32x2-4x+13 f(x)=(x-1)√x-1


