Séance 2 - Continuité (Partie 1)

Sommaire

I- Continuité en un point et continuité sur un intervalle

1-1/ Continuité en un point

1-2/ Continuité à droite – Continuité à gauche

1-3/ Continuité sur un intervalle

1-4/ Les opérations sur les fonctions continues

II- Image d’un intervalle par une fonction continue

2-1/ Image d‘un intervalle

2-2/ Cas d’une fonction continue et strictement monotone

III- Exercices

3-1/ Exercice 1

3-2/ Exercice 2

3-3/ Exercice 3

3-4/ Exercice 4

3-5/ Exercice 5

3-6/ Exercice 6

I- Continuité en un point et continuité sur un intervalle

1-1/ Continuité en un point

Définition

Soit $f$ une fonction définie sur un intervalle $I$ et $a$ un élément de $I$

$f$ est continue en $a$, si $\underset{x\to a}{\lim }f\left(x\right)=f\left(a\right)$

Exemples

I- Continuité en un point et continuité sur un intervalle

1-1/ Continuité en un point

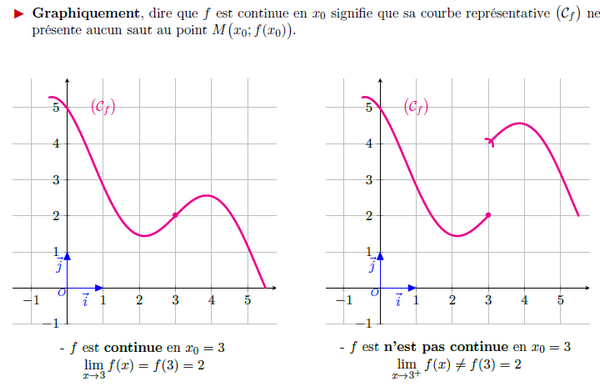
I- Continuité en un point et continuité sur un intervalle

1-2/ Continuité à droite – Continuité à gauche

Définition

- Soit $f$ une fonction définie sur un intervalle de type  $[a;a+\alpha [$ avec $\alpha >0$ , alors 

$f$ est continueà droite en $a$, si $\underset{x\to a^{+}}{\lim }f\left(x\right)=f\left(a\right)$

- Soit $f$ une fonction définie sur un intervalle de type  $]a-\alpha ;a]$ avec $\alpha >0$ , alors 

$f$ est continue à gauche  en  $a$, si $\underset{x\to a^{+}}{\lim }f\left(x\right)=f\left(a\right)$

Exemple

I- Continuité en un point et continuité sur un intervalle

1-2/ Continuité à droite – Continuité à gauche

Propriété

Soit $f$ une fonction numérique  définie sur un intervalle ouvert $I$ et $a\in I$.

La fonction $f$ est continue en $a$ si et seulement si $f$ est continue à droite et à gauche en $a$.

c-à-d : $$\begin{gathered} \overline{) \\ \underset{x\to a^{-}}{\lim }f\left(x\right)=\underset{x\to a^{+}}{\lim }f\left(x\right)=f\left(a\right)} \end{gathered}$$

Exemple

I- Continuité en un point et continuité sur un intervalle

1-3/ Continuité sur un intervalle

Définition

$f$ est continue sur un intervalle ouvert $]a,b[$ si $f$ est continue en tous points de cet intervalle

$f$ est continue sur un intervalle fermé $\left[a,b\right]$ si $f$ est continue sur l’intervalle ouvert $]a,b[$ et continue à droite en $a$, et à gauche en $b$.

I- Continuité en un point et continuité sur un intervalle

1-3/ Continuité sur un intervalle

Propriétés

Les fonctions polynômes sont continue sur $\mathrm{ℝ}$.

Les fonctions rationnelles sont continues sur chaque intervalle de leur ensemble de définition.

La fonction $x\mapsto \sqrt{x}$ est continue sur $[0,+\infty [$

Exemples

I- Continuité en un point et continuité sur un intervalle

1-3/ Continuité sur un intervalle

Remarque

- Graphiquement, une fonction est continue sur un intervalle, si on peut tracer son graphe sans lever le crayon sur cet intervalle

- Toute fonction continue sur un intervalle I, sa restriction est continue sur tout intervalle inclus dans I.

Exemple

I- Continuité en un point et continuité sur un intervalle

1-4/ Les opérations sur les fonctions continues

propriétés

Soient $f$ et $g$ deux fonctions continues sur un intervalle $I$ et $k\in \mathrm{ℝ}$

- Les fonctions $\left(f+g\right)$ et $\left(f.g\right)$ et $\left(k.f\right)$ sont continus sur $I$

- Si $g$ ne s’annule pas sur $I$, alors $\frac{1}{g}$ et $\frac{f}{g}$ sont continués sur $I$

- Si la fonction $f$ est continue et positive sur un intervalle $I$, alors la fonction $\sqrt{f}$ est continue sur $I$.

Exemples

II- Image d’un intervalle par une fonction continue

2-1/ Image d‘un intervalle

Propriété

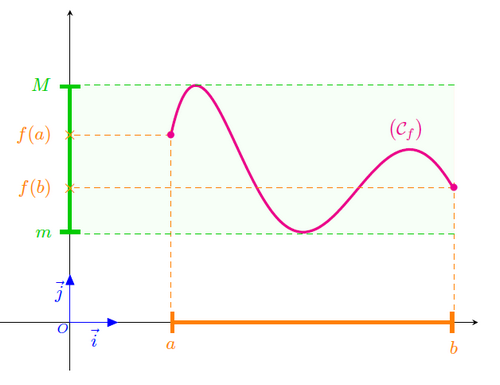
- Si $f$ une fonction numérique continue sur un intervalle $I$, alors son image par $f$ est un intervalle.

- Si $f$ une fonction numérique  continue sur un segment $\left[a;b\right]$, alors son image par $f$ est un segment $\left[m;M\right]$,

         où $m$ et $M$ sont, respectivements, les valeurs minimale et maximale de $f$ sur le segment $\left[a;b\right]$.

Géométriquement

Exemple :

II- Image d’un intervalle par une fonction continue

2-2/ Cas d’une fonction continue et strictement monotone

Si $f$ est une fonction strictement croissante :

Si $f$ est une fonction strictement décroissante :

Exemple

III- Exercices

3-1/ Exercice 1

Étudier la continuité de $f$ en $a$ dans chaque cas :

A- $\left\{\begin{array}{l}f\left(x\right)=\frac{x^2-1}{x+1} ; x\ne -1\\ f\left(-1\right)=0\end{array}\right.; a=-1$

B- $\left\{\begin{array}{l}f\left(x\right)=\frac{\sqrt{3x+1}-2}{x-1} ; x\ne 1\\ f\left(1\right)=-\frac{1}{4}\end{array}\right.; a=1$

C- $\left\{\begin{array}{l}f\left(x\right)=\frac{\sqrt{x+3}-2}{x^2+x-2} ; x\ne 1\\ f\left(1\right)=\frac{1}{12}\end{array}\right.; a=1$

III- Exercices

3-2/ Exercice 2

A- Soit $f$ la fonction définie sur $\mathrm{ℝ}$ par :

$\left\{\begin{array}{l}f\left(x\right)=2+\sqrt{5-x} ; x\le 4\\ f\left(x\right)=\frac{x-4}{\sqrt{x}-2} ; x>4\end{array}\right.$

1. Étudier la continuité de $f$ à gauche et à droite en 4

2. Est-ce que $f$ est continue en 4 ?

B- Soit $g$ la fonction définie sur $\mathrm{ℝ}$ par :

$\left(\begin{array}{c}g\left(x\right)=\frac{x}{\sqrt{x}} ; x>0\\ g\left(x\right)=\frac{\sqrt{x^2+1}-1}{x} ; x<0\\ g\left(0\right)=0\end{array}\right)$

1. Étudier la continuité de $g$ en 0

III- Exercices

3-3/ Exercice 3

A- Soit $f$ la fonction définie sur $\mathrm{ℝ}$ par :

$\left\{\begin{array}{l}f\left(x\right)=x^3+2x ; x\le 1\\ f\left(x\right)=\frac{x^2+x-2}{x-1} ; x>1\end{array}\right.$

1. Étudier la continuité de $f$ en 1
2. Étudier la continuité de $f$ sur $]-\infty ;1[$ et $]1;+\infty [$
3. Est-ce que $f$ est continue sur $\mathrm{ℝ}$ ?

B- Soit $g$ la fonction définie sur $\mathrm{ℝ}$ par :

$\left\{\begin{array}{l}g\left(x\right)=\sqrt{1-x} ; x\le 1\\ g\left(x\right)=\sqrt{x^2+1} ; x>1\end{array}\right.$

1. Étudier la continuité de $g$ sur $]-\infty ;1[$ et $]1;+\infty [$

2. Étudier la continuité de $g$ en 1

3. Est-ce que $g$ est continue sur $\mathrm{ℝ}$ ?

III- Exercices

3-4/ Exercice 4

Soit $h$ une fonction numérique continue sur chacun des intervalles $]-\infty ;3[$ et $]3;+\infty [$ et dont le tableau de variations est donné par :

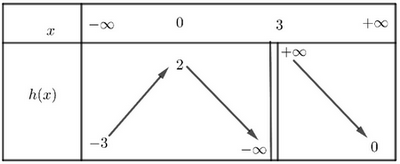
1. Déterminer les images des intervalles suivants par la fonction $h$ :

$]-\infty ;0[ ; [0;3[ ; ]-\infty ;3[ ; ]3;+\infty [$

III- Exercices

3-5/ Exercice 5

1. Justifier la continuité de chacune des fonctions suivantes sur l’intervalle $I$ :

$$\begin{gathered} \overline{)1} f\left(x\right)={\left(x^2-5\right)}^4 ; I=\mathrm{ℝ} \\ \overline{)2} f\left(x\right)=\frac{3}{x^2}-\frac{4}{x} ; I=\mathrm{ℝ}* \\ \overline{)3} f\left(x\right)={\left(\frac{3x-4}{x-1}\right)}^2 ; I=]1;+\infty [ \\ \overline{)4} f\left(x\right)=\frac{1}{\sqrt{x^2+1}} ; I=]-\infty ;0] \\ \overline{)5} f\left(x\right)=\sqrt{x^2+3} ; I=\mathrm{ℝ} \end{gathered}$$

III- Exercices

3-6/ Exercice 6

$f$ est la fonction définie sur $[-1;+\infty [$ par : $\left\{\begin{array}{l}f\left(x\right)=\frac{\sqrt{x^3+1}-3}{x-2} ; x\ne 2\\ f\left(2\right)=m\end{array}\right.$

1. Déterminer la valeur de $m$ pour que $f$ soit continue en $2$