Séance 5 - Étude d’une fonction numérique

Sommaire

I- Étude des branches infinies (Rappel)

1-1/ Les asymptotes 

1-2/ Les branches paraboliques

II- Axe de symétrie – Centre de symétrie

2-1/ Proposition 1

2-2/ Proposition 2

III- Exercices

3-1/ Exercice 1 (Étude d’une fonction polynôme)

3-2/ Exercice 2 (Étude d’une fonction rationnelle)

3-3/ Exercice 3 (Étude d’une fonction irrationnelle)

3-4/ Exercice 4

I- Étude des branches infinies (Rappel)

1-1/ Les asymptotes 

Dans tout ce qui suit, $f$ est une fonction numérique de la variable réelle $x$ et $\left({\mathcal{C}}_f\right)$ sa représentation graphique dans un repère orthonormé $\left(O,\overrightarrow{i},\overrightarrow{j}\right)$

L’asymptote horizontale

La droite d’équation $y=b$ est une asymptote horizontale de la courbe $\left({\mathcal{C}}_f\right)$ si et seulement si $\underset{x\to \pm \infty }{\lim }f\left(x\right)=b$

Exemple

I- Étude des branches infinies (Rappel)

1-1/ Les asymptotes 

L’asymptote verticale

La droite d’équation $x=a$ est une asymptote verticale de la courbe $\left({\mathcal{C}}_f\right)$ si et seulement si $\underset{x\to a}{\lim }f\left(x\right)=\pm \infty$

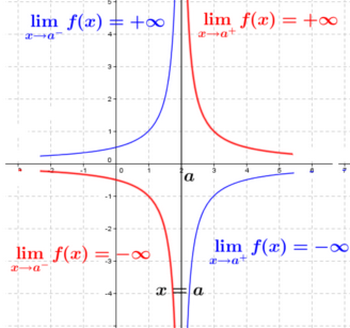
Exemple

I- Étude des branches infinies (Rappel)

1-1/ Les asymptotes 

L’asymptote oblique

La droite d’équation $y=ax+b$ est une asymptote oblique de la courbe $\left({\mathcal{C}}_f\right)$ si et seulement si $\underset{x\to \infty }{\lim }\frac{f\left(x\right)}{x}=a \left(a\ne 0\right)$ et $\underset{x\to \infty }{\lim }f\left(x\right)-ax=b$

La droite d’équation $y=ax+b$ est une asymptote oblique de la courbe $\left({\mathcal{C}}_f\right)$ si et seulement si $\underset{x\to \infty }{\lim }f\left(x\right)-\left(ax+b\right)=0$

Exemple

I- Étude des branches infinies (Rappel)

1-2/ Les branches paraboliques

Branche parabolique dirigée vers l’axe des ordonnées

Si $\underset{x\to \pm \infty }{\lim }f\left(x\right)=\pm \infty$ et $\underset{x\to \pm \infty }{\lim }\frac{f\left(x\right)}{x}=\pm \infty$ on dit que la courbe $\left({\mathcal{C}}_f\right)$ admet une branche parabolique dirigée vers l’axe des ordonnées.

Exemple

I- Étude des branches infinies (Rappel)

1-2/ Les branches paraboliques

Branche parabolique dirigée vers l’axe des abscisses

Si $\underset{x\to \pm \infty }{\lim }f\left(x\right)=\pm \infty$ et $\underset{x\to \pm \infty }{\lim }\frac{f\left(x\right)}{x}=0$ on dit que la courbe $\left({\mathcal{C}}_f\right)$ admet une branche parabolique dirigée vers l’axe des abscisses.

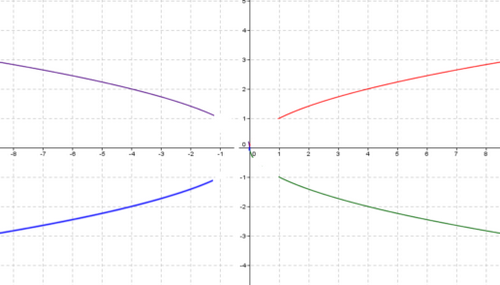
Exemple

I- Étude des branches infinies (Rappel)

1-2/ Les branches paraboliques

Branche parabolique de direction la droite d’équation $y=ax$

Si $\underset{x\to \pm \infty }{\lim }\frac{f\left(x\right)}{x}=a \left(a\ne 0\right)$ et $\underset{x\to \pm \infty }{\lim }f\left(x\right)-ax=\pm \infty$ on dit que la courbe $\left({\mathcal{C}}_f\right)$ admet une branche parabolique de direction la droite d’équation $y=ax$

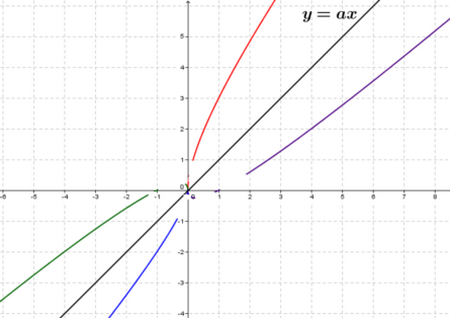
Exemple

II- Axe de symétrie – Centre de symétrie

2-1/ Proposition 1

Soit $f$ une fonction numérique et $\left({\mathcal{C}}_f\right)$ sa courbe représentative dans un repère orthogonal.

Pour que la droite $\left(D\right)$ d’équation $x=a$ soit un axe de symétrie de la courbe $\left({\mathcal{C}}_f\right)$, il suffit de montrer que pour tout$x\in D_f : \left(2a-x\right)\in D_f et f\left(2a-x\right)=f\left(x\right)$

Exemple

II- Axe de symétrie – Centre de symétrie

2-2/ Proposition 2

Soit $f$ une fonction numérique et $\left({\mathcal{C}}_f\right)$ sa courbe représentative dans un repère orthogonal.

Pour que le point $\Omega \left(a,b\right)$ soit un centre de symétrie de la courbe $\left({\mathcal{C}}_f\right)$, il suffit de montrer que pour tout $x\in D_f : \left(2a-x\right)\in D_f et f\left(2a-x\right)=2b-f\left(x\right)$

Exemple

III- Exercices

3-1/ Exercice 1 (Étude d’une fonction polynôme)

$f$ est la fonction définie par $f\left(x\right)=x^4-2x^2$

1. Donner le domaine de définition de la fonction $f$
2. Calculer $\underset{x\to +\infty }{\lim }f\left(x\right)$ et $\underset{x\to -\infty }{\lim }f\left(x\right)$
3. Étudier le comportement de la fonction $f$ au voisinage de $+\infty$ et $-\infty$
4. Donner le tableau de variation de la fonction $f$
5. Déterminer les extremums de $f$
6. Déterminer les points d’inflexions de la courbe représentant la fonction $f$
7. Déterminer les points d’intersection de la courbe représentant la fonction $f$ et $\left(ox\right)$
8. Tracer la courbe représentant la fonction $f$ dans un repère orthonormé

III- Exercices

3-2/ Exercice 2 (Étude d’une fonction rationnelle)

$f$ est la fonction définie par $f\left(x\right)=\frac{x^2+x+3}{2x^2+2x-4}$

1. Donner le domaine de définition de la fonction $f$
2.  Calculer les limites de la fonction $f$ aux bornes de son domaine de définition et donner l’interprétation graphique des résultats obtenus
3. Donner le tableau de variation de la fonction $f$
4. Tracer la courbe représentant la fonction $f$ dans un repère orthonormé
5. Montrer que la droite d’équation $x=-\frac{1}{2}$ est un axe de symétrie de la courbe représentant la fonction $f$

III- Exercices

3-3/ Exercice 3 (Étude d’une fonction irrationnelle)

$f$ est la fonction définie par $f\left(x\right)=\sqrt{x^2-4}$

1. Donner le domaine de définition de la fonction $f$
2. Calculer $\underset{x\to +\infty }{\lim }f\left(x\right)$ et $\underset{x\to -\infty }{\lim }f\left(x\right)$
3. Étudier la dérivabilité de $f$ à droite de  $2$ et à gauche de $-2$
4. Donner une interprétation géométrique des résultats de la question 3
5. Calculer la dérivée de la fonction $f$ et étudier son signe
6. Donner le tableau de variation de la fonction $f$
7. Étudier les branches infinies de la courbe $\left({\mathcal{C}}_f\right)$ représentant la fonction $f$.
8. Tracer la courbe $\left({\mathcal{C}}_f\right)$ représentant la fonction $f$ 

III- Exercices

3-4/ Exercice 4

1. Étudier la convexité de la courbe représentative de la fonction f et déterminer les points d'inflexion (s'ils existent ) dans les cas suivants :

$$\begin{gathered} \overline{)1} f\left(x\right)=\sqrt{2x-2}+x \\ \overline{)2} f\left(x\right)=\frac{1}{3}{x}^3+\frac{3}{2}{x}^2-4x+1 \\ \overline{)3} f\left(x\right)=\left(x-1\right)\sqrt{x-1} \end{gathered}$$