
Mathématiques : 2Bac Eco-SGC
Séance 2 (Continuité – Partie 1)
Professeur : Mr ETTOUHAMY Abdelhak
Sommaire
I- Continuité en un point et continuité sur un intervalle
1-1/ Continuité en un point
1-2/ Continuité à droite – Continuité à gauche
1-3/ Continuité sur un intervalle
1-4/ Les opérations sur les fonctions continues
II- Image d’un intervalle par une fonction continue
2-1/ Image d‘un intervalle
2-2/ Cas d’une fonction continue et strictement monotone
III- Exercices
3-1/ Exercice 1
3-2/ Exercice 2
3-3/ Exercice 3
3-4/ Exercice 4
3-5/ Exercice 5
3-6/ Exercice 6
I- Continuité en un point et continuité sur un intervalle
1-1/ Continuité en un point
Définition
Soit f une fonction définie sur un intervalle I et a un élément de I
f est continue en a, si limx→af(x)=f(a)
Exemples
I- Continuité en un point et continuité sur un intervalle
1-1/ Continuité en un point
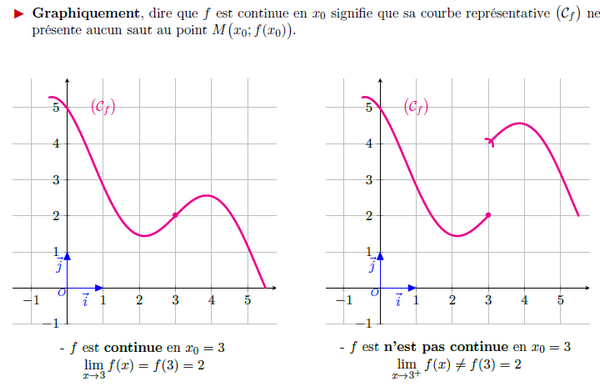
I- Continuité en un point et continuité sur un intervalle
1-2/ Continuité à droite – Continuité à gauche
Définition
- Soit f une fonction définie sur un intervalle de type [a;a+α[ avec α>0 , alors
f est continueà droite en a, si limx→a+f(x)=f(a)
- Soit f une fonction définie sur un intervalle de type ]a-α;a] avec α>0 , alors
f est continue à gauche en a, si limx→a+f(x)=f(a)
Exemple
I- Continuité en un point et continuité sur un intervalle
1-2/ Continuité à droite – Continuité à gauche
Propriété
Soit f une fonction numérique définie sur un intervalle ouvert I et a∈I.
La fonction f est continue en a si et seulement si f est continue à droite et à gauche en a.
c-à-d : limx→a-f(x)=limx→a+f(x)=f(a)
Exemple
I- Continuité en un point et continuité sur un intervalle
1-3/ Continuité sur un intervalle
Définition
f est continue sur un intervalle ouvert ]a,b[ si f est continue en tous points de cet intervalle
f est continue sur un intervalle fermé [a,b] si f est continue sur l’intervalle ouvert ]a,b[ et continue à droite en a, et à gauche en b.
I- Continuité en un point et continuité sur un intervalle
1-3/ Continuité sur un intervalle
Propriétés
Les fonctions polynômes sont continue sur ℝ.
Les fonctions rationnelles sont continues sur chaque intervalle de leur ensemble de définition.
La fonction x↦√x est continue sur [0,+∞[
Exemples
I- Continuité en un point et continuité sur un intervalle
1-3/ Continuité sur un intervalle
Remarque
- Graphiquement, une fonction est continue sur un intervalle, si on peut tracer son graphe sans lever le crayon sur cet intervalle
- Toute fonction continue sur un intervalle I, sa restriction est continue sur tout intervalle inclus dans I.
Exemple
I- Continuité en un point et continuité sur un intervalle
1-4/ Les opérations sur les fonctions continues
propriétés
Soient f et g deux fonctions continues sur un intervalle I et k∈ℝ
- Les fonctions (f+g) et (f.g) et (k.f) sont continus sur I
- Si g ne s’annule pas sur I, alors 1g et fg sont continués sur I
- Si la fonction f est continue et positive sur un intervalle I, alors la fonction √f est continue sur I.
Exemples
II- Image d’un intervalle par une fonction continue
2-1/ Image d‘un intervalle
Propriété
- Si f une fonction numérique continue sur un intervalle I, alors son image par f est un intervalle.
- Si f une fonction numérique continue sur un segment [a;b], alors son image par f est un segment [m;M],
où m et M sont, respectivements, les valeurs minimale et maximale de f sur le segment [a;b].
Géométriquement
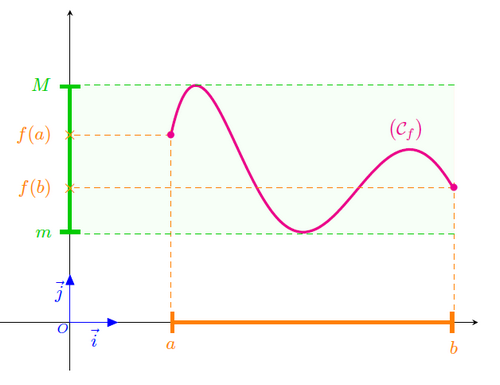
Exemple :
II- Image d’un intervalle par une fonction continue
2-2/ Cas d’une fonction continue et strictement monotone
Si f est une fonction strictement croissante :
|
L’intervalle I |
L’intervalle f(I) |
|
[a;b] |
[f(a);f(b)] |
|
[a;b[ |
[f(a);limx→b-f(x)[ |
|
]a;b] |
]limx→a+f(x);f(b)] |
|
]a;b[ |
]limx→a+f(x);limx→b-f(x)[ |
Si f est une fonction strictement décroissante :
|
L’intervalle I |
L’intervalle f(I) |
|
[a;b] |
[f(b);f(a)] |
|
[a;b[ |
]limx→b-f(x);f(a)] |
|
]a;b] |
[f(b);limx→a+f(x)[ |
|
]a;b[ |
]limx→b-f(x);limx→a+f(x)[ |
Exemple
III- Exercices
3-1/ Exercice 1
Étudier la continuité de f en a dans chaque cas :
A- {f(x)=x2-1x+1
B-
C-
III- Exercices
3-2/ Exercice 2
A- Soit la fonction définie sur par :
- Étudier la continuité de à gauche et à droite en 4
- Est-ce que est continue en 4 ?
B- Soit la fonction définie sur par :
- Étudier la continuité de en 0
III- Exercices
3-3/ Exercice 3
A- Soit la fonction définie sur par :
- Étudier la continuité de en 1
- Étudier la continuité de sur et
- Est-ce que est continue sur ?
B- Soit la fonction définie sur par :
- Étudier la continuité de sur et
- Étudier la continuité de en 1
- Est-ce que est continue sur ?
III- Exercices
3-4/ Exercice 4
Soit une fonction numérique continue sur chacun des intervalles et et dont le tableau de variations est donné par :
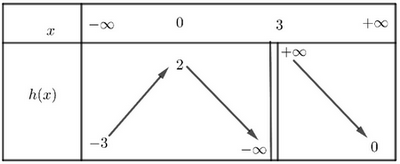
- Déterminer les images des intervalles suivants par la fonction :
III- Exercices
3-5/ Exercice 5
- Justifier la continuité de chacune des fonctions suivantes sur l’intervalle :
III- Exercices
3-6/ Exercice 6
est la fonction définie sur par :
- Déterminer la valeur de pour que soit continue en


