Séance 8 - Fonctions logarithmiques

Sommaire

I- Fonction logarithme népérienne

1-1/ Définition

1-2/ Conséquences

1-3/ Signe de ln(x)

II- Propriétés algébriques

III- Limites

3-1/ Propriétés

3-2/ Remarques

IV- Étude de la fonction $f\left(x\right)=lnx$

V- Fonction de la forme $f\left(x\right)=ln\left(u\left(x\right)\right)$

5-1/ Définition

5-2/ Vocabulaire et remarque

VI- Fonction logarithme de base a

6-1/ Définition

6-2/ Cas particuliers

6-3/ Propriétés

VII- Exercices

7-1/ Exercice 1

7-2/ Exercice 2

7-3/ Exercice 3

7-4/ Exercice 4

7-5/ Exercice 5

7-6/ Exercice 6

I- Fonction logarithme népérienne

1-1/ Définition

La fonction primitive $F$ de $f\left(x\right)=\frac{1}{x}$ sur l’intervalle $]0,+\infty [$ qui s’annule en $1 \left(F\left(1\right)=0\right)$ s’appelle la fonction logarithme népérienne

Elle est notée $F\left(x\right)=\ln \left(x\right)$ ou $F\left(x\right)=\ln x$.

Avec $F\text{'}\left(x\right)=f\left(x\right)\iff \left(\ln x\right)\text{'}=\frac{1}{x}$

Exemple

I- Fonction logarithme népérienne

1-2/ Conséquences

$\ln 1=0$

La fonction $f\left(x\right)=\ln x$ est définie sur $]0,+\infty [$.

La fonction $f\left(x\right)=\ln x$ est dérivable sur $]0,+\infty [$ (car $\left(\ln x\right)\text{'}=\frac{1}{x}$).

La fonction $f\left(x\right)=\ln x$ est continue sur $]0,+\infty [$ (car la fonction logarithme népérienne est dérivable).

La fonction $f\left(x\right)=\ln x$ est strictement croissante sur $]0,+\infty [$ (car $\left(\ln x\right)\text{'}=\frac{1}{x}>0$).

Exemple

I- Fonction logarithme népérienne

1-3/ Signe de ln(x)

Soit $x\in ]0,+\infty [$

Si : $x=1$, donc : $\ln 1=0$.

Puisque $x\to \ln \left(x\right)$ est strictement croissante sur $]0,+\infty [$

Si : $x\in ]1,+\infty [$, donc : $x>1\Rightarrow \ln x>\ln 1=0$

Si : $x\in ]0,1[$, donc : $x<1\Rightarrow \ln x<\ln 1=0$

II- Propriétés algébriques

Pour tous $a>0$ et $b>0$ et $r\in \mathrm{\mathbb{Q}}$, on a :

$$\begin{gathered} \ln ab=\ln a+\ln b \\ \ln \left(\frac{1}{a}\right)=-\ln a \\ \ln \left(\frac{a}{b}\right)=\ln a-\ln b \\ \ln a^r=r.\ln a \end{gathered}$$

Exemple

III- Limites

3-1/ Propriétés

Exemple

III- Limites

3-2/ Remarques

$\underset{x\to 0^{+}}{\lim }\ln x=-\infty$ , donc la courbe $\left({\mathcal{C}}_f\right)$ admet une asymptote verticale : c’est la droite d’équation $x=0$ (l’axe des ordonnées).

$\underset{x\to +\infty }{\lim }\ln x=+\infty$ , donc la courbe $\left({\mathcal{C}}_f\right)$ admet une branche parabolique (à déterminer ).

$\underset{x\to +\infty }{\lim }\frac{\ln x}{x}=0$ , donc la courbe  admet une branche parabolique de direction l’axe des abscisses.

IV- Étude de la fonction $f\left(x\right)=lnx$

Domaine de définition :

Continuité :

Limites :

Sens de variation de f :

V- Fonction de la forme $f\left(x\right)=ln\left(u\left(x\right)\right)$

5-1/ Définition

On pose $g\left(x\right)=\ln x$ et la fonction $u\left(x\right)$, donc : $f\left(x\right)=g\circ u\left(x\right)=g\left(u\left(x\right)\right)=\ln \left(u\left(x\right)\right)$.

Conclusion : la fonction $f\left(x\right)=\ln \left(u\left(x\right)\right)$ est la composée de deux fonctions.

Domaine de définition de f : $x\in D_f\iff \left(x\in D_u et u\left(x\right)>0\right)$.

Si de plus la fonction $u\left(x\right)$ est dérivable on a : ${\left[\ln \left(u\left(x\right)\right)\right]}^{\text{'}}=\frac{u\text{'}\left(x\right)}{u\left(x\right)}$.

De même on a : ${\left[\ln \left(\left|u\left(x\right)\right|\right)\right]}^{\text{'}}=\frac{u\text{'}\left(x\right)}{u\left(x\right)}$.

Exemple

V- Fonction de la forme $f\left(x\right)=ln\left(u\left(x\right)\right)$

5-2/ Vocabulaire et remarque

Soit $u$ une fonction dérivable sur $I$ et $\forall x\in I : u\left(x\right)\ne 0$.

La fonction $x\mapsto \frac{u\text{'}\left(x\right)}{u\left(x\right)}$ est appelée la dérivée logarithmique de la fonction $u$ sur $I$.

Puisque ${\left[\ln \left(\left|u\left(x\right)\right|\right)\right]}^{\text{'}}=\frac{u\text{'}\left(x\right)}{u\left(x\right)}$, donc les fonctions primitives de la fonction $x\mapsto \frac{u\text{'}\left(x\right)}{u\left(x\right)}$ sur $I$ sont les fonctions de la forme $F\left(x\right)=\ln \left|u\left(x\right)\right|+c$ avec $c\in \mathrm{ℝ}$.

Exemple

VI- Fonction logarithme de base a

6-1/ Définition

Soit $a\in ]0,1[\cup ]1,+\infty [$ (c.à.d. a strictement positif et différent de 1).

La fonction définie par :

$$\begin{gathered} f : ]0,+\infty [\to \mathrm{ℝ} \\ x\to f\left(x\right)=\frac{\ln \left(x\right)}{\ln \left(a\right)} \end{gathered}$$

S’appelle la fonction logarithme de base a.

On note cette fonction par $f={\log }_a$ d’où : $f\left(x\right)={\log }_a\left(x\right)$

Exemple

VI- Fonction logarithme de base a

6-2/ Cas particuliers

Cas a=e

${\log }_e\left(x\right)=\frac{\ln \left(x\right)}{\ln \left(e\right)}=\ln \left(x\right)$ ,donc le logarithme de base $e$ est le logarithme népérien.

Cas a=10

On obtient la fonction $f\left(x\right)={\log }_{10}\left(x\right)$ qui s’appelle la fonction logarithme décimale.

On note ${\log }_{10}=\log$

On a :

$$\begin{gathered} \log \left({10}^r\right)=r \\ \log \left(10\right)=1 \\ \log \left(1\right)=0 \end{gathered}$$

Exemple

VI- Fonction logarithme de base a

6-3/ Propriétés

Soit $a\in ]0,1[\cup ]1,+\infty [$ et pour tout $x,y\in ]0,+\infty [$ on a :

$$\begin{gathered} {\log }_a\left(x\times y\right)={\log }_a\left(x\right)+{\log }_a\left(y\right) \\ {\log }_a\left(\frac{1}{x}\right)=-{\log }_a\left(x\right) \\ {\log }_a\left(\frac{x}{y}\right)={\log }_a\left(x\right)-{\log }_a\left(y\right) \\ {\log }_a\left(x^r\right)=r\times {\log }_a\left(x\right) ; \left(r\in \mathrm{\mathbb{Q}}\right) \\ {\log }_a\left(\sqrt{x}\right)=\frac{1}{2}\times {\log }_a\left(x\right) \\ {\log }_a\left(\sqrt[3]{x}\right)=\frac{1}{3}\times {\log }_a\left(x\right) \end{gathered}$$

VII- Exercices

7-1/ Exercice 1

Soit la fonction $g$ définie sur $]0,+\infty [$ par $g\left(x\right)=1-\frac{1}{x^2}+\ln x$.

1. Montrer que $g\text{'}\left(x\right)=\frac{2}{x^3}+\frac{1}{x}$ pour tout $x$ de $]0,+\infty [$, et en déduire que la fonction $g$ est croissante sur $]0,+\infty [$.

2. Vérifier que $g\left(1\right)=0$, puis en déduire que $g\left(x\right)\le 0$ pour tout $x\in ]0,1]$ et $g\left(x\right)\ge 0$ pour tout $x\in [1,+\infty [$.

On considère $f$ définie sur $]0,+\infty [$ par $f\left(x\right)={\left(1+\ln x\right)}^2+\frac{1}{x^2}$.

Soit $\left({\mathcal{C}}_f\right)$ la courbe représentative de la fonction $f$ dans un repère orthonormé $\left(O,\overrightarrow{i},\overrightarrow{j}\right)$ (unité 1 cm)

3. Montrer que $\underset{x\to 0^{+}}{\lim }f\left(x\right)=+\infty$, puis interprété géométriquement ce résultat.

4. Calculer $\underset{x\to +\infty }{\lim }f\left(x\right)$.

5. Montrer que $\underset{x\to +\infty }{\lim }\frac{{\left(1+\ln x\right)}^2}{x}=0$ (on pourra poser $t=\sqrt{x}$), puis montrer que $\underset{x\to +\infty }{\lim }\frac{f\left(x\right)}{x}=0$.

6. Déterminer la branche infinie de $\left({\mathcal{C}}_f\right)$ au voisinage de $+\infty$.

7. Montrer que $f\text{'}\left(x\right)=\frac{2g\left(x\right)}{x}$ pour tout $x\in ]0,+\infty [$, puis en déduire que la fonction $f$ est décroissante sur $]0,1]$ et croissante sur $[1,+\infty [$.

8. Dresser le tableau de variations de la fonction $f$ sur $]0,+\infty [$ puis en déduire que $f\left(x\right)\ge 2$ pour tout $x\in ]0,+\infty [$.

9. Construire la courbe $\left({\mathcal{C}}_f\right)$ de $f$ dans le repère orthonormé $\left(O,\overrightarrow{i},\overrightarrow{j}\right)$ (on admettra que la courbe de $f$ possède un seul point d’inflexion, on ne le déterminera pas).

VII- Exercices

7-2/ Exercice 2

Soit la fonction $g$ définie sur $]0,+\infty [$ par $g\left(x\right)=\frac{2}{x}-1+2\ln x$.

On considère le tableau de variations de la fonction $g$ sur $]0,+\infty [$ :

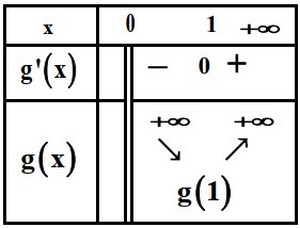
1. Calculer $g\left(1\right)$.

2. En déduire à partir du tableau que $g\left(x\right)>0$ pour tout $x\in ]0,+\infty [$.

On considère $f$ définie sur $]0,+\infty [$ par $f\left(x\right)=3-3x+2\left(x+1\right)\ln x$.

Soit $\left({\mathcal{C}}_f\right)$ la courbe représentative de la fonction $f$ dans un repère orthonormé $\left(O,\overrightarrow{i},\overrightarrow{j}\right)$ (unité 2 cm)

3. Montrer que $\underset{x\to 0^{+}}{\lim }f\left(x\right)=-\infty$, et interpréter géométriquement ce résultat.

4. Montrer que $\underset{x\to +\infty }{\lim }f\left(x\right)=+\infty$ (pour le calcul de la limite on pourra utiliser l’écriture suivante $f\left(x\right)=x\left[\frac{3}{x}-3+2\left(1+\frac{1}{x}\right)\ln x\right]$)

5. Montrer que la courbe $\left({\mathcal{C}}_f\right)$ admet au voisinage de $+\infty$ une branche parabolique dont la direction
   est celle de l’axe des ordonnées.

6. Montrer que $f\text{'}\left(x\right)=g\left(x\right)$ pour tout $x\in ]0,+\infty [$.

7. En déduire que la fonction $f$ est strictement croissante sur $]0,+\infty [$, et dresser le tableau de variations de la fonction $f$ sur $]0,+\infty [$.

8. Montrer que $I\left(0,1\right)$ est un point d’inflexion de la courbe $\left({\mathcal{C}}_f\right)$.

9. Montrer que $y=x$ est l’équation de la droite $\left(T\right)$ tangente à la courbe $\left({\mathcal{C}}_f\right)$ au point $I$.

10. Construire dans le même repère $\left(O,\overrightarrow{i},\overrightarrow{j}\right)$ la droite $\left(T\right)$ et la courbe $\left({\mathcal{C}}_f\right)$.

VII- Exercices

7-3/ Exercice 3

Soit la fonction $g$ définie sur $]0,+\infty [$ par $g\left(x\right)=x\left(x-1\right)+\ln x$.

1. Calculer $g\text{'}\left(x\right)$ pour tout $x\in ]0,+\infty [$.

2. Étudier les variations de la fonction $g$.

3. Calculer $g\left(1\right)$, puis déduire le signe de $g\left(x\right)$ sur $]0,+\infty [$.

Soit $f$ la fonction définie sur $]0,+\infty [$ par $f\left(x\right)={\left(x-1\right)}^2+{\ln }^2\left(x\right)$.

Soit $\left({\mathcal{C}}_f\right)$ la courbe représentative de la fonction $f$ dans un repère orthonormé $\left(O,\overrightarrow{i},\overrightarrow{j}\right)$ (unité 1 cm)

4. Calculer $\underset{x\to 0^{+}}{\lim }f\left(x\right)$, et interpréter le résultat géométriquement.

5. Calculer $\underset{x\to +\infty }{\lim }f\left(x\right)$ et $\underset{x\to +\infty }{\lim }\frac{f\left(x\right)}{x}$, puis étudier la branche infinie de la courbe $\left({\mathcal{C}}_f\right)$ au voisinage de $+\infty$.

6. Montrer que $\forall x\in ]0,+\infty [ : f\text{'}\left(x\right)=\frac{2g\left(x\right)}{x}$.

7. En déduire les variations de $f$ sur $D_f$.

8. Tracer $\left({\mathcal{C}}_f\right)$ dans un repère orthonormé $\left(O,\overrightarrow{i},\overrightarrow{j}\right)$.

Soit $h$ la restriction de $f$ à l'intervalle $I=]0,1]$.

9. Montrer que la fonction $h$ admet une fonction réciproque $h^{-1}$ définie sur un intervalle $J$ à déterminer.

10. Tracer $\left({\mathcal{C}}_{h^{-1}}\right)$ dans le repère $\left(O,\overrightarrow{i},\overrightarrow{j}\right)$.

VII- Exercices

7-4/ Exercice 4

Partie 1

Soit $g$ la fonction numérique définie sur $]0,+\infty [$ par : $g\left(x\right)=x^2+x-2+2\ln x$

1. Vérifier que $g\left(1\right)=0$.

Soit le tableau de variations de la fonction $g$ :

2. Montrer que $g\left(x\right)\le 0$ pour tout $x\in ]0;1]$, et que $g\left(x\right)\ge 0$  pour tout $x\in [1;+\infty [$.

Partie 2

On considère la fonction $f$ définie sur $]0,+\infty [$ par :

$f\left(x\right)=x+\left(1-\frac{2}{x}\right)\ln x$

Et soit ${\mathcal{C}}_f$ sa courbe représentative dans un repère orthonormé $(0;\overrightarrow{i};\overrightarrow{j})$. (Unité : 1cm)

1. Calculer $\underset{x\to 0^{+}}{\lim }f\left(x\right)$ et interpréter graphiquement le résultat obtenu.

2. Montrer que : $\underset{x\to +\infty }{\lim }f\left(x\right)=+\infty$

3. Montrer que la courbe ${\mathcal{C}}_f$ admet au voisinage de $+\infty$ une branche parabolique de direction la droite $\left(D\right)$ d'équation $y=x$.

4. Montrer que : $\left(\forall x\in ]0,+\infty [\right) : f\text{'}\left(x\right)=\frac{g\left(x\right)}{x^2}$

5. En déduire que la fonction $f$ est décroissante sur l’intervalle $]0;1]$ et croissante sur $[1;+\infty [$.

6. Dresser le tableau de variations de $f$ sur $[1;+\infty [$.

7. Résoudre dans l'intervalle $]0,+\infty [$ l'équation $\left(1-\frac{2}{x}\right)\ln x=0$.

8. En déduire que ${\mathcal{C}}_f$ coupe la droite $\left(D\right)$ en deux points dont on déterminera les coordonnées,

9. Montrer quo pour tout $x\in \left[1;2\right] : f\left(x\right)\le x$, et on déduire la position relative de la courbe $\left(D\right)$ par rapport à la droite sur l'intervalle $\left[1;2\right]$.

10. Construire $\left(D\right)$ et ${\mathcal{C}}_f$ dans le repère $(0;\overrightarrow{i};\overrightarrow{j})$.

(On admet que ${\mathcal{C}}_f$ possède un seul point d'inflexion dont l’abscisse est comprise entre $2,4$ et $2,5$).

VII- Exercices

7-5/ Exercice 5

On considère $f$ définie sur $[1,+\infty [$ par $f\left(x\right)=x\sqrt{\ln x}$.

Soit $\left({\mathcal{C}}_f\right)$ la courbe représentative de la fonction $f$ dans un repère orthonormé $\left(O,\overrightarrow{i},\overrightarrow{j}\right)$.

1. Montrer que $f$ est continue sur $[1,+\infty [$.

2. Étudier la dérivabilité de $f$ à droite en $1$, et interpréter géométriquement le résultat trouvé.

3. Dresser le tableau de variation de $f$.

4. Déterminer l’intersection de $\left({\mathcal{C}}_f\right)$ et $\left(\Delta \right): y=x$.

5. Tracer $\left({\mathcal{C}}_f\right)$ et $\left(\Delta \right)$ dans le repère $\left(O,\overrightarrow{i},\overrightarrow{j}\right)$.

6. Montrer que $f$ admet une fonction réciproque $g$ définie sur $J=[0;+\infty [$.

On considère la suite $\left(u_n\right)$ définie par $u_0=0$ et $u_{n+1}=g\left(u_n\right)$ pour tout $n$ de $\mathrm{\mathbb{N}}$.

7. Montrer que pour tout $n$ de $\mathrm{\mathbb{N}}$, on a : $0\le u_n\le e$

8. Montrer que la suite $\left(u_n\right)$ est décroissante.

9. En déduire que $\left(u_n\right)$ est convergente et trouver sa limite.

VII- Exercices

7-6/ Exercice 6

Partie 1

Soit $g$ la fonction définie sur $]-1;+\infty [$ par : $g\left(x\right)=\frac{2x}{x+1}-\ln \left(1+x\right)$

1. Dresser le tableau de variation de $g$.

2. Montrer que l’équation $g\left(x\right)=0$ admet dans l’intervalle $]-1,+\infty [$ deux solutions $0$ et $\alpha$, et vérifier que $3,8<\alpha <4$.

3. En déduire le signe de $g\left(x\right)$ pour tout $x\in ]-1;+\infty [$.

4. Montrer que pour tout $x\in ]-1;+\infty [$, on a $g\left(x\right)\le 1$.

Partie 2

Soit $f$ la fonction définie sur $[0;+\infty [$ par $f\left(x\right)=\frac{\ln \left(1+x\right)}{\sqrt{x}}$ si $x>0$ et $f\left(0\right)=0$.

On désigne par $\left({\mathcal{C}}_f\right)$ la courbe représentative de $f$ dans un repère orthonormé $\left(O,\overrightarrow{i},\overrightarrow{j}\right)$ du plan.

1. Montrer que $f$ est continue sur $[0;+\infty [$.

2. Étudier la dérivabilité de $f$ à droite en $0$.

3. Montrer que : $\left(\forall x>0\right): f\text{'}\left(x\right)=\frac{g\left(x\right)}{2x\sqrt{x}}$

4. Dresser le tableau de variation de $f$.

5. Vérifier que $f\left(\alpha \right)=\frac{2\sqrt{\alpha }}{1+\alpha }$.

6. Tracer la courbe $\left({\mathcal{C}}_f\right)$ dans le repère $\left(O,\overrightarrow{i},\overrightarrow{j}\right)$.