
Mathématiques : 2 Bac SPC-SVT-STE-STM
Séance 3 (Continuité – Partie 2)
Professeur : Mr CHEDDADI Haitam
Sommaire
I- Théorème des valeurs intermédiaires
1-1/ Propriété (Théorème des valeurs intermédiaires)
1-2/ Conséquences
II- Fonction réciproque d’une fonction continue et strictement monotone sur un intervalle I
2-1/ Théorème
2-2/ Relation entre f et sa réciproque f-1
2-3/ Propriétés de la fonction réciproque f-1
III- La fonction racine d’ordre n (ou racine nième)
3-1/ Définition et théorème
3-2/ Cas particuliers
3-3/ Propriétés
3-4/ Limites de la fonction g(x)=n√f(x)
VI- Puissance rationnelle d’un nombre réel positif
4-1/ Définition
4-2/ Propriétés
V- Exercices
5-1/ Exercice 1
5-2/ Exercice 2
5-3/ Exercice 3
5-4/ Exercice 4
5-5/ Exercice 5
5-6/ Exercice 6
I- Théorème des valeurs intermédiaires
1-1/ Propriété (Théorème des valeurs intermédiaires)
f est une fonction continue sur [a,b].
Pour tout nombre k compris entre f(a) et f(b), il existe au moins un élément c de [a,b] tel que f(c)=k
1-2/ Conséquences
Puisque la fonction f est continue on a f([a,b])=[m,M] (l’image d’un segment est un segment).
Si f est continue sur [a,b] et f(a)f(b)<0 alors l’équation f(x)=0 admet au moins une solution c dans ]a,b[.
Exemples
1-3/ Cas d’une fonction continue et monotone
f est une fonction continue et strictement monotone sur [a,b].
Pour tout nombre k compris entre f(a) et f(b), il existe un seul un élément c de [a,b] tel que f(c)=k
II- Fonction réciproque d’une fonction continue et strictement monotone sur un intervalle I
2-1/ Théorème
Toute fonction continue et strictement monotone sur I , admet une fonction réciproque définie sur f(I)
f:I↦J est une fonction si tout x∈I a une et seule image y∈J et de même si tout y∈J a un et seul antécédent x∈I
On définie une autre fonction notée f-1 et appelée fonction réciproque de f avec :
f:I↦J=f(I) x↦f(x)=y et f-1:J=f(I)↦I y↦f-1(y)=x
Exemples
II- Fonction réciproque d’une fonction continue et strictement monotone sur un intervalle I
2-2/ Relation entre f et sa réciproque f-1
{f(x)=yx∈I⇔{f-1(y)=xy∈J
et
∀x∈I : f-1of(x)=x
et
{∀y∈J : fof-1(y)=y∀x∈I : f-1of(x)=x
Exemples
II- Fonction réciproque d’une fonction continue et strictement monotone sur un intervalle I
2-3/ Propriétés de la fonction réciproque f-1
La fonction réciproque f-1 est continue sur J=f(I)
La fonction réciproque f-1 et f varient dans le même sens.
(Cf) et (Cf-1) sont symétriques par rapport à la 1er bissectrice ((D):y=x)
Exemples
III- La fonction racine d’ordre n (ou racine nième)
3-1/ Définition et théorème
La fonction f(x)=xn (avec n∈ℕ*) est continue et strictement croissante sur [0,+∞[
Sa fonction réciproque f-1 sera notée f-1(x)=n√x=x1n et appelée La fonction racine d’ordre n (ou la fonction racine nième)
On l’appelle n√x la racine d’ordre n du réel positif x
3-2/ Cas particuliers
Cas n=1 on a f-1(x)=1√x=x (pas d'importance). Donc on prend n∈ℕ-{0,1}
Cas n=2 on a f-1(x)=2√x=√x (racine carrée)
Cas n=3 on a f-1(x)=3√x (racine cubique ou racine d’ordre 3)
III- La fonction racine d’ordre n (ou racine nième)
3-3/ Propriétés

III- La fonction racine d’ordre n (ou racine nième)
3-4/ Limites de la fonction g(x)=n√f(x)
limx→x0f(x)=+∞⇒limx→x0n√f(x)=+∞
et
limx→x0f(x)=l et l≥0⇒limx→x0n√f(x)=n√l
Les deux propriétés restent vraies si on remplace x→x0 par x→x0- ou x→x0+ ou x→x+∞
Exemples
VI- Puissance rationnelle d’un nombre réel positif
4-1/ Définition
x∈ℝ+* et n∈ℕ* et m∈ℤ
On pose r=mn∈ℚ
Le nombre n√xm son écriture sera de la façon suivante n√xm=xmn ou encore par n√xm=xr
xr est appelé puissance rationnelle du nombre réel positif x d’exposant r
(0r=0 ; r≠0)
Exemples
VI- Puissance rationnelle d’un nombre réel positif
4-2/ Propriétés
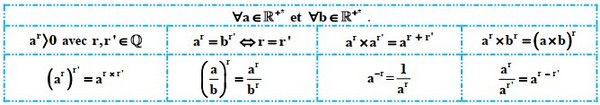
Exemples
V- Exercices
5-1/ Exercice 1
Soit f la fonction numérique définie sur ℝ par: f(x)=x6+2x4-1.
- Montrer que l’équation x6+2x4-1=0 admet au moins une solution sur ]0;1[.
On considère la fonction g définie sur ℝ par: g(x)=x3-6x2+9x+1.
- Dresser le tableau de variaton de g sur ℝ.
- Montrer que l’équation g(x)=0 admet une unique solution sur ℝ. On note cette solution par α.
- Déterminer le signe de g(x) sur [1;+∞[ .
V- Exercices
5-2/ Exercice 2
On considère la fonction f définie par: f(x)=x2x+1.
- Déterminer Df, puis calculer les limites de f aux bornes de Df.
- Montrer que: (∀x∈Df) f'.
- Dresser le tableau de variation de .
- Déterminer .
Soit la restriction de sur l’intervalle .
- Montrer que admet une fonction réciproque définie sur un intervalle que l’on déterminera.
- Monter que : .
V- Exercices
5-3/ Exercice 3
- Calculer les limites suivantes :
1-
2-
3-
4-
5-
6-
V- Exercices
5-4/ Exercice 4
Soit la fonction définie sur par :
- Montrer que: .
- Montrer que est continue sur l’intervalle .
- Montrer que .
- Déduire les variations de sur .
Soit la restriction de sur .
- Montrer que admet une fonction réciproque définie sur un interval à déterminer.
- Montrer que .
- Déduire .
V- Exercices
5-5/ Exercice 5
On considère la fonction définie sur par: .
- Montrer que est strictement croissante sur .
- Montrer que l’équation admet une solution unique dans .
- Calculer , puis déduire un encadrement de d’amplitude .
- Montrer que
V- Exercices
5-6/ Exercice 6
On considère la fonction définie par : .
- Justifier que .
- Calculer les limites de aux ornes de .
- Montrer que est continue et strictement décroissante sur .
- Montrer que l'équation admet une solution unique dans .
- Vérifier que .


